Практичне заняття 2
Спеціальні типи перетворення фур'є . Віконне перетворення фур'є
Мета
надати практичні навички представлення ШПФ.
надати практичні навички представлення віконного перетворення Фур'є.
надати представлення безперевного перетворення Фур'є.
2.1. Дискретний Фур'є-аналіз і спектр періодичних функцій.
Припустимо,
що деяка функція (сигнал) задана рядом
рівновіддалених дискретних звітів з
числом
,
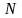тобто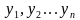
.
У цьому випадку у нас немає ніяких
підстав вважати, що в проміжках між
вузлами значення функції непостійні.
Якщо вони постійні, то інтеграли при
розрахунку коефіцієнтів Фур'є можуть
обчислюватися найпростішим методом
прямокутників:
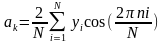і
(2.1)
Наведені формули для коефіцієнтів Фур'є є єдиним і теоретично обґрунтованими формулами наближеного обчислення коефіцієнтів Фур'є. Для довільних функцій вони забезпечують мінімум середньоквадратичної похибки.
При
дискретному завданні функції (сигналу)
постає питання про те, яке число гармонік
(
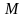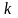від
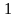до
)
може представляти сигнал? Або, навпаки,
при заданому числі гармонік, яке число
відліків
допустимо? Відповідь на це питання дає
теорема Котельникова: число відліків
повинно мінімум вдвічі перевищувати
число гармонік, на найвищу точку гармоніки
спектра в ідеалі достатньо мати два
відліки.
Завдання 2.1.
В
Mathcad
провести
стандартний дискретний спектральний
аналіз і синтез вектора
,
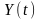при:
частоті
і числі гармонік
Рішення:
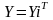
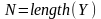
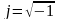
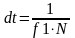
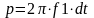
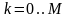
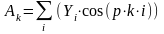
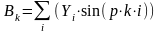
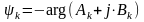
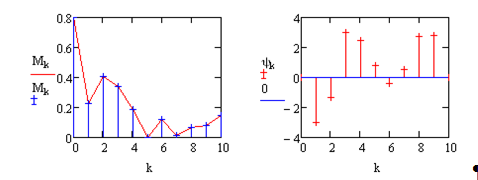
Рис. 2.1. Стандартний дискретний спектральний аналіз і синтез.
Залежність амплітуд і фаз гармонік від частоти, отримали назву амплітудного і фазового спектру сигналу. Для періодичних коливань такий спектр є дискретним. Його зручно представляти вертикальними відрізками прямих, довжина яких, визначає значення амплітуди і фази тієї чи іншої гармоніки. На амплітудному спектрі представлена огинаюча спектра.
2.2 Гармонічний синтез дискретного заданого сигналу.
Завдання 2.2.
Реалізувати Фур'є-синтез попереднього сигналу по представленій формулі. Вона більш зручна, оскільки вимагає вдвічі меншого числа обчисленої тригонометричної функції косинуса. При:
Рішення:
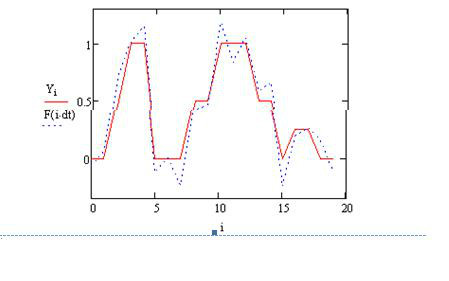
Рис. 2.2. Стандартний дискретний спектральний аналіз і синтез.
На
Рис. 2.2. представлені графіки початкового
сигналу і результат його синтезу по 20
гармонікам. В даному випадку заданий
досить складний сигнал. Чітко видно
сильний прояв ефекту Гіббса, пов'язаний
з обмеженим числом гармонік
.
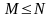В результаті стандартного синтезу дискретного сигналу ми отримуємо вже не дискретне, а безперервне представлення сигналу рядом Фур'є з числом гармонік . Через вже не раз зазначеного ефекту Гіббса тригонометрична апроксимація та інтерполяція сигналу має досить низьку точність. Підвищення точності можливо за рахунок різкого збільшення числа відліків (і гармонік при синтезі) - нерідко до багатьох сотень і тисяч. Але, в цьому випадку ми зіткнемося з повною непридатністю описаного методу аналізу і синтезу, пов'язаної з неприпустимо великими тимчасовими витратами на обчислення.
2.3. Безперервне перетворення Фур'є.
Якщо
функція чи сигнал визначені на деякому
кінцевому проміжку простору або часу,
то вважаємо сигналперіодичним і
застосовуємо до нього описаний вище
спектральний аналіз і синтез. Наприклад,
якщо сигнал визначений на деякому
проміжку часу
,
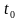то його можна порахувати періодичним
з періодом
або частотою
.
Інший
шлях полягає в переході до безперервного
перетворення Фур'є в загальному вигляді
- для довільного сигналу. Пряме перетворення
Фур'є в такому вигляді дозволяє отримати
в аналітичному вигляді функцію частоти
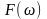від тимчасової функції
.
Воно реалізується формулою:
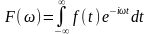(2.2)
-
скалярна функція незалежної змінної
.
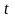Оскільки ми виходимо з пропозиції, що
у
загальному неперіодична функція, то
вже не можна вести мову про окремі
гармоніки і про дискретний спектр
сигналу. Спектр
стає
безперервним і можна говорити лише про
щільності енергії сигналу в деякій
малій (наближається до нуля) смузі
частот. Так що в даному випадку
є
залежність густини енергії сигналу від
частоти.
Зворотне перетворення Фур'є задається наступним чином:
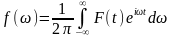(2.3)
Ця формула дозволяє по функції знайти в аналітичному вигляді функцію .
З формули (2.2) випливає головний недолік прямого перетворення Фур'є: інтегральна оцінка всіх частотних складових спектра незалежно від часу їх існування. Це пов'язано безпосередньо з нескінченними межами інтегрування. У результаті цілком можливі випадки, коли зовсім різні сигнали мають однаковий частотний спектр. Фур'є-аналіз прекрасно підходить для стаціонарних сигналів.
Завдання 2.3.
Необхідно
реалізувати нестаціонарний сигнал ( в
Mathcad),
у якого певні частотні компоненти
існують тільки в певні проміжки часу
або коли параметри сигналу змінюються
в часі. Реалізується це за допомогою
функцій символьного процесора
і
.
Рішення:
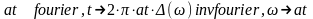
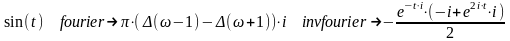
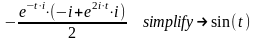
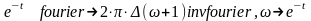
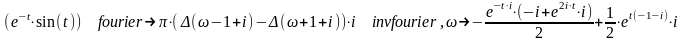
У
випадку функції синуса Mathcad теж впорався
із завданням, але привів добре відомий
вислів для синуса, представлене через
експоненціальні функції. Його вдалося
перетворити в звичайний за допомогою
функції спрощення символьних результатів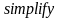
.
Для ряду функцій пряме перетворення
Фур'є дає уявлення, що містить функцію
Дірака Dirac
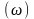.Співвідношення
(2.2) і (2.3) носять фундаментальний
теоретичний характер, ніж практичний.
Це видно в наших прикладах хоча б з того,
що ми не можемо побудувати графік функції
і
обчислити її значення.
У
зв'язку з цим на практиці зручніше
застосовувати вже згаданий підхід:
періодизацію обмежених у часі сигналів.
Тим більше у зв'язку з тим, що інтегрування
в межах від
до
зустрічається
великі і часом непереборні труднощі.