Недоопределённые системы

Рассмотрим системы с количеством уравнений меньшим количества неизвестных. Такие системы имеют либо бесконечное множество решений, либо не имеют решения вовсе.

Решим аналитически систему двух уравнений с тремя неизвестными при помощи символьного процессора.

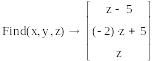
Но для решения недоопределённых систем, состоящих из большего числа уравнений, необходимо использовать численные алгоритмы.

Необходимо выделить из бесконечного множества решений одно, обоснованное математически решение. Эта проблема решается с посредством привлечения понятия нормального псевдорешения.

Физический смысл заключается в том, что проведено m измерений с n неизвестными. Для того, чтобы получить единственное разумное решение, необходимо доопределить задачу, добавив априорную информацию о векторе х. Если подобная информация отсутствует, то решить систему невозможно. Следует ввести в задачу определённые ожидания о величине вектора х. Математически можно полагать вектор х нулевым, так как от любого вектора перейти к нулевому вектору можно линейным преобразованием.

Таким образом, вполне логично объявить решением недоопределённой системы такое решение, которое ближе всех находится к нулевому вектору, т.е. обладает минимальной нормой |x|-min. Это решение называют нормальным псевдорешением системы

Пример:

Найти нормальное псевдорешение недоопределённый системы уравнений.

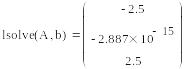
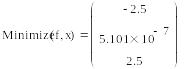
Вырожденные системы линейных уравнений

Вырожденная система- это система, описываемая матрицей с нулевым определителем (сингулярной матрицей).

Плохо обусловленная система –определитель А не равен 0, но число обусловленности очень велико.

Для решения таких систем разработан очень эффективный приём, называемый регуляризацией.

Регуляризация

Рассмотрим  метод регуляризации, предложенный Тихоновым для решения обратных задач на примере линейной задачи. Как известно, она ставится в форме решения плохо обусловленной системы М линейных уравнений: (1) с неизвестным вектором N^J, подлежащим определению (по повторяющимся индексам здесь и далее мы предполагаем суммирование). Алгоритм построения матрицы А и конкретный вид вектора правых частей уравнений f выражают физическую постановку задачи. В частности, задача томографии состоит в численном решении системы большого числа интегральных уравнений, дискретизация который приводит к  системе линейных уравнений с матрицей А и правыми частями f, выражающими результаты измерений. Система (1) может быть переопределённой, т.е. количество уравнений может превышать (часто в несколько десятков раз) число неизвестных.  Поскольку матрица А является плохо обусловленной, то точное решение (1) (в смысле псевдорешения) оказывается крайне неустойчивым и, как правило, весьма далёким от правильного. Общеупотребительный подход к решению некорректных задач заключается в их регуляризации. При этом используется дополнительная априорная информация о решении, которая может быть как качественной, так и количественной. Например можно искать решение, максимально близкое к некоторому профилю , т.е. к некоторому вектору  N₀. Концепция регуляризации применительно к (1) сводится к замене задачи на поиск псевдорешения на задачу о минимизации следующего функционала:

, (2) где  a - малый положительный параметр регуляризации, который необходимо

подобрать определенным способом.  Задача о минимизации функционала (2) для системы линейных алгебраических уравнений (1) эквивалентна системе, содержащей M линейных уравнений:  , (3) где символ E обозначает единичную матрицу размера MхM. Решая систему (3), можно получить регуляризованное решение, зависящее от a. Из (3) хорошо ясен смысл параметра a: при малых a~0 обусловленность системы (3) близка к плохой обусловленности (1), а при больших a система (3) обусловлена хорошо, но её решение далеко от решения исходной обратной задачи. А именно, чем больше параметр регуляризации, тем ближе решение к N₀. Очевидно, что на практике необходимо выбирать промежуточные a. Описанный регуляризационный подход сводит некорректную задачу  к условно-корректной (по Тихонову) задаче отыскания решения системы (3), которое, в силу линейности задачи, является единственным и устойчивым. Заметим, что метод регуляризации успешно применяется и для решения нелинейных некорректных обратных задач. Однако в этом случае заменить задачу минимизации функционала (2) линейной системой типа (3) невозможно. С вычислительной точки зрения, это означает, что вместо задачи решения системы алгебраических линейных уравнений придется численно решать задачу на глобальный экстремум функции, которая часто более сложна (в частности, из-за возможного наличия в нелинейном случае многих локальных минимумов). Пример регуляризации

Покажем на конкретном примере задачи геофизической томографии, как решаются при помощи регуляризации линейные обратные задачи. Наиболее типичная постановка задачи  томографии состоит в том, чтобы по набору измерений каждого из имеющихся приёмников в каждый момент времени измерений восстановить в узлах сетки, которой покрывается объект, поле пространственных переменных (которыми может быть, к примеру, температура в атмосфере или океане, скорость ветра и т.п.) . Для окончательной формулировки вычислительной задачи необходимо записать систему линейных уравнений в дискретном виде. 

Как показано выше, концепция  применительно к  рассматриваемой линейной задаче томографии, сводится к ее замене на систему линейных алгебраических уравнений, зависящей от параметра регуляризации a:  (*) .

Проиллюстрируем сказанное конкретным вычислительным примером. Зададим некоторую двумерную модель пространственного поля (например, скорости ветра  в атмосфере или электронной концентрации в ионосфере), которое образована наложением на регулярный высотный профиль неоднородности, расположенной в центре (рис.1), и промоделируем процесс доплеровских измерений, который соответствует схеме дистанционного зондирования атмосферы с передатчиком на борту перемещающегося ИСЗ и приемниками на поверхности Земли. 

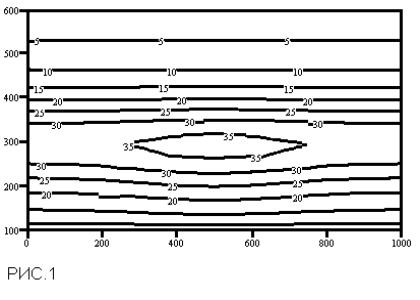
Высота ИСЗ в компьютерном эксперименте составляла 900 км, два приёмника располагались в точках с координатами 0 км и 500 км по поверхности Земли в плоскости пролёта ИСЗ. Дискретизация интегральных уравнений проводилась  методом кусочно-планарной аппроксимации на сетке 21х21 узел. Такая крупная (по сравнению с реальными задачами томографии атмосферы) сетка была взята нами для того, чтобы проверить выдвигаемую методику с помощью точного метода решения системы линейных уравнений (*), не прибегая к приближённым итерационным алгоритмам. Поскольку число арифметических операций, требующихся компьютеру для завершения точного метода, порядка (M)⁶ , то для расчёта на сетке 100х100 узлов необходимо время в 15,000 раз большее. В скобках заметим, что на выполнение программы решения системы (*) методом Гаусса с выбором главного элемента занимает на Pentium-200 время порядка минуты, поэтому на практике следует, конечно, использовать итерационные методы. Эффективным может оказаться, например, метод сопряжённых градиентов, поскольку в его рамках можно организовать эффективный спуск по параметру регуляризации. Задав реалистичный высотный профиль N₀(z), проиллюстрируем предложенный подход, рассчитав точное решение регуляризованной задачи. Для того, чтобы определить оптимальный параметр регуляризации, проведём серию расчётов с различными , контролируя невязку. На рис.2 изображена зависимость нормы невязки  решения регуляризованной задачи от параметра регуляризации. На том же рисунке изображена суммарная ошибка (т.е. норма отклонения решения от модельного распределения).

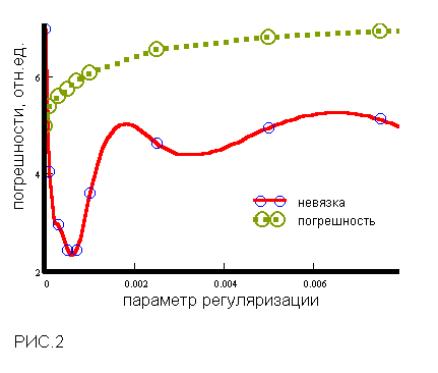Для реконструкции можно использовать значение a, соответствующее глобальному минимуму зависимости e(a) (рис.3), либо применить т.н. принцип невязки, который требует выбора a, с которым невязка приблизительно равна сумме погрешностей измерений (т.е. заданий правой части) и аппроксимации (результат реконструкции изображён на рис.4). Из сравнения четырёх полей видно, что наилучшее совпадение с моделью демонстрирует последний рисунок.

 

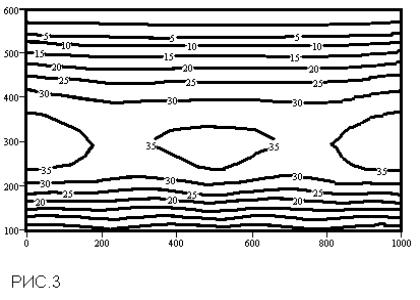
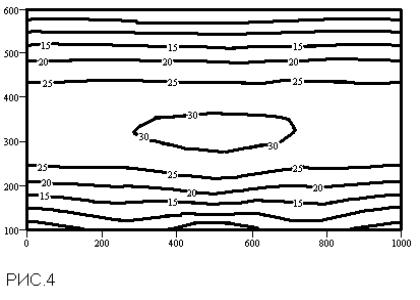
Пример:

Дана вырожденная матрица. Найти её решения в зависимости от параметра регуляризации λ. При параметре регуляризации, равным 0, система не имеет решений.

На первом этапе проводим регуляризацию матрицы.

На втором выбираем оптимальное λ. Можно выбрать норму невязки, равной априорной оценке погрешностей задания исходных данных, либо использовать квазиоптимальный метод.