Переопределённые системы
Рассмотрим систему уравнений, в которой число уравнений больше, чем число неизвестных, т.е. матрица А – прямоугольная. Чаще всего такие системы не имеют решений, т.е. являются несовместными или переопределёнными. Несовместные системы не могут быть решены с помощью вычислительного блока Given/Find.
Пример:
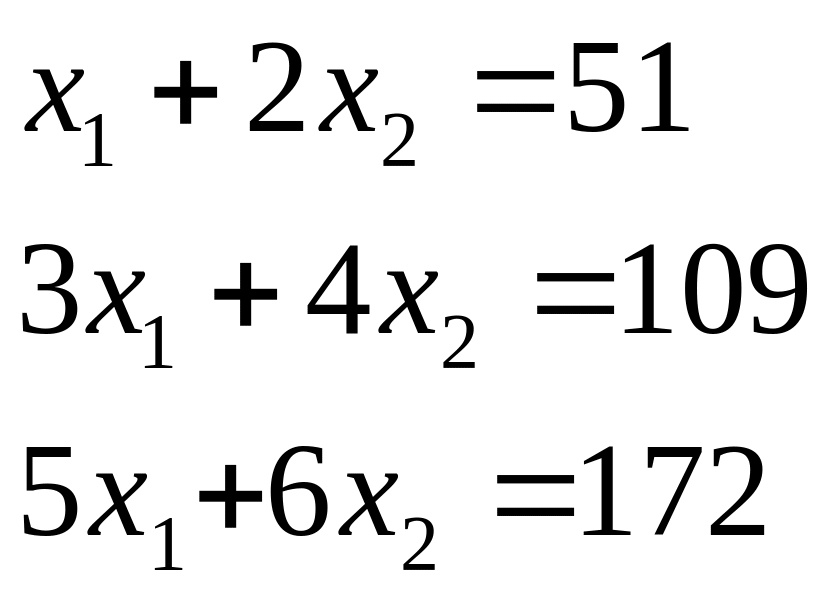Попытаемся
решить систему уравнений:
Через оператор присваивания вводим матрицу коэффициентов и вектор свободных членов.
Решаем данную систему методом Гаусса
Вводим приблизительные решения корней в вектор х
Включаем вычислительный блок
Записываем
а*х=в
Находим корни Find(x)=
Mathcad выдаст ошибку.
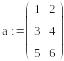
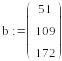
В редких случаях система с прямоугольной матрицей может оказаться совместной (если выбран соответствующий вектор b).
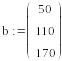Пример:
На практике задачи отыскания решения переопределённых систем линейных уравнений встречаются довольно часто. Точного решения такой системы не найти.
Рассмотрим математическую постановку задач решения систем с прямоугольной матрицей. Вместо точного решения следует организовать поиск такого вектора х, который будет наилучшим образом удовлетворять всем уравнениям, т.е. минимизировать их невязку (расхождение между вектором А*х и вектором свободных членов b). Так как невязка A*x-b является векторной величиной, то минимизации надо подвергать её норму (т.е. скаляр) |A*x-b|.
Т.е. принято искать не точное решение (которого просто нет), а псевдорешение-вектор, минимизирующий норму невязки системы уравнений. Задача решения линейной системы уравнения заменяется задачей отыскания глобального минимума функции f(x)=|A*x-b|. Поскольку эта минимизируемая норма зависит от суммы квадратов компонент неизвестного вектора, то процедура поиска псевдорешения является реализацией метода наименьших квадратов.
Для решения задач минимизации невязки системы уравнений в Mathcad предусмотрены две встроенные функции Minerr и Minimize.
Если используется функция Minerr, то используется ключевое слово Given, а в первом случае явно определяется функция f(x), подлежащая минимизации.
1-й
способ:
2-й способ:
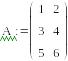
Во-первых, сравнивая результаты, можно обнаружить, что они абсолютно различны, причём более похож на правильный ответ, выдаваемый функцией Minimize. Разгадка заключается в особенностях применения численного алгоритма, заложенного в функцию MinErr. Алгоритм заложен линейный, тип алгоритма можно изменить по правой кнопке мыши. Установить на нелинейный, выбрать метод из трёх предложенных.
Во-вторых, приближённое решение c использованием Given невозможно при наличии дополнительных условий, выражающих вспомогательную априорную информацию о постановке задачи. В результате исходная задача сводится к условной минимизации функции f(x) c использованием дополнительных неравенств.
Пример:
Поиск псевдорешения при наличии априорной информации
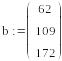
При выборе нелинейного алгоритма появляются отрицательные ответы, а при добавлении дополнительных условий в задачу решения ещё раз меняются.