Решение слау с использованием вычислительного блока Given/Find

Дана система линейных уравнений. Найти её решение.

3x + 2x + x + 11x = 25

7x + 4x + 3x + 5x =37

x + 10x + 2x + 19x = 44

6x - 8x + 14x + 15x = 31

Алгоритм выполнения:

1. Ввести начальные значения корней

2. Ввести ключевое слово Given

3. Через логическое равно ввести все уравнения системы\

4. Записать Find(x)

5. Установить знак =

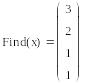
Если система содержит большое количество уравнений, удобнее применять матричную форму.

Алгоритм выполнения:

1.Ввести матрицу коэффициентов при неизвестных

2. Ввести вектор свободных членов

3. Ввести начальные значения корней через вектор

4. Ввести ключевое слово Given

5. Записать систему в матричной форму

6. Применить метод Find

7. В вычислительном блоке логическое равно.

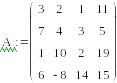
Самый простой способ решения почти всякой несингулярной системы является алгоритм исключения Гаусса.

Алгоритм исключения Гаусса

Алгоритм последовательных исключений Гаусса основан на преобразовании матрицы A линейной системы Ax=b к треугольному виду (т.е. к форме, когда все элементы ниже главной диагонали матрицы являются нулевыми). Точнее, СЛАУ Ax=b заменяется эквивалентной системой с другой матрицей A* и другим вектором правых частей b*, но имеющей то же решение, что и исходная система.

Алгоритм состоит в следующем:

1. Проводится прямой ход исключения неизвестных путем подстановки одних уравнений в другие. Используются следующие формулы: a_ij = - a_ij / a_jj a_ik = a_ik + a_ija_ik b_j = b_j + a_ijb_j j = 1,2, ... N-1     i=j+1,  j+2, ... N   k=j+1,  j+2, ... j+N  

2. При помощи обратного хода определяются все неизвестные х. Для этого х_N сразу определяется из последнего уравнения, в которое не входят другие х (матрица системы теперь является трехдиагональной). Затем х_N  подставляется в предыдущее  уравнение, из которого сразу определяется х_N-1 и т.д.

Этот метод реализован во встроенной функции lsolve.

При использовании этого метода система уравнений должна быть записана в матричной форме.

Алгоритм выполнения:

1. Ввести матрицу с коэффициентами при неизвестных

2. Ввести столбец свободных членов

3. Записать функция lsolve

4. При численном решении после функции ставится знак =, а

п ри символьном 

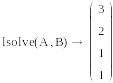
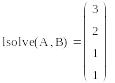
М ожно провести проверку:

Произвольные системы линейных уравнений

Классические задачи решения систем линейных уравнений предполагают равное количество уравнений и неизвестных . Рассмотрим теперь системы, в которых матрица коэффициентов при неизвестных является неквадратной либо плохо обусловлена.