Нелинейные алгебраические уравнения

Огромное количество задач вычислительной математики связано с решением нелинейных алгебраических уравнений.

Постановка задач выглядит следующим образом.

Пусть имеется алгебраическое уравнение с неизвестным х:

F(x)=0

Требуется найти корни, т.е. все значения х, которые переводят уравнение в верное равенство. Относительно небольшое количество задач отыскания корней алгебраических уравнений можно решить аналитически, а на практике почти всегда приходится искать решение при помощи численных методов.

Для решения систем нелинейных уравнений или одного уравнения применяется вычислительный блок Given/Find, состоящий из трёх частей.

• Given –ключевое слово.

• Система, записанная логическими операторами в виде равенств и, возможно, неравенств;

• Find ( 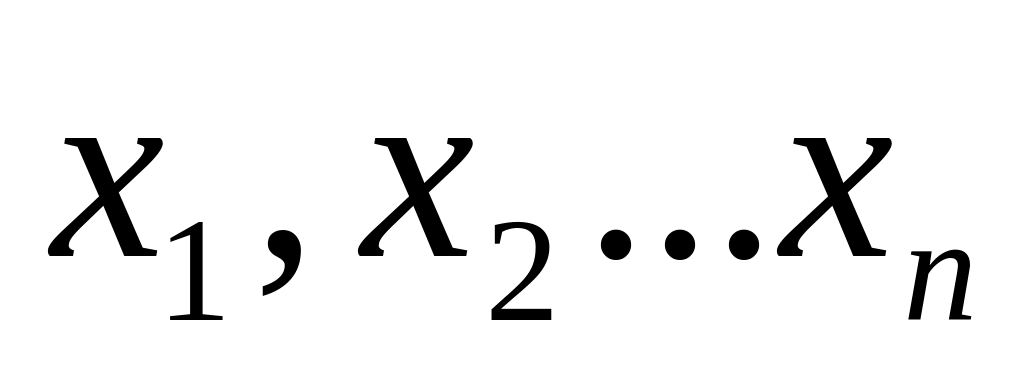) –встроенная функция для решения системы уравнений относительно переменных .

Логические операторы вставляются с помощью панели инструментов Boolean.

Пример:

Решить кубическое уравнение с одним неизвестным х.

На отрезке [-2;2] из графика видно, что уравнение имеет три корня.

Это аналитическое решение данного уравнения.

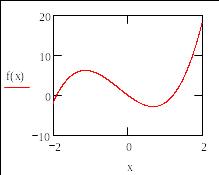
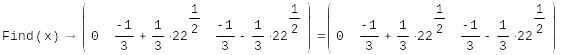
Пример: С 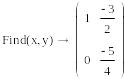имвольное решение системы двух уравнений

Численное решение уравнений

Отыскание корней алгебраического уравнения численными методами связано с двумя задачами:

• Локализация корней, т.е. определение их существования, количества, примерного расположения.

• Отыскание корней с заданной точностью, т.е. найти корни, при которых значение функции отличается от 0 не более, чем на TOL.

Для численного решения систем уравнений применяется тот же самый вычислительный блок, что и для символьных вычислений. При численных вычислениях может быть найден только один из корней уравнения.

Отличия численного нахождения корней от символьного:

1. Вместо оператора символьного вывода используется оператор численного вывода (=).

2. Перед вычислительным блоком должны быть заданы начальные значения для всех неизвестных.

П ример:

Р ешение кубического уравнения

Р ешение системы из двух уравнений

Системы линейных уравнений

Центральным вопросом вычислительной линейной алгебры является решение систем линейных алгебраических уравнений (СЛАУ), т. е. систем уравнений вида  a_i1 x₁+a_i2 x₂+...+a_iNx_N=b_i.                 (1) В матричной форме СЛАУ записывается в эквивалентном виде: Ax=b,                                                (2) где A - матрица коэффициентов СЛАУ размерности N², x - вектор неизвестных, b - вектор правых частей уравнений. К системам линейных уравнений сводится множество, если не сказать большинство, задач вычислительной математики.

СЛАУ имеет единственное решение, если матрица A является невырожденной, или по-другому, несингулярной, т. е. ее определитель не равен нулю. С вычислительной точки зрения, решение СЛАУ не представляет трудностей, если матрица A не очень велика. С большой матрицей проблем также не возникнет, если она не очень плохо обусловлена.