Векторы являются частным случаем, поэтому для них справедливы все те операции, что и для матриц. Но есть и специфические операторы.

Модуль вектора

Модуль вектора по определению равен квадратному корню из суммы

квадратов его элементов.

1. Установить оператор символьного вывода 

2. Слева поставить модуль, ввести вектор

3. Справа результат

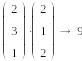
Скалярное произведение

Скалярное произведение определяется как скаляр, равный сумме попарных произведений соответствующих элементов. Векторы должны иметь одинаковую размерность, скалярное произведение имеет ту же размерность.

1. Установить знак символьного вывода

2. Установить знак умножения

3. Заполнить местозаполнители, используя матричную панель.

Векторное произведение

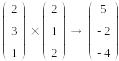Векторное произведение двух векторов u и v с углом σ между ними равно вектору с модулем |u|*|v|*sinσ, направленным перпендикулярно плоскости векторов u и v. Обозначают векторное произведение символом «х», который можно ввести нажатием кнопки Cross Product (векторное произведение) в панели Matrix (Матрица) или сочетанием клавиш <Ctrl>+<8>.

1. Установить оператор символьного вывода

2. Установить символ «х» из панели Matrix.

3. Заполнить местозаполнители.

Определитель квадратной матрицы

Определитель в Mathcad обозначается традиционно стандартным математическим символом. Чтобы ввести оператор нахождения определителя матрицы, можно нажать кнопку Determinat на панели инструментов Matrix или набрать на клавиатуре | |, нажав клавиши Ctrl + <\>.

1. П 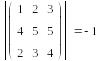оставить знак =

2. Установить | |.

3. Ввести матрицу.

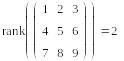
Ранг матрицы

Рангом матрицы называют наибольшее натуральное число k, для которого существует не равный нулю определитель k-порядка подматрицы, составленной из любого пересечения k столбцов и k строк матрицы.

Для вычисления ранга матрицы в Mathcad предназначена функция rank.

Обращение квадратной матрицы

Поиск обратной матрицы возможен, если матрица квадратная и её определитель не равен нулю. Произведение исходной матрицы на обратную по определению является единичной матрицей. Для ввода оператора поиска обратной матрицы нажать кнопку Inverse (Обратная матрица) на панели инструментов Matrix.

1. Установить знак =.

2. Слева нажать кнопку Inverse и ввести матрицу.

3. Справа появится обратная матрица.

Сортировка элементов матрицы

Элементы матрицы можно отсортировать по возрастанию или убыванию. Для этого имеются несколько встроенных функций, которые позволяют гибко управлять сортировкой матриц.

• sort(v)-сортировка элементов вектора в порядке возрастания.

• reverse(v)-перестановка элементов вектора в обратном порядке

• csort(A,i) –сортировка i -столбца по возрастанию

• rsort(A,i) –сортировка i - строки по возрастанию

Сортировка вектора

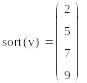
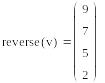
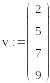
Сортировка матриц по строке и столбцу

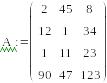
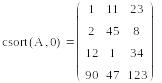
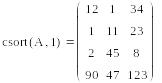
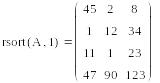
Вывод размера матрицы

Для получения сведений о характеристиках матриц или векторов предусмотрены следующие встроенные функции:

• rows(A)-число строк.

• cols(A) – число столбцов.

• length(v) – число элементов вектора.

• last(v) – индекс последнего элемента вектора.
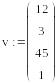