Двухточечные краевые задачи
Решение краевых задач для систем обыкновенных дифференциальных уравнений методом стрельбы в Mathcad достигается применением двух встроенных функций. Одна из них предназначена для двухточечных задач с краевыми условиями, заданными на концах интервала.
Sbval(z,x0,x1,D,load,score)-поиск вектора недостающих L начальных условий для двухточечной краевой задачи для системы N ОДУ:
Z-вектор размера Lx1, присваивающий недостающим начальным условиям (на левой границе интервала) начальные значения;
X0-левая граница расчётного интервала;
X1-правая граница расчётного интервала;
Load(x0,z)-векторная функция размера Nx1 левых граничных условий, причём недостающие начальные условия поименовываются соответствующими компонентами векторного аргумента;
Score(x1,y)-векторная функция размера Lx1, выражающая L правых граничных условий для векторной функции y в точке x1;
D(x,y)-векторная функция, описывающая систему N ОДУ, размера Nx1 и двух аргументов – скалярного х и векторного у. При этом у-это неизвестная векторная функция аргумента х того же размера Nx1.
П
ример:
Решение краевой задачи:
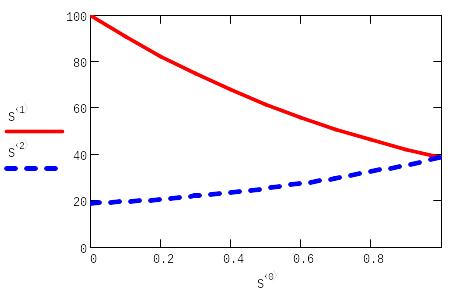
Реализованный в функции sbval алгоритм стрельбы ищет недостающие начальные условия таким образом, чтобы решение полученной задачи Коши делало функцию score(x,y) как можно ближе к нулю.
Краевые задачи с условием во внутренней точке
Рассмотрим реализацию алгоритма стрельбы с граничными условиями не только на концах интервала, но и с дополнительными условиями в некоторой промежуточной точке расчётного интервала. Для выполнения этой задачи существует функция:
Bvalfit(z1,z2,x0,x1,xf,D,load1,load2,score)-поиск вектора недостающих граничных условий для краевой задачи с дополнительным условием в промежуточной точке для системы ОДУ:
Z1-вектор, присваивающий недостающим начальным условиям на левой границе интервала начальные значения;
Z2- вектор того же размера, присваивающий недостающим начальным условиям на правой границе интервала начальные значения;
X0-левая граница расчётного интервала;
X1-правая граница расчётного интервала;
Xf-точка внутри интервала;
D(x,y)- векторная функция, описывающая систему N ОДУ, размера Nx1 и двух аргументов – скалярного х и векторного у. При этом у-это неизвестная векторная функция аргумента х того же размера Nx1.
Load1(x0,z)- векторная функция размера Nx1 левых граничных условий, причём недостающие начальные условия поименовываются соответствующими компонентами векторного аргумента z;
Load2(x1,z)- векторная функция размера Nx1 левых граничных условий, причём недостающие начальные условия поименовываются соответствующими компонентами векторного аргумента;
Score(xf,y)- векторная функция размера Lx1, выражающая внутреннее условие для векторной функции y в точке xf;
Примечание: обычно функция Bvalfit применяется для задач, в которых производная имеет разрыв во внутренней точке xf. Некоторые из этих задач не возможно решить обычными методами пристрелки, поэтому пристрелку приходится вести из двух граничных точек. Внутреннее условие в точке xf
я
вляется
просто условием сшивки в ней левого и
правого решений. Рассмотрим
работу этой функции на том же примере
модели взаимодействия пучков света,
предположив, что в промежутке xf=0.5
и x1=1
находится более плотная среда с
коэффициентом ослабления излучения
a(x)=3.
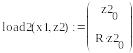
