Краевые задачи для оду

Рассмотрим краевые задачи для систем ОДУ, в которых часть граничных условий поставлена в начальной точке интервала, а остальная часть - в его конечной точке. Для решения краевых задач предусмотрены соответствующие численные методы, в частности алгоритм пристрелки. Краевые задачи во множестве практических приложений часто зависят от некоторого числового параметра. При этом решение существует не для всех его значений, а лишь для счетного их числа. Такие задачи называют уже задачами на собственные значения.

Постановка краевых задач для ОДУ отличается от задач Коши, рассмотренных ранее, тем, что граничные условия для них ставятся не в одной начальной точке, а на обеих границах расчетного интервала. Если имеется система N обыкновенных дифференциальных уравнений первого порядка, то часть из N условий может быть поставлена на одной границе интервала, а оставшиеся условия - на противоположной границе. Дифференциальные уравнения высших порядков можно свести к эквивалентной системе ОДУ первого порядка.

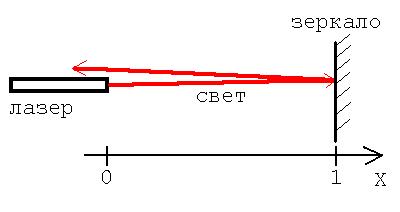
Рассмотрим постановку краевых задач на конкретном физическом примере модели взаимодействия встречных световых пучков.

Предположим, что надо определить распределение интенсивности оптического излучения в пространстве между источником (лазером) и зеркалом, заполненном некоторой средой.

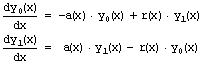Будем считать, что от зеркала отражается R-я часть падающего излучения (т. е., его коэффициент отражения равен R), а среда как поглощает излучение с коэффициентом ослабления a(x), так и рассеивает его. Причем коэффициент рассеяния назад равен r(x). В этом случае закон изменения интенсивности y0(x) излучения, распространяющегося вправо, и интенсивности y1(x) излучения влево определяется системой двух ОДУ первого порядка:

Для правильной постановки задачи требуется помимо уравнений задать такое же количество граничных условий. Одно из них будет выражать известную интенсивность излучения I0, падающего с левой границы x=0, а второе - закон отражения на его правой границе x=1:

Рис. 1. Модель для постановки краевой задачи

Полученную задачу называют краевой (boundary value problem ), так как условия поставлены не на одной, а на обеих границах интервала (0,1). И, в связи с этим, их не решить методами предыдущей главы, предназначенными для задач с начальными условиями. Далее для показа возможностей Mathcad будем использовать этот пример с R= 1и конкретным видом

a(x)=const= 1и r(x)=const=0.1, описывающим случай изотропного (не зависящего от координаты x) рассеяния.

Алгоритм стрельбы

Для решения краевых задач в Mathcad реализован наиболее популярный алгоритм, называемый методом стрельбы или пристрелки (shooting method). Он сводит решение краевой задачи к решению серии задач Коши с различными начальными условиями. Суть метода стрельбы заключается в пробном задании недостающих граничных условий на левой границе интервала и решении затем полученной задачи Коши хорошо известными методами. В нашем примере не хватает начального условия для y1(0), поэтому сначала зададим ему произвольное значение, например y1(0)=10. Конечно, такой выбор не совсем случаен, поскольку из физических соображений ясно, что, во-первых, интенсивность излучения - величина заведомо положительная, и, во-вторых, отраженное излучение должно быть намного меньше падающего.

 Пример: Решение пробной задачи Коши для модели распространения света

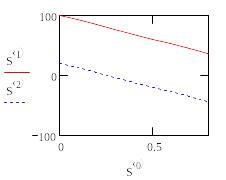
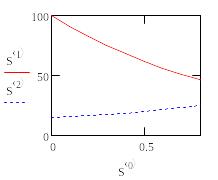
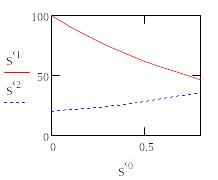
Из графика видно, что взятое наугад второе начальное условие не обеспечило выполнение граничного условия при x= 1. И понятно, что для лучшего выполнения этого граничного условия следует взять большее значение y1(0). Возьмем, например, y1(0)= 15, и вновь решим задачу Коши, далее y1(0)= 20, y1(0)= 25. Продолжая подобным образом "пристрелку" по недостающему начальному условию, возможно отыскать правильное решение краевой задачи.

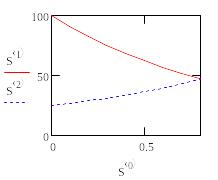
Рис.Иллюстрация метода стрельбы

В этом и есть принцип алгоритма стрельбы. Выбирая пробные начальные условия (проводя пристрелку) и решая соответствующую серию задач Коши, можно  найти то решение системы ОДУ, которое (с заданной точностью) удовлетворит граничному условию (или, в общем случае, условиям) на другой границе расчетного интервала.