- •Основы вычислений
- •Типы данных
- •Cтроковые переменные
- •Работа с массивами
- •Принцип программирования в Mathcad
- •Логические операторы
- •Матричные операторы
- •Операторы выражения
- •Функции
- •Элементарные функции
- •Функция вывода текущего времени
- •Вычисление рядов и произведений
- •Вычисление предела
- •Простейшие матричные операции Транспонирование
- •Сложение и вычитание матриц
- •Векторы являются частным случаем, поэтому для них справедливы все те операции, что и для матриц. Но есть и специфические операторы.
- •Определитель квадратной матрицы
- •Ранг матрицы
- •Обращение квадратной матрицы
- •Сортировка элементов матрицы
- •Вывод размера матрицы
- •Нелинейные алгебраические уравнения
- •Численное решение уравнений
- •Системы линейных уравнений
- •Решение слау с использованием вычислительного блока Given/Find
- •Алгоритм исключения Гаусса
- •Произвольные системы линейных уравнений
- •Переопределённые системы
- •Недоопределённые системы
- •Вырожденные системы линейных уравнений
- •Регуляризация
- •Матричные разложения
- •Разложение Холецкого
- •Обыкновенные дифференциальные уравнения
- •Задачи Коши для оду
- •Дифференциальные уравнения n-го порядка
- •Схемы Рунге-Кутта
- •Система n дифференциальных уравнений
- •Решение систем оду в одной заданной точке
- •Жёсткие системы оду
- •Примеры динамических моделей
- •Модель "хищник-жертва"
- •Модель генератора автоколебаний
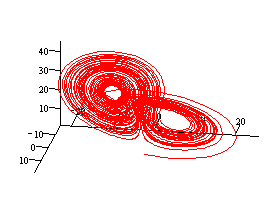
- •Модель Лоренца
- •Краевые задачи для оду
- •Алгоритм стрельбы
- •Двухточечные краевые задачи
- •Краевые задачи с условием во внутренней точке
Примеры динамических моделей
Динамическими системами принято называть класс задач, представленных задачами Коши для дифференциальных уравнений (обыкновенных - иначе ОДУ, или в частных производных) или систем таких уравнений.
Наиболее просты примеры исключительно линейных уравнений, т. е. содержащих только первую степень неизвестных функций и их производных, как, к примеру модель линейного гармонического осциллятора. Линейные дифференциальные уравнения легко решаются аналитически, а необходимость применения численных методов возникает, когда число таких уравнений в системе ОДУ очень велико. Линейные ОДУ хорошо изучены, и в них могут существовать лишь простые типы аттракторов (центр, фокус, седло).
Тип аттрактора характеризуется свойствами конкретных динамических систем. Различают следующие типы аттракторов - особых точек в фазовом пространстве
Узел: Центр:

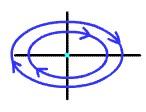
Фокус: Седло:
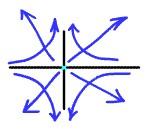
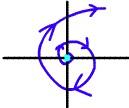
Аттракторы могут быть либо устойчивыми (тогда траектории в фазовом пространстве стремятся к ним), так и неустойчивыми (тогда траектории, даже начинающиеся очень близко от особой точки, отталкиваются от нее - такие особые точки называют репеллерами).
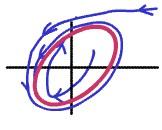
 Помимо
особых точек существуют аттракторы -
предельные циклы, а также очень необычные
странные аттракторы:
Предельный
цикл: Странный
аттрактор:
Помимо
особых точек существуют аттракторы -
предельные циклы, а также очень необычные
странные аттракторы:
Предельный
цикл: Странный
аттрактор:
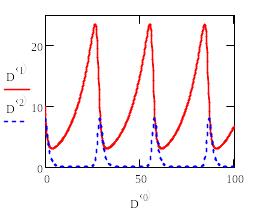
Между тем, многие нелинейные уравнения демонстрируют совершенно удивительные свойства, причем решение подавляющего большинства из них можно получить лишь численно. Рассмотрим несколько наиболее известных классических примеров систем ОДУ.
Это модели нелинейного осциллятора, динамики популяций (Вольтерра), электронного генератора автоколебаний (Ван дер Поля), турбулентной конвекции жидкости (Лоренца) и химической реакции с диффузией (Пригожина).
Все примеры являются типичными динамическими системами и содержат производные по времени t, описывая динамику различных физических параметров. Приведем примеры и графики решений и фазовые портреты для некоторых моделей.
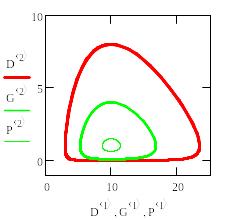
Модель "хищник-жертва"
Модель
взаимодействия "хищник-жертва"
независимо предложили в 1925-1927 гг. Лотка
и Вольтерра. Два дифференциальных
уравнения моделируют временную динамику
численности двух биологических популяций
жертвы y0
и хищника y1.
Предполагается, что жертвы размножаются
с постоянной скоростью C, а их численность
убывает вследствие поедания хищниками.
Хищники же размножаются со скоростью,
пропорциональной количеству пищи (с
коэффициентом r) и умирают естественным
образом (смертность определяется
константой D).
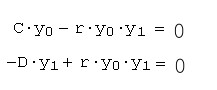 Модель замечательна тем, что в
такой системе наблюдаются циклическое
увеличение и уменьшение численности и
хищника и жертвы, так часто наблюдаемое
в природе. Фазовый портрет системы
представляет собой концентрические
замкнутые кривые, окружающие одну
стационарную точку, называемую центром.
Как видно, модельные колебания численности
обеих популяций существенно зависят
от начальных условий - после каждого
периода колебаний система возвращается
в ту же точку. Динамические системы с
таким поведением называют негрубыми.
Модель замечательна тем, что в
такой системе наблюдаются циклическое
увеличение и уменьшение численности и
хищника и жертвы, так часто наблюдаемое
в природе. Фазовый портрет системы
представляет собой концентрические
замкнутые кривые, окружающие одну
стационарную точку, называемую центром.
Как видно, модельные колебания численности
обеих популяций существенно зависят
от начальных условий - после каждого
периода колебаний система возвращается
в ту же точку. Динамические системы с
таким поведением называют негрубыми.
![]()
![]()
![]()
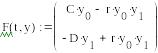
![]()
![]()
![]()
![]()
![]()
![]()