Решение систем оду в одной заданной точке

Достаточно часто при решении дифференциальных уравнений требуется определить значения искомых функций не на всём интервале (t0,t1), а только в последней его точке. Весьма распространены задачи поиска аттракторов динамических систем. Известно, что одна и та же система при разных начальных условиях при t∞ приходит в одну и ту же точку (аттрактор). Поэтому нужно определить эту точку.

Для решения этой задачи в Mathcad имеются модификации встроенных функций Rkadapt и Bulstoer. Они имеют другой набор параметров и работают быстрее своих аналогов.

• Rkadapt(y0,t0,t1,acc,D,k,s)-метод Рунге-Кутта с переменным шагом;

• Bulstoer(y0,t0,t1,acc,D,k,s)-метод Булирша-Штера:

  • y0-вектор начальных значений в точке t0;

  • t0,t1-начальная и конечная точки расчёта;

  • acc-погрешность вычисления;

  • D-векторная функция, задающая систему ОДУ;

  • K-максимальное число шагов, на которых численный метод будет находить решение;

  • S-минимально допустимая величина шага.

Пример:

Поиск аттрактора системы двух ОДУ модели осциллятора.

В первых двух строках определяется система уравнений и начальные условия; в следующей строке матрице u присваивается решение, полученное с помощью bulstoer.

В четвёртой строке определяем количество шагов, далее осуществлен вывод решения системы .

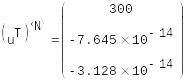
Жёсткие системы оду

Жесткие системы - это те уравнения, решение которых получить намного проще с помощью определенных неявных методов, чем с помощью явных методов.

Раccмотрим пример нежёсткого уравнения, решение которого получаем методом Рунге-Кутта.

Изменим коэффициент на -50:

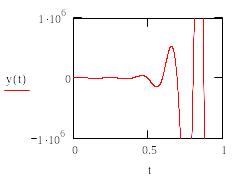
Разброс решения говорит о неустойчивости алгоритма. Первое, что можно сделать, - увеличить количество шагов в методе Рунге-Кутта.

М ожно убедиться, что при step>20 разболтка пропадает, и решение становится похожим на график с коэффициентом -10.

Таким образом, во-первых, мы выяснили, что одни и те же уравнения (с разными параметрами) могут быть как жесткими, так и нежесткими.

Во-вторых, чем жестче уравнение, тем больше шагов в обычных численных методах требуется для его устойчивого решения.

Решение жёстких систем дифференциальных уравнений можно осуществить только с помощью встроенных функций:

• Radau(y0,t0,t1,M,F)-алгоритм RADAUS для жёстких систем;

• Stiffb(y0,t0,t1,M,F,J) –алгоритм Булирша-Штера для жёстких систем ОДУ;

• Stiffr(y0,t0,t1,M,F,J) –алгоритм Розенброка для жёстких систем ОДУ;

  • Y0-вектор начальных значений в точке t0;

  • t0,t1-начальная и конечная точка расчёта;

  • M-число шагов численного метода;

  • F-векторная функция F(t,y) размера 1xN, задающая систему ОДУ.

  • J-матричная функция J(t,y) размера (N+1)xN , составленная из вектора производных функции F(t,y) по t.

Пример:

Рассмотрим предыдущую функцию, только с коэффициентом -100.

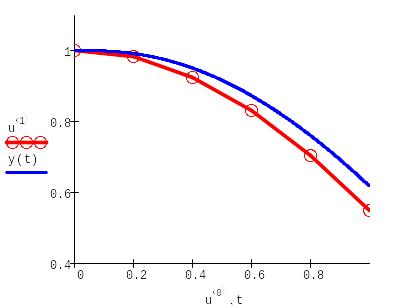
Существуют встроенные функции, которые применяются для решения жёстких систем ОДУ не на всём интервале, а только в заданной точке t1.

• Radau(y0,t0,t1,acc,F,k,s)-алгоритм RADAUS;

• Stiffb(y0,t0,t1,acc,F,J,k,s) –алгоритм Булирша-Штера ;

• Stiffr(y0,t0,t1,acc,F,J,k,s) –алгоритм Розенброка ;