
- •Основы вычислений
- •Типы данных
- •Cтроковые переменные
- •Работа с массивами
- •Принцип программирования в Mathcad
- •Логические операторы
- •Матричные операторы
- •Операторы выражения
- •Функции
- •Элементарные функции
- •Функция вывода текущего времени
- •Вычисление рядов и произведений
- •Вычисление предела
- •Простейшие матричные операции Транспонирование
- •Сложение и вычитание матриц
- •Векторы являются частным случаем, поэтому для них справедливы все те операции, что и для матриц. Но есть и специфические операторы.
- •Определитель квадратной матрицы
- •Ранг матрицы
- •Обращение квадратной матрицы
- •Сортировка элементов матрицы
- •Вывод размера матрицы
- •Нелинейные алгебраические уравнения
- •Численное решение уравнений
- •Системы линейных уравнений
- •Решение слау с использованием вычислительного блока Given/Find
- •Алгоритм исключения Гаусса
- •Произвольные системы линейных уравнений
- •Переопределённые системы
- •Недоопределённые системы
- •Вырожденные системы линейных уравнений
- •Регуляризация
- •Матричные разложения
- •Разложение Холецкого
- •Обыкновенные дифференциальные уравнения
- •Задачи Коши для оду
- •Дифференциальные уравнения n-го порядка
- •Схемы Рунге-Кутта
- •Система n дифференциальных уравнений
- •Решение систем оду в одной заданной точке
- •Жёсткие системы оду
- •Примеры динамических моделей
- •Модель "хищник-жертва"
- •Модель генератора автоколебаний
- •Модель Лоренца
- •Краевые задачи для оду
- •Алгоритм стрельбы
- •Двухточечные краевые задачи
- •Краевые задачи с условием во внутренней точке
Схемы Рунге-Кутта
Семейство схем Рунге-Кутта основано на аппроксимации неизвестных аргументов y(tn) в правых частях дифференциальных уравнений f(t,y).
Р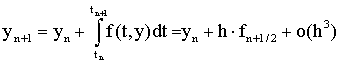 ассмотрим
идею этих методов на примере алгоритма
2-го порядка.
Выпишем точную формулу
интегрирования ОДУ на n-м шаге численного
решения:
ассмотрим
идею этих методов на примере алгоритма
2-го порядка.
Выпишем точную формулу
интегрирования ОДУ на n-м шаге численного
решения:
![]() В
формуле
В
формуле
![]() не
знаем, чему равно yn+1/2.
Возьмем его из формулы явного алгоритма
Эйлера:
не
знаем, чему равно yn+1/2.
Возьмем его из формулы явного алгоритма
Эйлера:
и подставим в основную формулу интегрирования шага ОДУ. В результате получим следующий алгоритм реализации шага:
![]()
![]() где
где
В![]()
![]() зависимости от выбора метода интегрирования
ОДУ на элементарном шаге и конкретной
формы аппроксимации y (t) в правой
части ОДУ, получаются алгоритмы различной
точности и быстродействия. Наиболее
популярен алгоритм Рунге-Кутта четвертого
порядка, описанный в большинстве книг
по методам вычислений. Он обеспечивает
малую погрешность для широкого класса
систем ОДУ за исключением жестких систем
и, при этом, довольно экономичен (на
каждом шаге интегрирования требуется
вычисление 4-х значений функции f):
зависимости от выбора метода интегрирования
ОДУ на элементарном шаге и конкретной
формы аппроксимации y (t) в правой
части ОДУ, получаются алгоритмы различной
точности и быстродействия. Наиболее
популярен алгоритм Рунге-Кутта четвертого
порядка, описанный в большинстве книг
по методам вычислений. Он обеспечивает
малую погрешность для широкого класса
систем ОДУ за исключением жестких систем
и, при этом, довольно экономичен (на
каждом шаге интегрирования требуется
вычисление 4-х значений функции f):
![]()
![]()
Если по различным причинам время расчетов становится критичным или точность неудовлетворительной, стоит попробовать вместо рассмотренного алгоритма Рунге-Кутта с фиксированным шагом другие методы.
Например, если известно, что решение на рассматриваемом интервале меняется слабо, либо существуют участки медленных и быстрых его изменений, Метод Рунге-Кутта с переменным шагом основан на разбиении интервала не на равномерные шаги, а более оптимальным способом.
Там, где решение меняется слабо, шаги выбираются более редкими, а в областях его сильных изменений - частыми. Это очень просто осуществить, т.к. алгоритм Рунге-Кутта является одношаговым и подразумевает простой пересчет при любом значении шага hn искомого y (tn+hn) через y (tn).
Таким образом, легко обобщить алгоритм на адаптированный вариант, с выбором на каждом шаге своего hn в зависимости от локальной динамики решения на предыдущих шагах.
В результате применения адаптированного алгоритма, для достижения одинаковой точности может потребоваться существенно меньшее число шагов, чем для стандартного алгоритма Рунге-Кутта с фиксированным шагом.
Система n дифференциальных уравнений
При помощи Mathcad можно решать системы N>=1 ОДУ первого порядка, если они записаны в стандартной форме Коши y'(t)=f(y(t),t).
В Mathcad имеется несколько встроенных функций, которые позволяют решать задачу Коши различными численными методами. Для нежёстких систем ОДУ применяются следующие функции:
rkfixed(y0,t0,t1,M,D) –метод Рунге-Кутты с фиксированным шагом;
Rkadapt(y0,t0,t1,M,D)- метод Рунге-Кутты с переменным шагом;
Bulstoer(y0,t0,t1,M,D)- метод Булирша-Штера;
y0 –вектор начальных знаний в точке t0 размера Nx1 ;
t0 –начальная точка расчёта;
t1-конечная точка расчёта;
M- число шагов, на которых численный метод находит решение;
D –векторная функция размера Nx1 двух аргументов –скалярного t и векторного y. При этом y- искомая векторная функция аргумента t того же размера Nx1.
Примечание:
Регистр первой буквы в методе актуален.
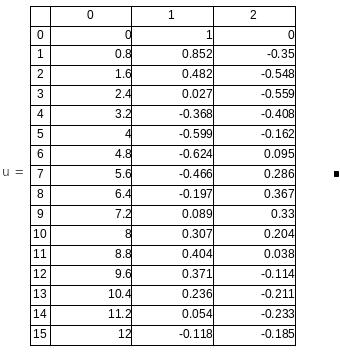
Каждая из приведённых функций выдаёт решение в виде матрицы размера (M+1)x(N+1). В её левом столбце находятся значение аргумента t, делящие интервал на равномерные шаги, а в остальных N – столбцах – значения искомых функций .
Пример:
Решим систему ОДУ осциллятора с затуханием с помощью функции
rkfixed.
![]()
![]()
![]()
![]()
Примечание:
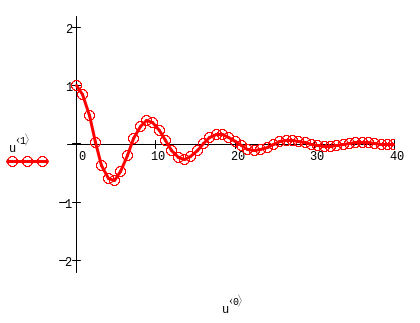
Скобки в графике устанавливаются с помощью комбинации клавиш <Ctrl>+<6>.
Результат расчёта представлен в виде матрицы и в виде графика.
Чтобы использовать другой численный алгоритм, достаточно поменять имя функции в последней строке на другую.
Пример:
![]() Решение
задачи Коши для обыкновенного
дифференциального уравнения первого
порядка
Решение
задачи Коши для обыкновенного
дифференциального уравнения первого
порядка
![]()
![]()
![]()
