Задачи Коши для оду
ОДУ первого порядка может по определению содержать помимо самой искомой функции y(t) только ее первую производную y'(t).
В подавляющем большинстве случаев дифференциальное уравнение можно записать в стандартной форме (форме Коши): y'(t)=f(y(t),t).
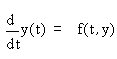
Задача Коши для системы - решить ОДУ с начальным условием
y(0)= C.
Искомая функция y(t) может быть вектором, т.е. включать несколько (L) неизвестных функций y1(t), ... , yL(t).
Тогда, соответственно, должно быть поставлено L начальных условий.
Стандартные процедуры Mathcad применимы для систем ОДУ первого порядка. Но если в систему входят и уравнения высших порядков, то её можно свести к системе большего числа уравнений первого порядка.
Пример:
Рассмотрим уравнение второго порядка модели осциллятора.
Модель
гармонического осциллятора описывает,
в частности, колебания маятника: y(t)
описывает изменения угла его отклонения
от вертикали; y'(t)-угловую скорость
маятника;
-ускорение,
а начальные условия, соответственно,
начальное отклонение маятника y(0)=1.0
и начальную скорость y'(0)=0. Модель
является линейной.(модель затухающего
гармонического осциллятора).
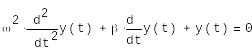
Примечание:
Символ производной набирается с помощью сочетания клавиш
<Ctrl>+<F7>.
Модели, основанные на задачах Коши для ОДУ, часто называют динамическими системами. Они содержат производную по времени t и описывают динамику некоторых параметров.
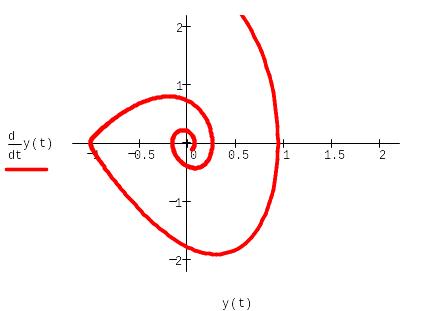
Для изучения динамических систем центральным моментом является анализ фазовых портретов, т.е. решений, получающихся при выборе всевозможных начальных условий.
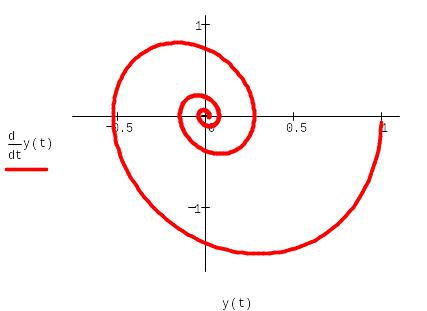Решение
ОДУ удобнее изображать в фазовом
пространстве, по каждой из осей которого
откладываются значения каждой из
найденных функций. При таком построении
графика аргумент t
будет присутствовать на нём лишь
параметрически. Фазовое пространство
является координатная плоскость, а
решение представляет собой кривую, или
по-другому, траекторию, выходящую из
точки, координаты которой равны начальным
условиям.
Дифференциальные уравнения n-го порядка
Для решения ОДУ порядка N>=1 в Mathcad предусмотрены две возможности:
Вычислительный блок Given/Odesolve - в этом случае решение имеет вид функции от t;
Встроенные функции решения систем ОДУ, причём уравнениявысших порядков необходимо свести к эквивалентной системе уравнений первого порядка. В этом случае решение имеет формат вектора.
Вычислительный блок для решения ОДУ, реализующий численный метод Рунга-Кутты, состоит из трёх частей:
Given-ключевое слово;
ОДУ и начальные условия в формате y(t0)=b записанные с помощью логических операторов, которые должны набираться на панели инструментов Boolean;
Odesolve(t,t1)-встроенная функция для решения ОДУ относительно переменной t на интервале (t0,t1), причём t0<t1.
Пример:
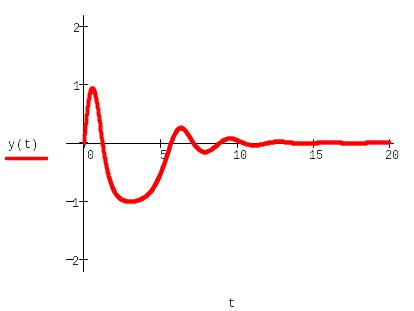
Решение задач Коши для ОДУ второго порядка (модель нелинейного осциллятора).
В примере можно применить различные модификации метода Рунга-Кутта. Для смены метода необходимо нажатием правой кнопки мыши на области функции Odesolve вызвать контекстное меню и выбрать в нём один из трёх пунктов: Fixed - (с фиксированным шагом); Adaptive- (Адаптивный); Stiff- (Для жёстких ОДУ).