Матричные разложения
При решении систем линейных уравнений с треугольной матрицей
видно, что за минимальное число операций получен ответ.
Поэтому удобно свести задачи решения систем общего вида к системам с треугольной матрицей.
Пример:
Решить систему с треугольной матрицей. (прямой ход)
Создадим пользовательскую функцию trg, используя элементы программирования.
Найдём корни и проведём проверку.
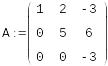
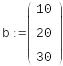
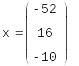
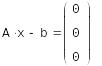
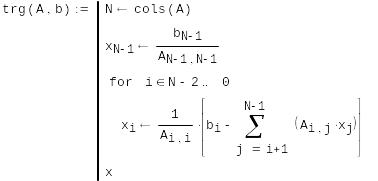
Разложение Холецкого
Разложением Холецкого симметричной матрицы А является представление вида
где L- треугольная матрица.
Алгоритм Холецкого реализован во встроенной функции cholesky.
Пример:
Разложение Холецкого:
Ввести матрицу А
Записать разложение Холецкого
Получить матрицу L
Получить
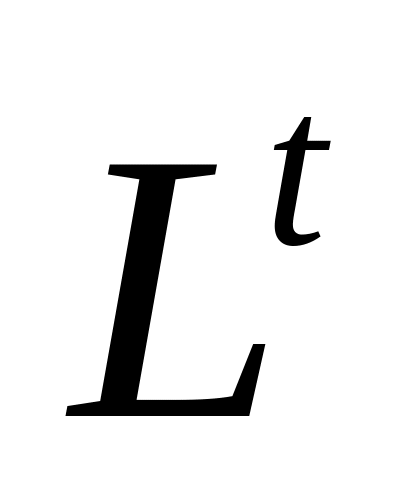
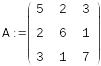
Решение системы, если известно разложение, основано на замене исходной системы A*x=b другой системой L*y=b (где y= *x).
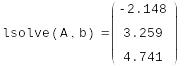
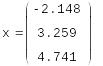
LU - разложение
Прямой ход алгоритма Гаусса можно записать в матричной форме: A=LU, где L и U - нижняя и верхняя треугольные матрицы соответственно. А,L,U - квадратные матрицы одного порядка. Элементы матриц L и U получаются явно в ходе работы прямого хода алгоритма Гаусса.
Такое представление матрицы А называют LU-разложением, или треугольным разложением.
Lu(A)-LU-разложение матрицы.
Результатом работы встроенной функции LU-разложения является матрица, составленная из матриц L и U соответственно. Чтобы выделить сами матрицы LU-разложения, а именно P,L,U необходимо применить функцию выделения подматрицы submatrix.
Пример:
Получим LU-разложение матрицы:
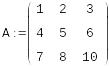
Пример:
Решение системы при помощи LU- разложения:
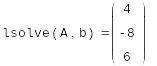
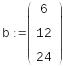
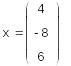
Обыкновенные дифференциальные уравнения
Дифференциальные уравнения являются разновидностью математических моделей, описывающих природные и технологические процессы.
Дифференциальные уравнения - это уравнения, в которых неизвестными являются не переменные (т. е. числа), а функции одной или нескольких переменных. Эти уравнения (или системы) включают соотношения между искомыми функциями и их производными. Если в уравнения входят производные только по одной переменной, то они называются обыкновенными дифференциальными уравнениями ( сокращение ОДУ). В противном случае говорят об уравнениях в производных.
Таким образом, решить (иногда употребляют другое слово проинтегрировать) дифференциальное уравнение -значит определить неизвестную функцию на определенном интервале изменения ее переменных.
Как известно, одно обыкновенное дифференциальное уравнение или система ОДУ имеет единственное решение, если помимо уравнения определенным образом заданы начальные или граничные условия.
Имеются два типа задач: 1. Задачи Коши - для которых определены начальные условия на искомые функции, т. е. заданы значения этих функций в начальной точке интервала интегрирования уравнения; 2. Краевые задачи - для которых заданы определенные соотношения сразу на обеих границах интервала.
Как правило, решение задач Коши для ОДУ и их систем - задача, хорошо разработанная и с вычислительной точки зрения не слишком сложная. Большое значение здесь имеет представление результатов и анализ зависимостей решения от различных параметров системы.
Между тем, имеется целый класс ОДУ, называемых жесткими, который не поддается решению стандартными методами, типа методов Рунге-Кутта. Для них имеются специальные алгоритмы.