
Указания к выполнению контрольной работы №1
Задание 1
Решить систему линейных алгебраических уравнений по правилу Крамера:
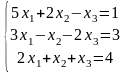
Решение:
Рассмотрим определитель системы
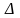 ,
составленный из коэффициентов, стоящих
при неизвестных:
,
составленный из коэффициентов, стоящих
при неизвестных:
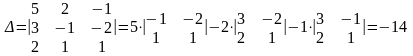 .
.
Определитель системы
 ,
следовательно, система определенная
(имеет единственное решение), которое
можно найти по формулам Крамера:
,
следовательно, система определенная
(имеет единственное решение), которое
можно найти по формулам Крамера:
 ,
,
где
 - определители, полученные заменой в
определителе
- определители, полученные заменой в
определителе
 последовательно первого, второго и
третьего столбцов столбцом свободных
членов, а именно:
последовательно первого, второго и
третьего столбцов столбцом свободных
членов, а именно:
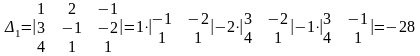
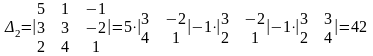

По формулам Крамера находим неизвестные:
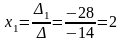 ,
,
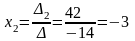 ,
,
Ответ:
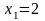 ,
,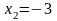 ,
,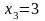 .
.
Задание 2
Решить систему линейных алгебраических уравнений матричным способом:
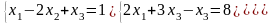
Решение:
Обозначим
через А
– матрицу коэффициентов при неизвестных;
Х
– матрицу-столбец неизвестных
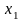 ,
,
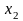 ,
,
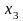 .,
В
– матрицу-столбец свободных членов:
.,
В
– матрицу-столбец свободных членов:
А=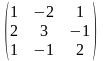 ,
Х=
,
Х=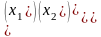 ,
В=
,
В=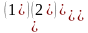 ,
,

С учетом этих обозначений данная система уравнений принимает следующую матричную форму:
А·Х=В (1)
Если матрица А – невырожденная квадратная матрица (ее определитель ∆ отличен от нуля), то она имеет обратную матрицу А-1. Умножив обе части равенства (1) слева на матрицу А-1, получим:
А-1·А·Х=А-1·В.
Но А-1·А=Е (Е – единичная матрица), а ЕХ = Х, поэтому,
Х=А-1·В. (2)
Равенство (2) называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо вычислить обратную матрицу А-1.
Пусть имеем невырожденную матрицу:
А=
 .
.
Тогда
А-1=
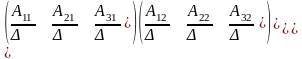 ,
,
где
Аij
(i=1,
2, 3; j=1,
2, 3) – алгебраическое дополнение элемента
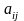 в определителе матрицы А,
которое является произведением
в определителе матрицы А,
которое является произведением
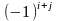 на минор (определитель) второго порядка,
полученный вычеркиванием i-й
строки и j-го
столбца в определителе матрицы А.
на минор (определитель) второго порядка,
полученный вычеркиванием i-й
строки и j-го
столбца в определителе матрицы А.
Вычислим определитель ∆ и алгебраические дополнения Аij элементов определителя матрицы А.
∆=
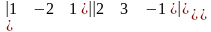 =6+2-2-(3+1-8)=6-(-4)=10
=6+2-2-(3+1-8)=6-(-4)=10
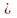 0
– следовательно, матрица А
невырожденная и имеет обратную матрицу
А-1.
0
– следовательно, матрица А
невырожденная и имеет обратную матрицу
А-1.
А11
=(−1)1+1.
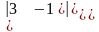 A12
=(−1)1+2.
A12
=(−1)1+2.
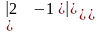
A13
=(−1)1+3.
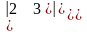 A21
=(−1)2+1.
A21
=(−1)2+1.

A22
=(−1)2+2.
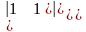 A23
=(−1)2+3.
A23
=(−1)2+3.
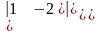
A31
=(−1)3+1.
A32
=(−1)3+2.
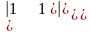
A33 =(−1)3+3.
Тогда
А-1
=
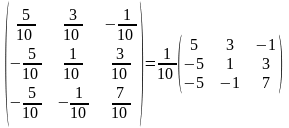 .
.
По формуле (2) находим решение данной системы уравнений в матричной форме:
Х=А-1·В= ·
·
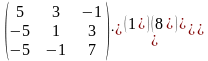
=
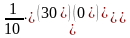
Отсюда
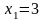 ,
,
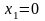 ,
,
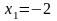 .
.
Задание 3
Решить систему линейных алгебраических уравнений методом Гаусса:
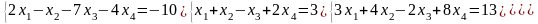 .
.
Решение:
Основной
матрицей
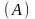 системы называется матрица, составленная
из коэффициентов, стоящих при неизвестных.
Запишем расширенную матрицу
системы называется матрица, составленная
из коэффициентов, стоящих при неизвестных.
Запишем расширенную матрицу
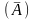 системы, состоящую из основной матрицы
системы, дополненной столбцом свободных
членов:
системы, состоящую из основной матрицы
системы, дополненной столбцом свободных
членов:
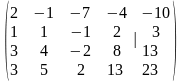
Используя элементарные преобразования матриц, приведем расширенную матрицу системы к ступенчатому виду.
Для облегчения вычислений, желательно, чтобы элемент, стоящий в первой строке и первом столбце, был равен единице. Поэтому, поменяем местами вторую и первую строки матрицы.
Для обнуления элементов первого столбца, расположенных ниже единицы, вычтем из второй строки первую, умноженную на два, из третьей строки вычтем первую, умноженную на три, и, наконец, из четвертой вычтем первую, умноженную также на три.
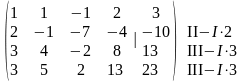
Получим матрицу:
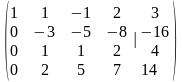
Аналогично, для облегчения вычислений, удобно чтобы второй элемент во второй строке был равен единице. Для этого поменяем местами вторую и третью строки.
Обнулим элементы второго столбца, стоящие ниже первого ненулевого элемента второй строки (единицы). Для этого к третьей строке прибавим вторую строку, умноженную на три, а из четвертой строки вычтем вторую, умноженную на два.
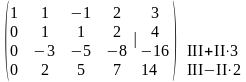
Получим матрицу:
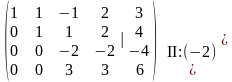
Опять же, желательно, чтобы третий элемент, стоящий в третьей строке, был равен единице. Для этого разделим третью строку на минус два, и, далее, из четвертой строки вычтем полученную третью, умноженную на три:
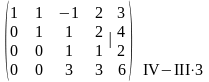
В итоге получим ступенчатую матрицу:
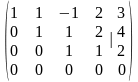 .
.
Ранг матрицы системы равен трем (числу ненулевых строк), ранг расширенной матрицы также равен трем. Следовательно, система совместная. Итак, ранг матрицы совместной системы равен трем, а число неизвестных равно четырем, следовательно, система неопределенная (имеет бесконечное множество решений).
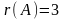 ,
,

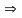 СЛУ совместная,
СЛУ совместная,
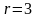 ,
,
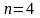 СЛУ неопределенная.
СЛУ неопределенная.
Ступенчатая матрица соответствует системе линейных уравнений:
 ,
,
Выразим
неизвестные
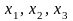 через
через
 ,
начиная с последнего уравнения:
,
начиная с последнего уравнения:
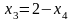 .
.
Подставим во второе уравнение вместо полученное выражение:
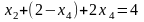 ,
,
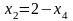 .
.
Аналогично,
вместо
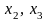 в первое уравнение подставим соответствующие
выражения:
в первое уравнение подставим соответствующие
выражения:
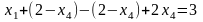 ,
,
 .
.
Получили следующую систему:
 .
.
Эта система линейных уравнений называется общим решением неопределенной системы. Подставляя вместо различные числовые значения, будем получать соответствующие частные решения.
Задание 4
Даны координаты вершин треугольника KLM: K (−4;-8), L(20;10), M(16;-18). Построить треугольник на координатной плоскости и найти: 1) длину стороны KL; 2) уравнение стороны KL и ее угловой коэффициент; 3)внутренний угол L; 4) уравнение высоты MN и ее длину; 5) уравнение медианы KS; 6) точку пересечения высоты MN и медианы KS; 7) площадь треугольника KLM; 8) уравнение окружности, для которой высота MN есть диаметр; 9) систему линейных неравенств, определяющих треугольник KLM.
Решение:
1)
Расстояние
d
между точками
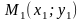 и
и
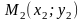 определяется по формуле:
определяется по формуле:
d
=
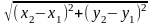 (1)
(1)
Подставив в эту формулу координаты точек K и L, имеем:
KL
=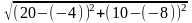 =
=
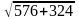 =30
=30
2) Уравнение прямой, проходящей через точки и , имеет вид:
 =
=
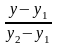 (2)
(2)
Подставив в (2) координаты точек K и L, получим уравнение прямой KL:
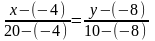 ,
,
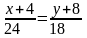 ,
,
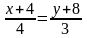 ,
,
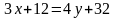 ,
,
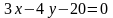 (KL).
(KL).
Для
вычисления углового коэффициента
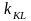 прямой KL
разрешим полученное уравнение относительно
у:
прямой KL
разрешим полученное уравнение относительно
у:
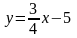 .
Отсюда
.
Отсюда
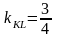 .
.
3)
Острый угол
 между двумя прямыми, угловые коэффициенты
которых равны
между двумя прямыми, угловые коэффициенты
которых равны
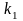 и
и
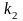 ,
определяется по формуле:
,
определяется по формуле:
tg
=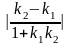 .
(3)
.
(3)
Из
чертежа видно, что угол KLM
в треугольнике, образованный прямыми
KL
и LM,
– острый. Тогда этот угол можно найти
по формуле (3), подставив в нее соответствующие
угловые коэффициенты. Угловой коэффициент
прямой LM
можно найти по формуле
 .
Тогда тангенс угла KLM
будет равен:
.
Тогда тангенс угла KLM
будет равен:
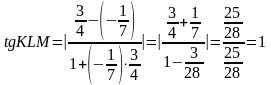 ,
,
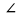 KLM
=
KLM
=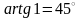
4) Так как высота MN перпендикулярна стороне KL, то из условия перпендикулярности прямых, угловые коэффициенты этих прямых обратны по величине и противоположны по знаку, т.е.
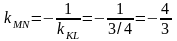 .
.
Уравнение прямой, проходящей через данную точку в заданном угловым коэффициентом k направлении, имеет вид:
 (4)
(4)
Подставив
в (4) координаты точки M
и найденный угловой коэффициент прямой
MN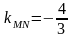 ,
получим уравнение высоты MN:
,
получим уравнение высоты MN:
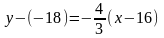 ,
,

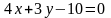 .
.
Для
нахождения длины MN
используем формулу расстояния от точки
до прямой
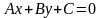 ,
т.к. расстояние от точки до прямой и есть
длина перпендикуляра, опущенного из
этой точки на прямую:
,
т.к. расстояние от точки до прямой и есть
длина перпендикуляра, опущенного из
этой точки на прямую:
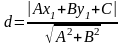 .
(5)
.
(5)
Найдем расстояние от точки М (16;-18) до прямой KL: .
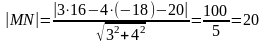 .
.
5) Медиана – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Для получения уравнения медианы KS необходимо найти координаты точки S – середины стороны LM . Координаты середины отрезка между точками и вычисляются по формулам:
 ,
,
 . (6)
. (6)
Тогда точка S будет иметь координаты:
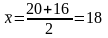 ,
,
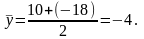
Таким образом, нам известны две точки K (−4;-8) и S (18; -4), через которые проходит прямая. Найдем уравнение прямой KS по формуле (2):
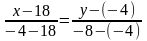 ,
,
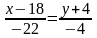 ,
,
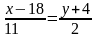 ,
,
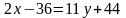 ,
,
 .
.
6) Точку пересечения F двух прямых MN и KS находится путем совместного решения уравнений этих прямых:
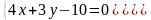 ,
,
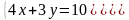 ,
,
 ,
,
 ,
,
 ,
,
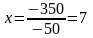 ,
,
 ,
т.е. F(7;-6).
,
т.е. F(7;-6).
7)
Площадь треугольника с вершинами
,
,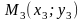 определяется по формуле
определяется по формуле
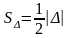 ,
где
,
где
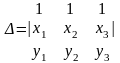 (7)
(7)
 ,
,
Тогда площадь треугольника KLM равна:

8) Уравнение окружности радиуса r с центром в точке Е(а; b) имеет вид:
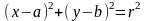 (8)
(8)
Так как MN является диаметром искомой окружности, то ее центр Е есть середина отрезка MN. Точка N – это точка пересечения прямых MN и KL. Найдем ее координаты путем совместного решения уравнений этих прямых.
 ,
,
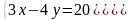 ,
,
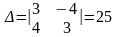 ,
,
 ,
,
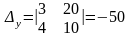 ,
,
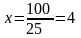 ,
,
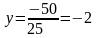 ,
т.е. N(4;-2)
,
т.е. N(4;-2)
Воспользовавшись формулами отыскания координат середины отрезка (6), получим координаты центра Е окружности, делящего диаметр MN пополам:
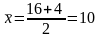 ,
,
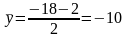 .
.
Следовательно,
Е
(10;-10) и
 .
Используя формулу (6), получаем уравнение
искомой окружности:
.
Используя формулу (6), получаем уравнение
искомой окружности:
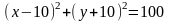 .
.
9) Множество точек треугольника KLM есть пересечение трех полуплоскостей, первая из которых ограничена прямой KL и содержит точку M, вторая ограничена прямой LM и содержит точку K, третья ограничена прямой KM и содержит точку L.
Для получения неравенства, определяющего полуплоскость, ограниченную прямой KL и содержащую точку M, подставим в уравнение прямой KL координаты точки M:
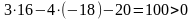 .
.
Поэтому
искомое неравенство имеет вид:
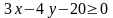 .
.
Для составления неравенства, определяющего полуплоскость, ограниченную прямой LM и содержащую точку K, найдем уравнение прямой LM, подставив в формулу (2) координаты точек L и M:
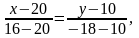
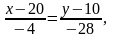
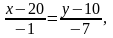
 ,
,
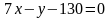 .
.
Подставив
в найденное уравнение координаты точки
K,
имеем:
 .
Искомое неравенство, определяющее
полуплоскость, ограниченную прямой LM
и содержащую точку K:
.
Искомое неравенство, определяющее
полуплоскость, ограниченную прямой LM
и содержащую точку K:
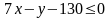 .
.
Чтобы найти неравенство, характеризующее полуплоскость, ограниченной прямой KM, содержащую точку L, найдем уравнение прямой KM, подставив координаты точек K и M в формулу (2):


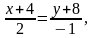
 ,
,
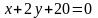 .
.
Подставляя
в последнее уравнение координаты точки
L,
получим:
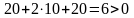 .
Тогда неравенство, определяющее
полуплоскость, ограниченную прямой KM,
содержащую точку L,
имеет вид:
.
Тогда неравенство, определяющее
полуплоскость, ограниченную прямой KM,
содержащую точку L,
имеет вид:
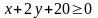 .
.
Таким образом, множество точек треугольника KLM определяется системой неравенств:
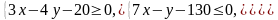
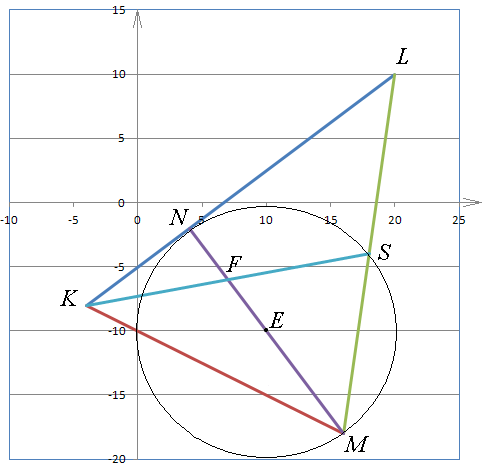
Задание 5
Найти:
1)
координаты центра и радиус окружности:
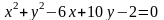 ;
;
2) каноническое
уравнение эллипса, проходящего через
точки
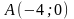 и
и

3) каноническое
уравнение гиперболы, если фокусное
расстояние равно 20,
а угловой коэффициент одной из асимптот
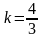 .
.
4) уравнение параболы с вершиной в начале координат, фокус которой расположен в точке F(0;-7).
Решение:
1)
Чтобы найти координаты центра и радиус
окружности, нужно данное уравнение
привести к уравнению вида
,
где a
и b
– координаты центра окружности С,
а r
– радиус. Для этого в исходном уравнении
следует выделить полные квадраты.
Сгруппируем одноименные переменные и
перепишем исходное уравнение следующим
образом:
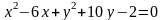 .
Дополним выражения
.
Дополним выражения
 и
и
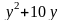 до полных квадратов, прибавив к первому
двучлену 9 и ко второму 25 и, чтобы выражение
левой части уравнения не изменилось,
из всего выражения вычтем эти же числа:
до полных квадратов, прибавив к первому
двучлену 9 и ко второму 25 и, чтобы выражение
левой части уравнения не изменилось,
из всего выражения вычтем эти же числа:
 .
Или, используя формулу квадрата суммы
или разности
.
Или, используя формулу квадрата суммы
или разности
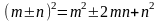 ,
запишем:
,
запишем:
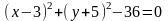 .
Таким образом, получим:
.
Таким образом, получим:
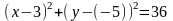 .
.
Отсюда,
координаты центра –
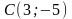 ,
а радиус окружности
,
а радиус окружности
 .
.
2)
Каноническое уравнение эллипса имеет
вид:
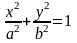 .
Задача сводится к определению параметров
а
и b.
Для этого подставим координаты известных
точек в уравнение эллипса. Точка А:
.
Задача сводится к определению параметров
а
и b.
Для этого подставим координаты известных
точек в уравнение эллипса. Точка А:
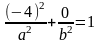 ,
,
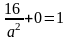 ,
отсюда
,
отсюда
 ,
,
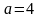 .
Зная параметр а,
подставим его и координаты точки В
в каноническое уравнение эллипса:
.
Зная параметр а,
подставим его и координаты точки В
в каноническое уравнение эллипса:
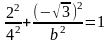 ,
или
,
или
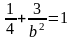 ,
отсюда
,
отсюда
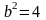 ,
или
,
или
 .
Подставляя найденные параметры а
и b
в уравнение эллипса, получим:
.
Подставляя найденные параметры а
и b
в уравнение эллипса, получим:
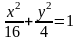
3)
Каноническое уравнение гиперболы имеет
вид:
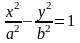 .
Задача сводится к нахождению параметров
а
и b.
Если расстояние между фокусами равно
20, то параметр
.
Задача сводится к нахождению параметров
а
и b.
Если расстояние между фокусами равно
20, то параметр
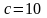 .
Уравнение асимптоты гиперболы в общем
случае имеет вид:
.
Уравнение асимптоты гиперболы в общем
случае имеет вид:
 ,
т.е. угловой коэффициент асимптоты
гиперболы
,
т.е. угловой коэффициент асимптоты
гиперболы
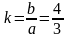 .
Параметры гиперболы a,
b,
и c
связаны соотношением
.
Параметры гиперболы a,
b,
и c
связаны соотношением
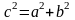 ,
но если, принять
,
но если, принять
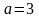 ,
а
,
а
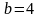 (что хотелось бы считать естественным),
то это соотношение выполняться не будет.
Это обусловлено тем, что при делении b
на а
происходит сокращение на некоторый их
общий множитель m,
т.е. угловой коэффициент прямой можно
представить в виде:
(что хотелось бы считать естественным),
то это соотношение выполняться не будет.
Это обусловлено тем, что при делении b
на а
происходит сокращение на некоторый их
общий множитель m,
т.е. угловой коэффициент прямой можно
представить в виде:
 ,
где
,
где
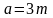 ,
а
,
а
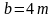 .
Таким образом, имеем:
.
Таким образом, имеем:
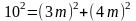 ,
или
,
или
 ,
отсюда
,
отсюда
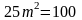 ,
т.е
,
т.е
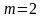 .
Тогда,
.
Тогда,
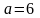 , а
, а
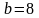 ,
и искомое каноническое уравнение
гиперболы имеет вид:
,
и искомое каноническое уравнение
гиперболы имеет вид:
 .
.
4)
Парабола с вершиной в начале координат,
фокус которой расположен в точке
 ,
симметрична относительно оси OY.
Уравнение такой параболы в общем случае
имеет вид:
,
симметрична относительно оси OY.
Уравнение такой параболы в общем случае
имеет вид:
 ,
а ее фокус имеет координаты
,
а ее фокус имеет координаты
 .
Задача сводится к нахождению параметра
p.
Из данных координат фокуса имеем:
.
Задача сводится к нахождению параметра
p.
Из данных координат фокуса имеем:
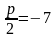 ,
отсюда
,
отсюда
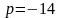 .
Тогда, подставив в уравнение параболы
найденный параметр p,
получим искомое уравнение параболы:
.
Тогда, подставив в уравнение параболы
найденный параметр p,
получим искомое уравнение параболы:
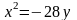 .
Полученная парабола обращена в
отрицательную сторону оси OY,
т.к.
.
Полученная парабола обращена в
отрицательную сторону оси OY,
т.к.
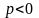 .
.
Задание 6.
Даны координаты
вершин пирамиды
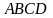 :
:
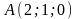 ,
,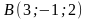 ,
,
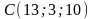 ,
,
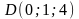 . Требуется: 1) записать векторы
. Требуется: 1) записать векторы
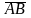 ,
,
 и
и
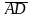 в системе орт и найти модули этих
векторов; 2) найти направляющие косинусы
векторов
,
и
;
3) найти угол
в системе орт и найти модули этих
векторов; 2) найти направляющие косинусы
векторов
,
и
;
3) найти угол
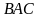 ;
4) найти проекцию вектора
на вектор
;
5) найти площадь грани
;
4) найти проекцию вектора
на вектор
;
5) найти площадь грани
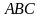 ;
6) найти объем пирамиды
;
7) найти длину высоты, опущенной из
вершины
;
6) найти объем пирамиды
;
7) найти длину высоты, опущенной из
вершины
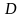 ;
8) найти координаты вершины Е
параллелограмма
;
8) найти координаты вершины Е
параллелограмма
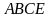 .
.
Решение:
1)
Произвольный вектор
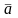 в системе орт
в системе орт
 ,
,
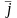 ,
,
 определяется следующей формулой:
определяется следующей формулой:
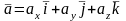 (1)
(1)
где
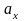 ,
,
 ,
,
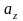 – проекции вектора
на координатные оси OX,
OY,
OZ,
называемые координатами вектора, а
,
,
– орты (единичные векторы), направление
которых совпадает с положительным
направлением осей OX,
OY,
OZ
соответственно. Если даны точки
– проекции вектора
на координатные оси OX,
OY,
OZ,
называемые координатами вектора, а
,
,
– орты (единичные векторы), направление
которых совпадает с положительным
направлением осей OX,
OY,
OZ
соответственно. Если даны точки
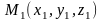 ,
,
 ,
то координаты вектора
,
то координаты вектора
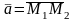 находятся по формулам:
находятся по формулам:
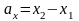 ,
,
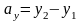 ,
,
 ,
(2)
,
(2)
т.е. из координат конца вектора вычитаются одноименные координаты начала. Тогда:
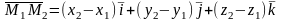 .
(3)
.
(3)
Подставив в (3) координаты точек А и В, получим вектор :
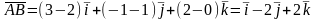 .
.
Аналогично, подставляя в (3) координаты точек А и С, находим:
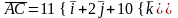 .
.
Подставив в (3) координаты точек А и D, находим вектор :
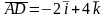
Если вектор задан формулой (1), то его модуль (длина) вычисляется по формуле:
 .
(4)
.
(4)
Применяя (4), получим модули векторов:
 ,
,
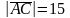 ,
,
 .
.
2) Косинусы углов, образованных вектором с положительным направлением осей координат (так называемые направляющие косинусы), определяются по формулам:
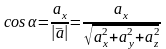 ,
,
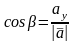 ,
,
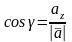 .
(5)
.
(5)
Зная координаты вектора и его модуль, вычислим для вектора направляющие косинусы:
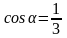 ,
,
 ,
,
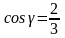 .
.
Аналогично,
запишем направляющие косинусы вектора
 :
:
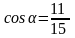 ,
,
 ,
,
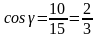 .
.
И, наконец, для вектора :
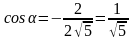 ,
,
 ,
,
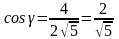 .
.
3)
Угол
– это угол между векторами
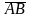 и
.
Косинус угла между векторами равен
скалярному произведению этих векторов,
деленному на произведение их длин:
и
.
Косинус угла между векторами равен
скалярному произведению этих векторов,
деленному на произведение их длин:
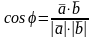 .
(6)
.
(6)
Найдем скалярное произведение векторов и по формуле:
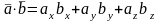 ,
(7)
,
(7)
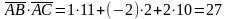 .
.
Модули
этих векторов уже найдены:
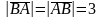 ,
.
Следовательно,
,
.
Следовательно,
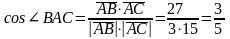 ,
тогда,
,
тогда,
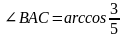 .
.
4) Проекция вектора на вектор равна скалярному произведению этих векторов, деленному на модуль вектора :
 .
.
5)
Площадь грани АВС
равна половине площади параллелограмма,
построенного на векторах
и
как на сторонах. Обозначим векторное
произведение вектора
на вектор
через вектор
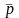 .
Тогда, как известно, длина вектора
численно равна площади параллелограмма,
построенного на векторах
и
,
а площадь грани АВС
будет равна половине модуля вектора
.
.
Тогда, как известно, длина вектора
численно равна площади параллелограмма,
построенного на векторах
и
,
а площадь грани АВС
будет равна половине модуля вектора
.
Векторное произведение двух векторов вычисляется по формуле:
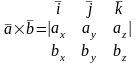 .
(8)
.
(8)
Тогда
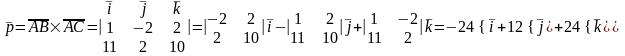 .
.
Отсюда, длина вектора , найденная по формуле (4), и площадь грани АВС равны:
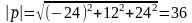 ,
,
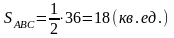 .
.
6) Объем треугольной пирамиды, построенной на трех некомпланарных векторах, равен абсолютной величине их смешанного произведения, деленной на шесть. Вычислим смешанное произведение трех векторов , и по формуле:
 .
(9)
.
(9)
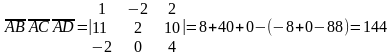 .
.
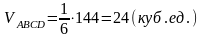 .
.
7)
Объем треугольной пирамиды можно также
найти по формуле:
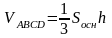 ,
где
,
где
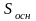 – площадь основания, т.е. площадь грани
АВС,
а h
– высота, опущенная из вершины D
на грань АВС.
Зная площадь грани АВС
– площадь основания, т.е. площадь грани
АВС,
а h
– высота, опущенная из вершины D
на грань АВС.
Зная площадь грани АВС
 и объем пирамиды ABCD
и объем пирамиды ABCD
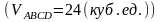 ,
вычислим длину высоты h:
,
вычислим длину высоты h:
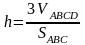 ,
,
 .
.
8)
Поскольку АВСЕ
– параллелограмм, то по правилу
параллелограмма сложения векторов
имеем:
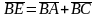 .
Найдем координаты векторов
.
Найдем координаты векторов
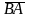 и
и
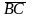 по формуле (2). Тогда получим:
по формуле (2). Тогда получим:
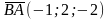 и
и
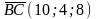 .
Суммой этих векторов является вектор
.
Суммой этих векторов является вектор
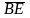 ,
координаты которого вычисляются путем
сложения одноименных координат векторов
и
,
т.е.
,
координаты которого вычисляются путем
сложения одноименных координат векторов
и
,
т.е.
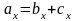 ,
,
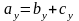 ,
,
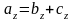 .
Таким образом, координаты вектора
:
–1+10=9, 2+4=6, –2+8=6, т.е.
.
Таким образом, координаты вектора
:
–1+10=9, 2+4=6, –2+8=6, т.е.
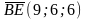 .
Зная координаты вектора
и точки B,
из формулы (2) можно найти координаты
точки Е
по формулам:
.
Зная координаты вектора
и точки B,
из формулы (2) можно найти координаты
точки Е
по формулам:
 ,
,
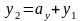 ,
,
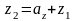 ,
(10)
,
(10)
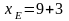 ,
,
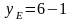 ,
,
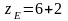 .
.
Итак,
точка Е
имеет координаты:
 .
.
Задание 1
Решить систему линейных алгебраических уравнений по правилу Крамера:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание 2
Решить систему линейных алгебраических уравнений матричным способом:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание 3
Решить систему линейных алгебраических уравнений методом Гаусса, провести исследование с помощью теоремы Кронекера-Капелли:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание 4
Даны вершины треугольника ABC. Построить треугольник на координатной плоскости и найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) внутренний угол А; 4) уравнение высоты CD и ее длину; 5) уравнение медианы АЕ; 6) точку пересечения высоты CD и медианы АЕ; 7) площадь треугольника АВС; 8) уравнение окружности, для которой высота CD есть диаметр; 9) систему линейных неравенств, определяющих треугольник ABC.
-
А ( -5; 0 ),
В ( 7; 9),
С ( 5; - 5).
А ( -7; 2 ),
В ( 5; 11),
С ( 3; -3).
А ( -5; -3 ),
В ( 7; 6 ),
С ( 5; -8).
А ( -6; -2 ),
В ( 6; 7 ),
С ( 4; - 7 ).
А ( -8; -4 ),
В ( 4; 5 ),
С ( 2; - 9 ).
А ( 0; -1 ),
В ( 12; 8 ),
С ( 10; -6 ).
А ( -6; 1 ),
В ( 6; 10 ),
С ( 4; -4 ).
А ( -2; -4 ),
В ( 10; 5 ),
С ( 8; -9 ).
А ( -3; 0 ),
В ( 9; 9 ),
С ( 7; 5 ).
А ( -9; -2 ),
В ( 3; 7 ),
С ( 1; -7 ).
А ( -5; 2 ),
В ( 7; -7 ),
С ( 5; 3 ).
А ( -7; 5 ),
В ( 5; -4 ),
С ( 3; 10 ).
А ( -7; 1 ),
В ( 5; -8 ),
С ( 3; 6 ).
А ( 0; 3 ),
В ( 12; -6 ),
С ( 10; 8 ).
А ( -8; 4 ),
В ( 4; -5 ),
С ( 2; 9 ).
А ( -2; 2 ),
В ( 10; -7 ),
С ( 8; 7 ).
А ( 1; 2 ),
В ( 13; -7 ),
С ( 11; 7 ).
А ( -4; 1),
В ( 8; -8 ),
С ( 6; 6 ).
А ( -7; -1 ),
В ( -5; -10 ),
С ( 3; 4 ).
А ( -3; 3 ),
В ( 9; -6 ),
С ( 7; 8 ).
Задание 5
Найти:
1)
координаты центра и радиус окружности
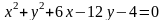 ;
;
2)
каноническое уравнение эллипса, малая
полуось которого равна
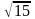 ,
а эксцентриситет
,
а эксцентриситет
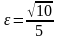 ;
;
3) каноническое уравнение гиперболы,
расстояние между вершинами которой
равно 16, а одна из асимптот имеет угловой
коэффициент
 ;
;
4) уравнение параболы с вершиной в начале
координат, симметричной относительно
оси ОХ и проходящей через точку
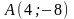 .
.
Найти:
1)
координаты центра и радиус окружности
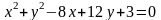 ;
;
2)
каноническое уравнение эллипса,
малая полуось которого равна 2, а фокус
находится в точке
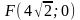 ;
;
3)
каноническое уравнение гиперболы,
действительная полуось которой равна
7, а эксцентриситет
 ;
;
4)
уравнение параболы с вершиной в начале
координат, директрисой которой является
прямая
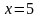 .
.
Найти:
1)
координаты центра и радиус окружности
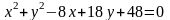 ;
;
2)
каноническое уравнение эллипса, который
проходит через точки
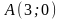 и
и
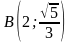 ;
;
3) каноническое уравнение гиперболы, одна из вершин которой находится в точке , а одна из асимптот имеет угловой коэффициент ;
4)
уравнение параболы с вершиной в начале
координат, директрисой которой является
прямая
 .
.
Найти:
1)
координаты центра и радиус окружности
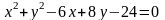 ;
;
2)
каноническое уравнение эллипса, который
проходит через точку
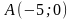 и имеет эксцентриситет
и имеет эксцентриситет
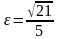 ;
;
3)
каноническое уравнение гиперболы,
проходящей через точки
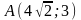 и
и
 ;
;
4)
уравнение параболы с вершиной в начале
координат, директрисой которой является
прямая
 .
.
Найти:
1)
координаты центра и радиус окружности
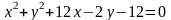 ;
;
2)
каноническое уравнение эллипса, большая
ось которого равна 22, а эксцентриситет
 ;
;
3)
каноническое уравнение гиперболы,
фокусное расстояние которой равно
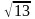 ,
а одна из асимптот имеет угловой
коэффициент
,
а одна из асимптот имеет угловой
коэффициент
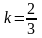 ;
;
4)
уравнение параболы с вершиной в начале
координат, симметричной относительно
оси ОХ
и проходящей через точку
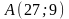 .
.
Найти:
1)
координаты центра и радиус окружности
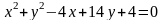 ;
;
2) каноническое уравнение эллипса, малая полуось которого равна , а эксцентриситет ;
3) каноническое уравнение гиперболы, расстояние между вершинами которой равно 16, а одна из асимптот имеет угловой коэффициент ;
4)
уравнение параболы с вершиной в начале
координат, симметричной относительно
оси ОХ
и проходящей через точку
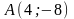 .
.
Найти:
1)
координаты центра и радиус окружности
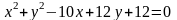 ;
;
2)
каноническое уравнение эллипса, большая
полуось которого равна 5, а фокус находится
в точке
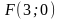 ;
;
3)
каноническое уравнение гиперболы,
мнимая полуось которой равна
 ,
а фокус находится в точке
,
а фокус находится в точке
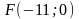 ;
;
4) уравнение параболы с вершиной в начале
координат, фокус которой находится в
точке
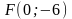 .
.
Найти:
1)
координаты центра и радиус окружности
 ;
;
2)
каноническое уравнение эллипса, малая
полуось которого равна
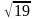 ,
а фоку
,
а фоку
с
находится в точке
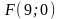 ;
;
3)
каноническое уравнение гиперболы,
действительная полуось которой равна
5, а эксцентриситет
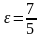 ;
;
4)
уравнение параболы с вершиной в начале
координат, фокус которой находится в
точке
 .
.
Найти:
1)
координаты центра и радиус окружности
 ;
;
2)
каноническое уравнение эллипса, который
проходит через точки
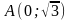 и
и
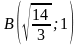 ;
3) каноническое уравнение гиперболы,
один из фокусов которой находится в
точке
,
а одна из асимптот имеет угловой
коэффициент
;
3) каноническое уравнение гиперболы,
один из фокусов которой находится в
точке
,
а одна из асимптот имеет угловой
коэффициент
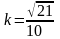 ;
;
4) уравнение параболы с вершиной в начале координат, фокус которой находится в точке .
Найти:
1)
координаты центра и радиус окружности
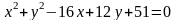 ;
;
2)
каноническое уравнение эллипса, который
проходит через точку
 и имеет эксцентриситет
и имеет эксцентриситет
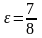 ;
;
3)
каноническое уравнение гиперболы,
которая проходит через точки
и
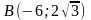 ;
;
4)
уравнение параболы с вершиной в начале
координат, директрисой которой является
прямая
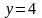 .
.
Найти:
1)
координаты
центра и радиус окружности
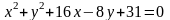 ;
;
2)
каноническое уравнение эллипса, большая
ось которого равна 24, а эксцентриситет
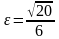 ;
;
3)
каноническое уравнение гиперболы,
мнимая полуось которой равна 3, а фокус
находится в точке
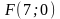 ;
;
4)
уравнение параболы с вершиной в начале
координат, симметричной относительно
оси ОХ
и проходящей через точку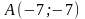 .
.
Найти:
1)
координаты центра и радиус окружности
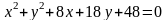 ;
;
2)
каноническое уравнение эллипса, малая
полуось которого равна 2, а эксцентриситет
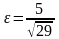 ;
;
3)
каноническое уравнение гиперболы,
расстояние между вершинами которой
равно 26, а одна из асимптот имеет угловой
коэффициент
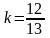 ;
;
4)
уравнение параболы с вершиной в начале
координат, симметричной относительно
оси ОХ
и проходящей через точку
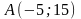 .
.
Найти:
1) координаты центра и радиус окружности
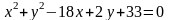 ; 2
; 2
2) каноническое уравнение эллипса,
большая полуось которого равна 6, а фокус
находится в точке
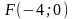 ;
;
3) каноническое уравнение гиперболы,
фокусное расстояние которой равно
 ,
а одна из асимптот имеет угловой
коэффициент
,
а одна из асимптот имеет угловой
коэффициент
 ;
;
4) уравнение параболы с вершиной в начале
координат, директрисой которой является
прямая
 .
.
Найти:
1)
координаты центра и радиус окружности
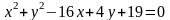 ;
;
2)
каноническое уравнение эллипса, малая
полуось которого равна 7, а фокус находится
в точке
 ;
;
3)
каноническое уравнение гиперболы,
действительная полуось которой равна
11, а эксцентриситет
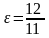 ;
;
4)
уравнение параболы с вершиной в начале
координат, фокус которой находится в
точке
 .
.
Найти:
1)
координаты центра и радиус окружности
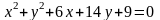 ;
;
2)
каноническое уравнение эллипса, который
проходит через точки
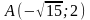 и
и
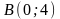 ;
;
3)
каноническое уравнение гиперболы, одна
из вершин которой находится в точке
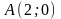 ,
а одна из асимптот имеет угловой
коэффициент
,
а одна из асимптот имеет угловой
коэффициент
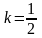 ;
;
4)
уравнение параболы с вершиной в начале
координат, директрисой которой является
прямая
 .
.
Найти:
1)
координаты центра и радиус окружности
 ;
;
2)
каноническое уравнение эллипса, который
проходит через точку
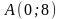 и имеет эксцентриситет
и имеет эксцентриситет
 ;
;
3)
каноническое уравнение гиперболы,
которая проходит через точки
 и
и
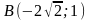 ;
;
4)
уравнение параболы с вершиной в начале
координат, директрисой которой является
прямая
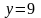 .
.
Найти:
1)
координаты центра
и радиус окружности
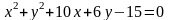 ;
;
2)
каноническое уравнение эллипса, большая
ось которого равна 22, а эксцентриситет
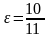 ;
;
3)
каноническое уравнение гиперболы,
фокусное расстояние которой равно
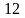 ,
а одна из асимптот имеет угловой
коэффициент
,
а одна из асимптот имеет угловой
коэффициент
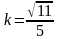 ;
;
4)
уравнение параболы с вершиной в начале
координат, симметричной относительно
оси ОХ
и проходящей через точку
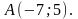
Найти:
1)
координаты центра и радиус окружности
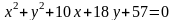 ;
;
2)
каноническое уравнение эллипса, малая
полуось которого равна 5, а эксцентриситет
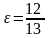 ;
;
3)
каноническое уравнение гиперболы,
мнимая полуось которой равна 6, а фокус
находится в точке
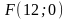 ;
;
4)
уравнение параболы с вершиной в начале
координат, симметричной относительно
оси ОУ и проходящей через точку
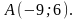
Найти:
1)
координаты центра и радиус окружности
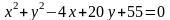 ;
;
2) каноническое уравнение эллипса, большая полуось которого равна 9, а фокус находится в точке ;
3)
каноническое уравнение гиперболы,
расстояние между вершинами которой
равно 6, а одна из асимптот имеет угловой
коэффициент
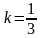 ;
;
4)
уравнение параболы с вершиной в начале
координат, директрисой которой является
прямая
 .
.
Найти:
1)
координаты центра и радиус окружности
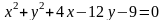 ;
;
2)
каноническое уравнение эллипса, малая
полуось которого равна 5, а фокус находится
в точке
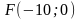 ;
;
3)
каноническое уравнение гиперболы,
действительная полуось которой равна
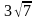 ,
а эксцентриситет
,
а эксцентриситет
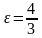 ;
;
4)
уравнение параболы с вершиной в начале
координат, директрисой которой является
прямая
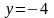 .
.
Задание 6
Даны координаты вершин пирамиды . Требуется: 1) записать векторы , и в системе орт и найти модули этих векторов; 2) найти направляющие косинусы векторов , и ; 3) найти угол ; 4) найти проекцию вектора на вектор ; 5) найти площадь грани ; 6) найти объем пирамиды ; 7) найти длину высоты, опущенной из вершины ; 8) найти координаты вершины Е параллелограмма .
|
|
А (2; -3;1), |
В ( 6;1;-1), |
С ( 4;8;-9), |
D (2;-1;2). |
|
|
А (5; -1;-4), |
В ( 9;3;-6), |
С ( 7;10;-14), |
D (5;1;-3). |
|
|
А (1; -4;0), |
В ( 5;0;-2), |
С ( 3;7;-10) |
D (1;-2;1). |
|
|
А (-3;-6;2), |
В ( 1;-2;0), |
С ( -1;5;-8), |
D (-3;-4;3). |
|
|
А (-1;1;-5), |
В ( 3;5;-7), |
С ( 1;12;-15), |
D (-1;3;-4). |
|
|
А (-4;2;-1), |
В (0;6;-3), |
С (-2;13;-11), |
D (-4;4;0). |
|
|
А (0;4;3), |
В (4;8;1), |
С (2;15;-7), |
D (0;6;4). |
|
|
А (-2;0;-2), |
В (2;4;-4), |
С (0;11;-12), |
D (-2;2;-1). |
|
|
А (3;3;-3), |
В (7;7;-5), |
С (5;14;-13), |
D (3;5;-2). |
|
|
А (4;-2;5), |
В (8;2;3), |
С (6;9;-5), |
D (4;0;6). |
|
|
А (-5;0;1), |
В (-4;-2;3), |
С (6;2;11), |
D (3;4;9). |
|
|
А (1;-4;0), |
В (2;-6;2), |
С (12;-2;10), |
D (9;0;8). |
|
|
А (-1;-2;-8), |
В (0;-4;-6), |
С (10;0;2), |
D (7;2;0). |
|
|
А (0;2;-10), |
В (1;0;-8), |
С (11;4;0), |
D (8;6;-2). |
|
|
А (3;1;-2), |
В (4;-1;0), |
С (14;3;8), |
D (11;5;6). |
|
|
А (-8;3;-1), |
В (-7;1;1), |
С (3;5;9), |
D (0;7;7). |
|
|
А (2;-1;-4), |
В (3;-3;-2), |
С (13;1;6), |
D (10;3;4). |
|
|
А (-4;5;-5), |
В (-3;3;-3), |
С (7;7;5), |
D (4;9;3). |
|
|
А (-2;-3;2), |
В (-1;-5;4), |
С (9;-1;12), |
D (6;1;10). |
|
|
А (-3;4;-3), |
В (-2;2;-1), |
С (8;6;7), |
D (5;8;5). |

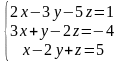 ;
;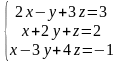 ;
;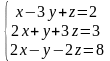 ;
; ;
;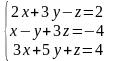 ;
;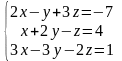 ;
;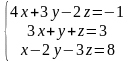 ;
;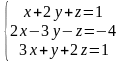 ;
; ;
;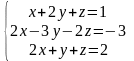 ;
;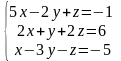 ;
;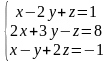 ;
;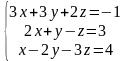 ;
;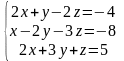 ;
; ;
;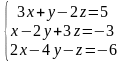 ;
;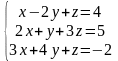 ;
;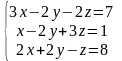 .
. ;
;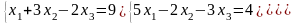 ;
;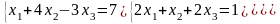 ;
;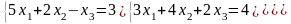 ;
;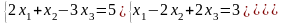 ;
;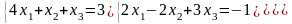 ;
;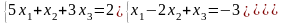 ;
;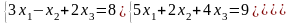 ;
;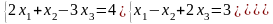 ;
;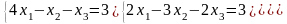 ;
; ;
;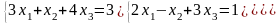 ;
;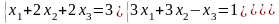 ;
;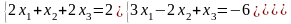 ;
; ;
;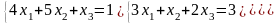 ;
;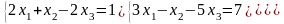 ;
;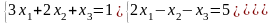 ;
;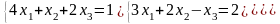 ;
;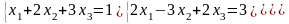 .
.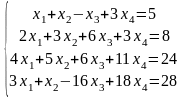 ;
;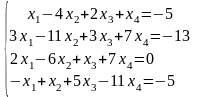 ;
;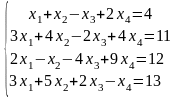 ;
;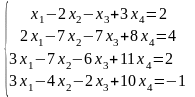 ;
;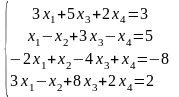 ;
;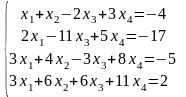 ;
; ;
;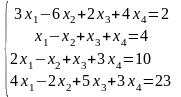 ;
; ;
;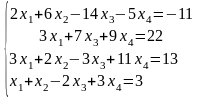 ;
;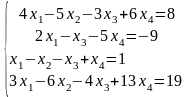 ;
; ;
;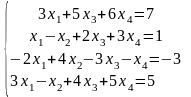 ;
;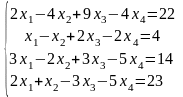 ;
;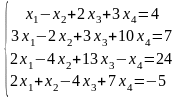 ;
;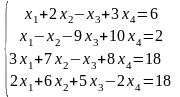 ;
;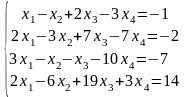 ;
;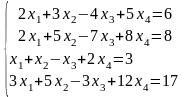 ;
;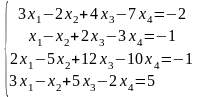 ;
;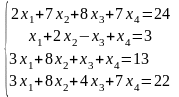 .
.