Фирма, или предприятие, - экономический агент, принимающий решения о производстве благ на продажу с использованием ресурсов, приобре­таемых на рынке. Из этого определения видно, что фирма как институт го­раздо моложе домохозяйства. Этот институт появился как раз за счет отпоч­кования от домохозяйства процессов производства благ. Часть этих благ представляет собой предметы потребления, покупаемые домохозяйствам.

Теории поведения фирмы

В них утверждается, что при несовершенных рынках капитала и неконкурентных рынках управляющие могут стремиться к достижению целей, отличных от максимизации прибыли.

По мнению некото­рых исследователей (Г. Саймон, Р. М. Сайерт, Дж. Г. Марч, С. Винтер), целью фирмы является максимизация не прибыли, а объема продаж.

Взгляды этих экономистов представляют так называемые поведенческие теории фирмы. Американский экономист Г. Саймон, получивший в 1978 г. Нобелевскую премию за исследование поведения фирмы, выдвинул теорию удовлетворения, согласно которой фирма стремится достичь оп­ределенного уровня прибыли, а далее не предпринимает усилий, чтобы ее максимизировать. В этом случае и количество продукции, которое она выпускает, не обеспечивает получения максимальной прибыли. Объясняя поведение фирмы на основе своей теории, Г. Саймон приходит к заключе­нию, что "целью фирмы является не максимизация, а достижение опреде­ленного уровня прибыли, удержание определенной доли рынка и опреде­ленного объема продаж. Фирмы стремятся достичь скорее удовлетворения, чем максимизации.

Существует также эволюционная теория, в соответствии с которой фирмы могут только стремиться, но никогда не получают максимальной прибыли, так как они функционируют в мире неполной, порой искаженной информации, в постоянно меняющихся условиях, на которые им очень трудно адекватно реагировать. По мнению сторонников этой теории, на практике фирмы главным образом направляют свои усилия на то, чтобы получить определенную долю на рынке и удержать ее, а не на то, чтобы выйти на новый или покинуть завоеванный рынок. Такое поведение фирм С. Винтер характеризует как "рутинное". Фирмы меняют рутинный характер

если их вынуждают обстоятельства; тогда они делают инновации, для которых нужна прибыль.

И все же в неоклассическом экономическом анализе и в учебниках эко­номики теория фирмы построена на предположении о стремлении фирмы максимизировать общую сумму своей прибыли. Основываясь на этой предпосылке (а она подтверждается практикой), можно описать поведение фирмы и научно обосновать принимаемые ею решения. Функция максимизации прибыли выполняется за счет получения как можно большей раз­ницы между доходами и издержками фирмы.

Производственная функция с двумя переменными факторами. Изокванта

В предыдущих рассуждениях мы рассмотрели производствен­ную функцию, которая зависела от одного переменного фактора, в то время как остальные оставались неизменными.

Рассмотрим вариант, когда переменными являются два фак­тора производства, которые при определенном сочетании дают в результате один объем производимого продукта. Возьмем, например, затраты труда и капитала при производстве обуви. Затраты труда обозначим за X, затраты капитала — через У. При определенной комбинации этих двух факторов может быть произведено 200 пар обуви (Q = 200). Изменение капитала и труда может происходить в обратном направлении. Если ко­личество капитала (применяемого оборудования) увеличивается, то, следовательно, применение живого труда — уменьшается. При этом возрастание одного фактора и уменьшение друго­го происходят таким образом, что общий объем производства остается на прежнем уровне.

Эту зависимость можно представить графически с использо­ванием изокванты (рис. ).

Рис. Изокванта, отражающая производственную функ­цию с двумя переменными факторами

Изокванта, или кривая равного продукта, отражает все возможные комбинации двух факторов, которые могут быть использованы для производства определенного объема продукта.

С увеличением объемов используемых переменных факторов, возникает возможность выпуска большего объема продукции. Изо­кванта, отражающая производство большего объема продукта, бу­дет расположена правее и выше предыдущей изокванты.

Количество использованных факторов х и у может постоян­но меняться, соответственно будет уменьшаться или увеличи­ваться максимальный выпуск продукта. Следовательно, может возникнуть множество изоквант, соответствующих разным объ­емам выпускаемой продукции, которые образуют карту изоквант

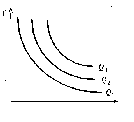
Рис. Карта изоквант

Изокванты являются подобием кривых безразличия с той лишь разницей, что они отражают ситуацию не в сфе­ре потребления, а в сфере производства. То есть изо­кванты обладают свойствами, близкими кривым безразли­чия.

Отрицательный наклон изо­квант объясняется тем, что увеличение использования од­ного фактора при определен­ном объеме выпуска продукта всегда будет сопровождаться уменьшением количества другого фактора.

Если в нашем примере с производством обуви происходит уве­личение применяемого капитала в виде оборудования, то, следо­вательно, меньше труда рабочих необходимо будет использовать Для производства определенного количества продукта.

Так же как кривые безразличия, расположенные на разном расстоянии от начала координат, характеризуют разный уровень полезности для потребителя, так и изокванты дают информацию о разных уровнях выхода продукции.

Возникает вопрос, на сколько нужно увеличить объем капи­тала (фактор у), чтобы уменьшить на одного человека приме­нение живого труда (фактор х) при заданном объеме выпуска продукции? Чтобы ответить нужно рассмотреть крутизну на­клона изокванты, который характеризуется предельной Нормой технологического замеще­ния (МRТS_XY).

Предельная норма технологического замещения измеряется соотношением изменения фактора у к изменению фактора х. Поскольку замена факторов происходит в обратном отношении, то математическое выражение показателя МRТS_XY берется со знаком минус:

Если мы возьмем какую-либо точку на изокванте, например, точку А (рис. ) и проведем к ней касательную КМ, то тангенс угла даст нам значение

МRТS_XY.

Можно отметить, что в верхней части изокванты угол будет достаточно велик, что говорит о том, что для изменения факто­ра х на единицу требуются значительные изменения фактора у. Следовательно, в этой части кривой значение МRТS_XY будет велико.

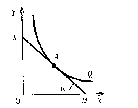
Рис. Определение нормы технологического замеще­ния через касательную к изокванте

По мере движения вниз по изокванте значение предельной нормы технологического замещения будет постепенно убывать Это означает, что для увеличения фактора х на единицу потребуется незначительное уменьшение фактора у.

Рис. 69. Изменение МRТS_XY при движении вниз по изокванте

На рисунке видно, что при переходе от точки А к точке В и при увеличении фактора х на единицу необходимо фактор у уменьшить на две единицы, то есть МRТS_XY = —2.

Если мы опустимся по изокванте и перейдем от точки С к точке D (при этом фактор х увеличится также, как и в предыдущем случае, на единицу), то фактор у в этом случае уменьшится на 0,5 и МRТS_XY = —0, 5.

В реальных производственных процессах встречается два исключительных случая в конфигурации изоквант. Это ситуа­ция, когда два переменных фактора идеально взаимозаменяемы, и случай, когда они жестко взаимодополняют друг друга. В первом случае (рис.) при полной заменяемости факторов производства МRТS_XY = const.

Рис. Изокванта при полной заменяемости факторов

Подобную ситуацию можно представить при возможности полной автоматизации производ­ства. Тогда в точке А весь процесс производства будет состоять из затрат капитала. В точке В все машины будут заменены рабочими руками, а в точках С и О капитал и труд будут дополнять друг друга.

В ситуации с жесткой дополняемостью факторов (рис. ) предельная норма технологического замещения будет равна 0 (МRТS_XY = 0).

Рис. Изокванта при жесткой дополняемости факторов

Если мы возьмем современный таксопарк с постоянным количеством машин (у1), для работы на которых необходимо определенное количество водителей (х1), то можно сказать, что количество обслуживаемых пассажиров в течение суток не увеличится, если мы увеличим численность водитель­ского состава до х2, х3,... хn. Объем производимого продукта увеличится с Q1 до Q2 только в том случае, если увеличится количество используемых машин в таксопарке и численность водителей.