
- •Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
- •Двойное проницание
- •1. Цель и содержание задания
- •2. Порядок выполнения задания
- •3. Методические указания к выполнению задания "двойное проницание"
- •1. Цель и содержание задания ……………………………………………...1
- •2. Порядок выполнения задания ……………………………………………1
3. Методические указания к выполнению задания "двойное проницание"
3.1. Проецирование геометрического тела.
По двум неполным проекциям полого геометрического тела (рис.1)
1. достроить вторую неполную проекцию;
2. построить третью проекцию по двум имеющимся;
3. выполнить полезные разрезы и заданный горизонтальный разрез;
4. построить диметрическое изображение детали.
Рассмотрим графическое условие задачи,
приведенной
на рис. 1. Геометрическое тело представляет
собой усеченный конус с соосным с ним
сквозным цилиндрическим отверстием.
Кроме того в этом геометрическом теле
имеется сквозное призматическое
отверстие, ограниченное двумя
горизонтальными и двумя профильными
плоскостями уровня. Горизонтальная
проекция не достроена: на поверхности
конуса не показаны линии выхода призмы.
Для отыскания этих выходов проводят
горизонтальные плоскости
![]() и
и
![]() (рис. 2), которые пересекают конус по
окружностям радиусов
(рис. 2), которые пересекают конус по
окружностям радиусов
![]() и
и
![]() соответственно.
На этих окружностях определяются
горизонтальные проекции точек 1,2,5,6
и 3,4,7,8.
соответственно.
На этих окружностях определяются
горизонтальные проекции точек 1,2,5,6
и 3,4,7,8.

Рис. 1. Графическое условие задачи
4


Рис. 2. Проецирование геометрического тела с вырезами
Профильные плоскости, ограничивающие слева и справа призматическое отверстие, пересекают конус по двум гиперболам. На виде сверху эти гиперболы с проецируются также в прямые линии, как и на виде спереди. А на профильной плоскости проекций гиперболы должны быть построены по отдельным точкам. Дополнительно к имеющимся точкам 1, 2, 3, 4, 5, 6, 7, 8 воспользуемся заданной горизонтальной плоскостью АА, которая дает еще четыре точки 9, 10, 11, 12. Этих точек достаточно для построения профильной проекции обеих гипербол.
Внутренний цилиндр полностью пересекается верхней и нижней гранями призмы, в результате чего получаются две окружности. Эти окружности проецируются на фронтальную и профильную плоскости проекций в виде отрезков прямых линий, а на горизонтальную в уже имеющуюся окружность радиуса R.
5
На профильную плоскость проекций усеченный конус спроецируется точно так же, как и на фронтальную, внутренний соосный цилиндр также не изменится. Третью проекцию призматического отверстия следует строить по отдельным точкам, уже имеющимся на чертеже. Так, например, для построения профильных проекций точек 1 и 2 достаточно взять расстояние от горизонтальной оси симметрии до точки 1 (2) и отложить его по линии связи от оси конуса в обе стороны (помечено фигурными скобками). Остальные точки строятся аналогично.
На виде спереди выполнен фронтальный разрез. Так как секущая плоскость совпала с плоскостью симметрии, то оставлена только половина фронтального разреза, причем, секущая плоскость не обозначена и разрез не подписан. Отделен вид спереди от фронтального разреза линией штрихпунктирной, т.е. осью симметрии.
Исходя из аналогичных рассуждений выполнен и профильный разрез Горизонтальный же разрез А А обозначен и отделен от половины вида сверху тоже штрихпунктирной линией.
3.2.
Построение аксонометрического изображения
детали.
Рис. 3. Аксонометрические оси и коэффициенты искажения в прямоугольной диметрии
В
прямоугольной диметрии по осям Х' и Z'
коэффициенты искажения равны, а по
![]()
в два раза меньше. Углы между
аксонометрическими осями показаны на
рис. 3.
в два раза меньше. Углы между
аксонометрическими осями показаны на
рис. 3.
Теоретически выведено, что коэффициенты искажения по осям X' и Z' равны 0,94, а по оси = 0,47. Пользоваться такими коэффициентами очень неудобно, поэтому строят рекомендованную ГОСТ 2.31769 стандартную прямоугольную диметрию без искажения размеров по осям Х' и Z' и с уменьшением в два раза по оси Y'(то есть принимают вместо теоретически выведенных коэффициентов 1 и 0,5 соответственно).
6
Изображение предмета, построенного в стандартной диметрии, получается увеличенным в 1,06 раза (1/0,94) по сравнению с действительными размерами.
На рис 4 показано положение эллипсов в прямоугольной диметрии и величина их большой и малой осей.
Большие оси всех эллипсов одинаковы и равны 1,06d окружности По направлению они перпендикулярны продолжению свободных осей. Малые оси двух эллипсов, расположенных в горизонтальной и профильной плоскостях проекций, равны 0,35d, а во фронтальной плоскости 0,95d окружности. Направление их совпадает с направлением свободных ("отсутствующих") осей.

Рис. 4. Изображение окружностей в прямоугольной диметрии
Чтобы построить в диметрии какую – либо плоскую фигуру, например, пятиугольник, предварительно распределяют на нем положение координатных осей. Удобно совмещать координатные оси с осями симметрии фигуры, если таковые имеются (рис.5а)

Рис. 5. Изображение пятиугольника в прямоугольной диметрии
7
Затем проводят аксонометрические оси х', у'( рис.5,б). Из точки О' вверх по оси у' откладывают отрезок O'A', равный по величине 0,5 отрезка АО, затем откладывают отрезок 0'М'=0,5 ОМ. От точки 0' вниз откладывают отрезок O'N'=0,5 ON. Через полученные точки N' и М' проводят прямые, параллельные оси X'. На этих прямых от точек М' и N' в обе стороны откладывают отрезки, равные отрезкам ВМ, ME, СN , ND соответственно. Полученные точки А', В', C', D' ,E' соединяют. Получили диметрическое изображение пятиугольника, расположенного в горизонтальной плоскости проекций. На рис. 5, в изображен пятиугольник, расположенный во фронтальной плоскости проекций, а на рис.5, г пятиугольник в профильной плоскости проекций.
Для получения наглядного изображения геометрического тела в прямоугольной диметрии поступают следующим образом. Вначале проводят на ортогональных проекциях координатные оси. Так как деталь симметричная, координатные оси совмещают с осями ее симметрии (рис.2).
Затем
проводят аксонометрические оси x',
y',
z'
(рис.6)
и приступают к построению
аксонометрии,
начиная с нижнего основания конуса.
Строят эллипс так, как показано на
рис.4,а.
Верхнее и нижнее основание конуса,
как
и оба основания внутреннего цилиндрического
отверстия, расположены в плоскостях,
параллельных плоскости Н. Поэтому
большие оси эллипсов, в которые
спроецируются окружности оснований,
будут расположены перпендикулярно оси
Z',
а
малые оси совпадут по направлению с
этой осью. Центры нижнего основания
конуса и цилиндра расположены в точке
![]() .
Через эту точку проводят прямую,
перпендикулярную оси Z',
на
ней откладывают большие оси обоих
эллипсов, равные по величине 1,06 диаметра
нижнего основания конуса и 1,06 диаметра
цилиндра. Малые оси составляют 0,35
соответствующих диаметров. По оси
.
Через эту точку проводят прямую,
перпендикулярную оси Z',
на
ней откладывают большие оси обоих
эллипсов, равные по величине 1,06 диаметра
нижнего основания конуса и 1,06 диаметра
цилиндра. Малые оси составляют 0,35
соответствующих диаметров. По оси
![]() откладывают диаметры окружностей
оснований без искажения, а по оси
откладывают диаметры окружностей
оснований без искажения, а по оси
![]()
те же диаметры, уменьшенные в два раза
(коэффициент искажения по оси у' = 0,5).
те же диаметры, уменьшенные в два раза
(коэффициент искажения по оси у' = 0,5).

Рис. 6. Построение диметрии геометрического тела с вырезами
Для построения верхнего основания конуса от точки 0'1 откладывают отрезок, равный высоте конуса. В полученной точке 0'4 располагаются центры верхнего основания конуса и внутреннего цилиндрического отверстия. Строят эти два эллипса, как было описано выше. Затем проводят очерковые образующие геометрических тел.
После этого приступают к вычерчиванию призматического выреза. Горизонтальные плоскости уровня, ограничивающие сверху и снизу призматическое отверстие, пересекают внутренний цилиндр полностью, при этом получаются две окружности с центрами в точках 0'2 и 0'3 , диаметры окружностей одинаковы и равны диаметру цилиндра.
Эти же плоскости пересекают и конус также по окружностям, но уже разных диаметров. Центры этих окружностей совпадают с центрами O'2 и O'3
Чтобы построить выше указанные окружности в диметрии, необходимо на аксонометрическом изображении (рис.6) от точки 0'1 отложить вверх отрезки, равные отрезкам O1O2 и O1O3 . В полученных точках O'2 и O'3 строят эллипсы, как показано выше.
Далее приступают к построению гипербол, которые получаются при пересечении конуса с двумя профильными плоскостями уровня. Строят их по отдельным точкам.
Так
как точки 1, 2, 5, 6 лежат на окружности,
принадлежащей конусу и имеющей центр
в точке![]() ,
то построить в диметрии эти точки просто.
Достаточно от точки O'3
по
оси X'3
в
обе стороны отложить отрезки, равные
17 мм, а через полученные точки провести
прямые, параллельные оси У'3.
Эти
прямые засекут на внешнем эллипсе точки
1, 2, 5, 6 . Точки 3,4, 7, 8 строятся аналогично.
Для построения гиперболы следует
воспользоваться секущей плоскостью
АА,
выполнив построения в описанной выше
последовательности. Получим точки 9,
10, 11, 12, через которые пройдут ветви
гиперболы.
,
то построить в диметрии эти точки просто.
Достаточно от точки O'3
по
оси X'3
в
обе стороны отложить отрезки, равные
17 мм, а через полученные точки провести
прямые, параллельные оси У'3.
Эти
прямые засекут на внешнем эллипсе точки
1, 2, 5, 6 . Точки 3,4, 7, 8 строятся аналогично.
Для построения гиперболы следует
воспользоваться секущей плоскостью
АА,
выполнив построения в описанной выше
последовательности. Получим точки 9,
10, 11, 12, через которые пройдут ветви
гиперболы.
Построив диметрическое изображение детали в тонких линиях, вырезают одну четвертую часть ее и наносят штриховку. Для построения выреза в детали проводят две секущие плоскости: одну через ocи Z' и X'1, а другую через оси Z' и У'1. Первая секущая плоскость разрезает деталь по замкнутому многоугольнику. ABCDEFGH, а вторая по многоугольникам NMQP и TASK.
Д алее
следует нанести штриховку. Линии
штриховки наносят параллельно одной
из диагоналей проекций квадратов,
лежащих в соответствующих координатных
плоскостях, стороны которых параллельны
аксонометрическим осям ( ГОСТ 2.31769,
СТ СЭВ 197979).
На рис. 7 показано направление штриховки
в диметрии.
алее
следует нанести штриховку. Линии
штриховки наносят параллельно одной
из диагоналей проекций квадратов,
лежащих в соответствующих координатных
плоскостях, стороны которых параллельны
аксонометрическим осям ( ГОСТ 2.31769,
СТ СЭВ 197979).
На рис. 7 показано направление штриховки
в диметрии.
9
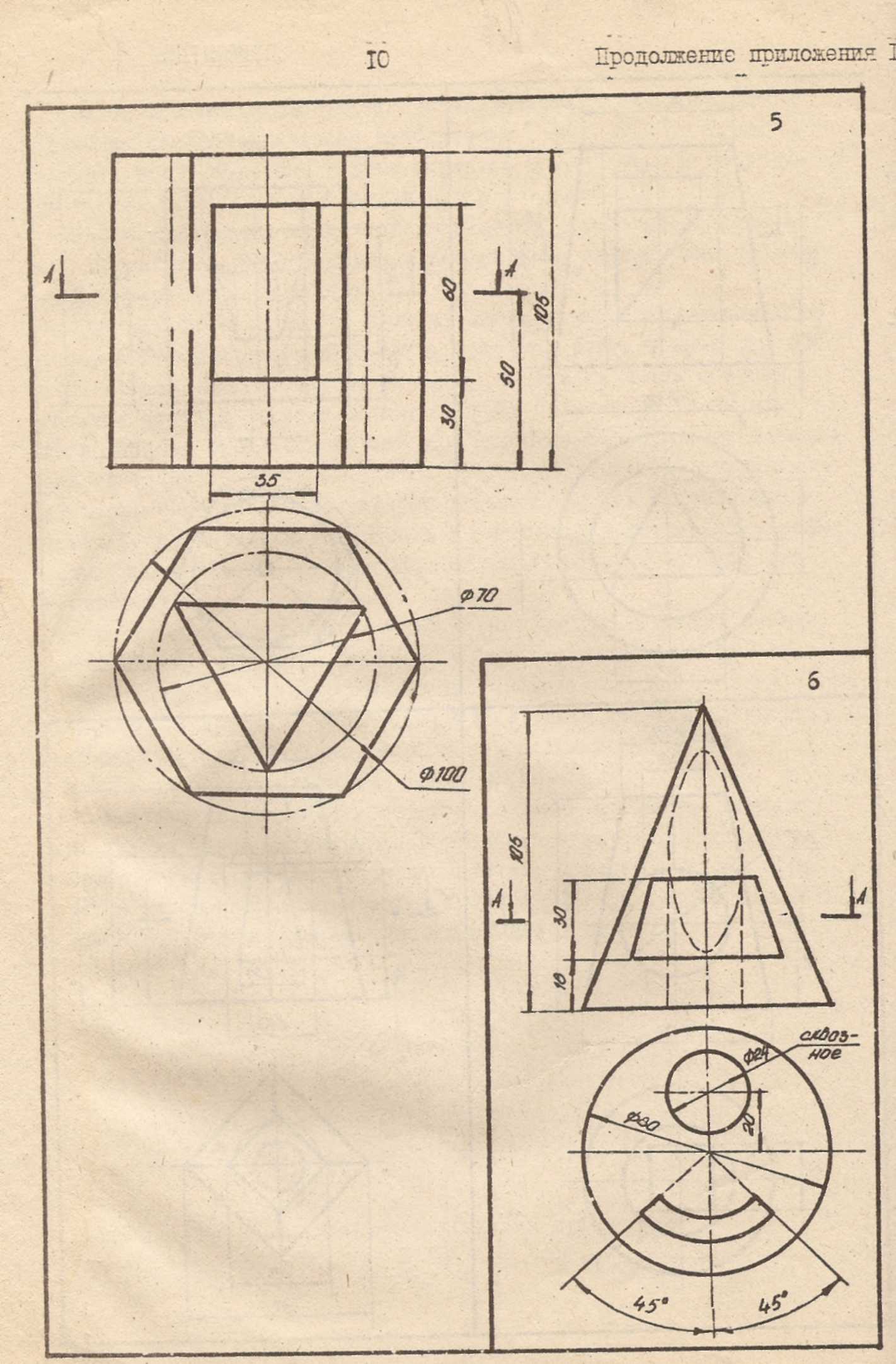
ПРИЛОЖЕНИЕ 1

10
Продолжение приложения 1
11
Продолжение приложения 1

12
Продолжение приложения 1

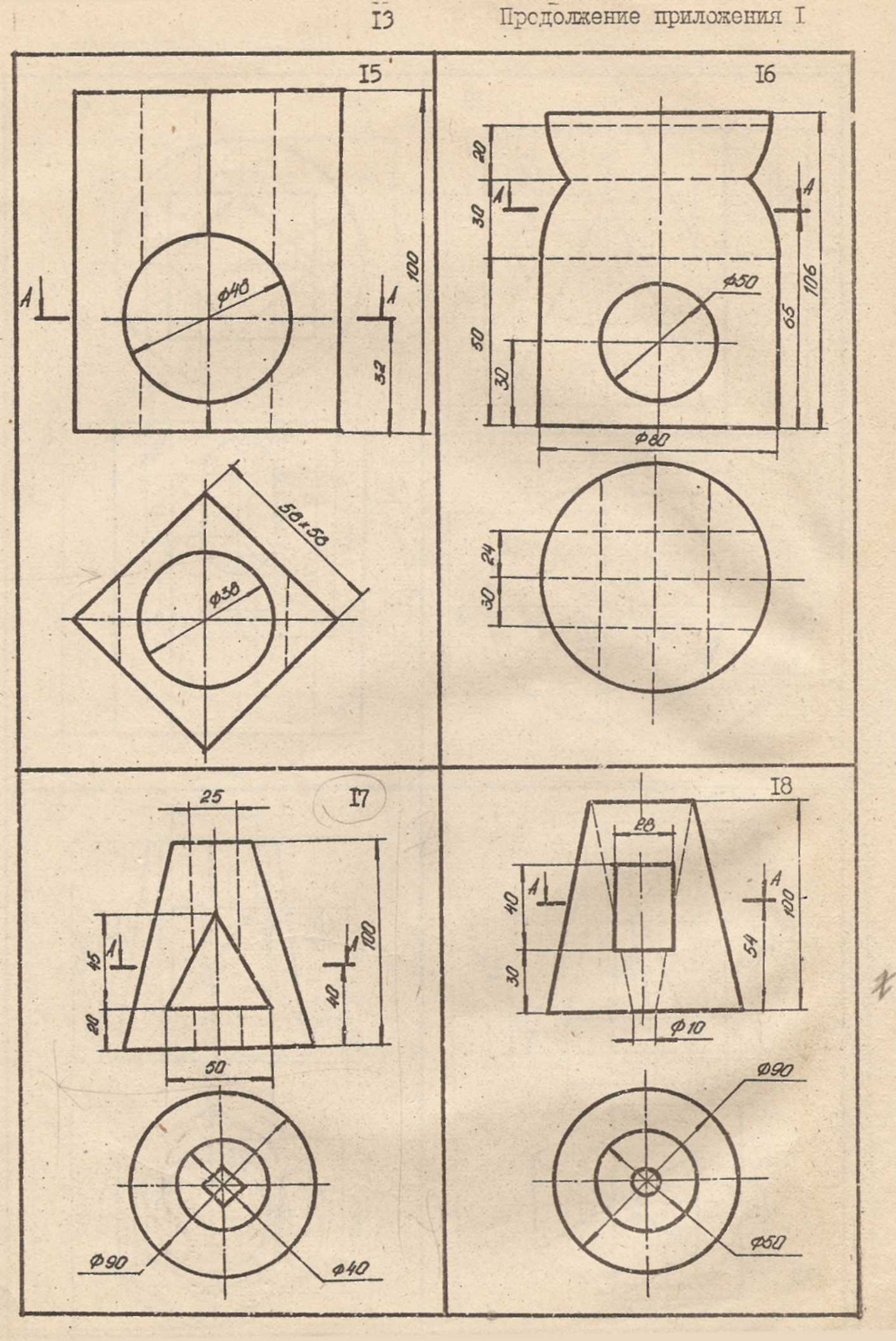
13
Продолжение приложения 1


Продолжение приложения 1

Продолжение приложения 1

Продолжение приложения 1

Продолжение приложения 1

Продолжение приложения 1
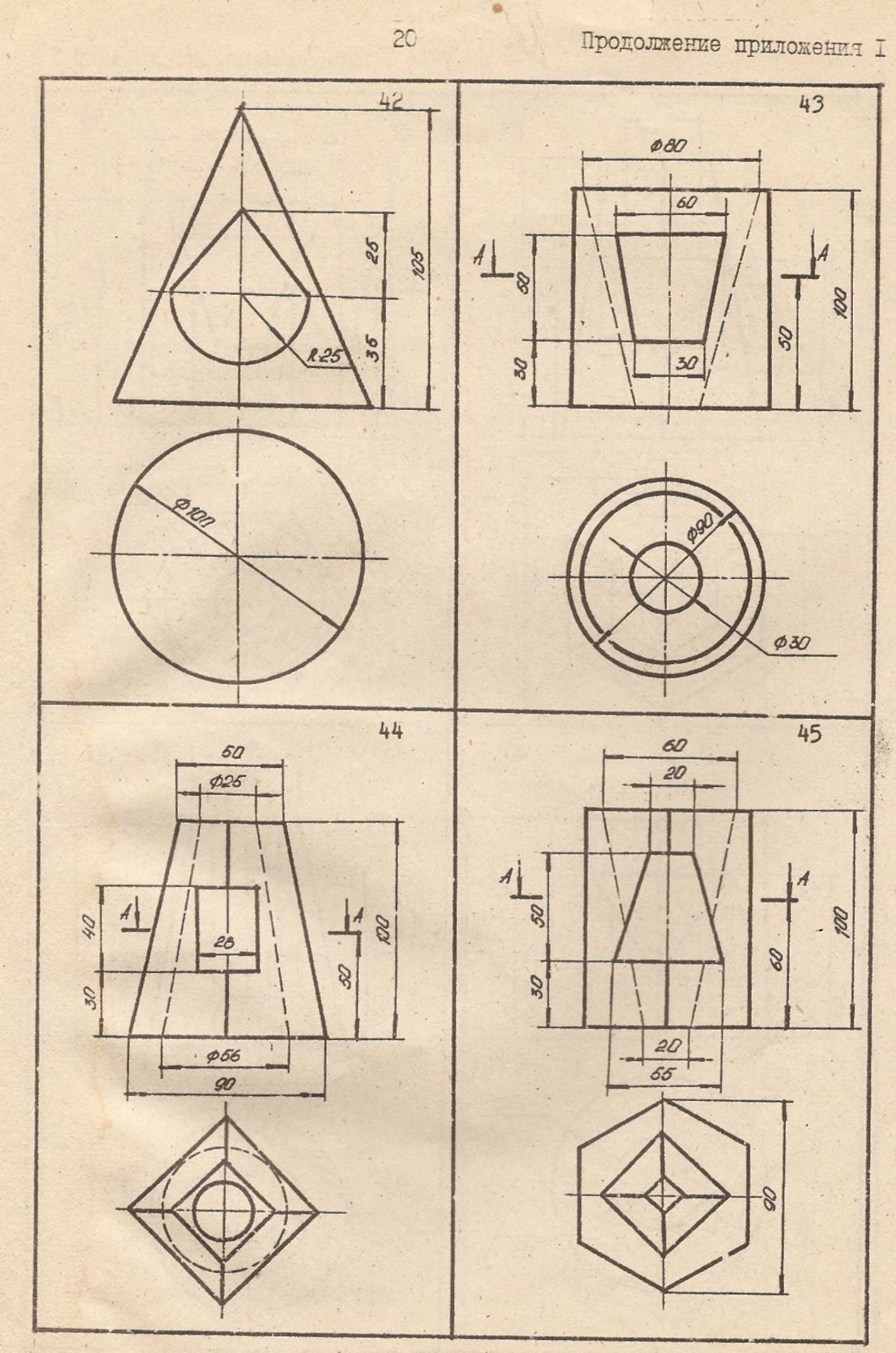
Продолжение приложения 1
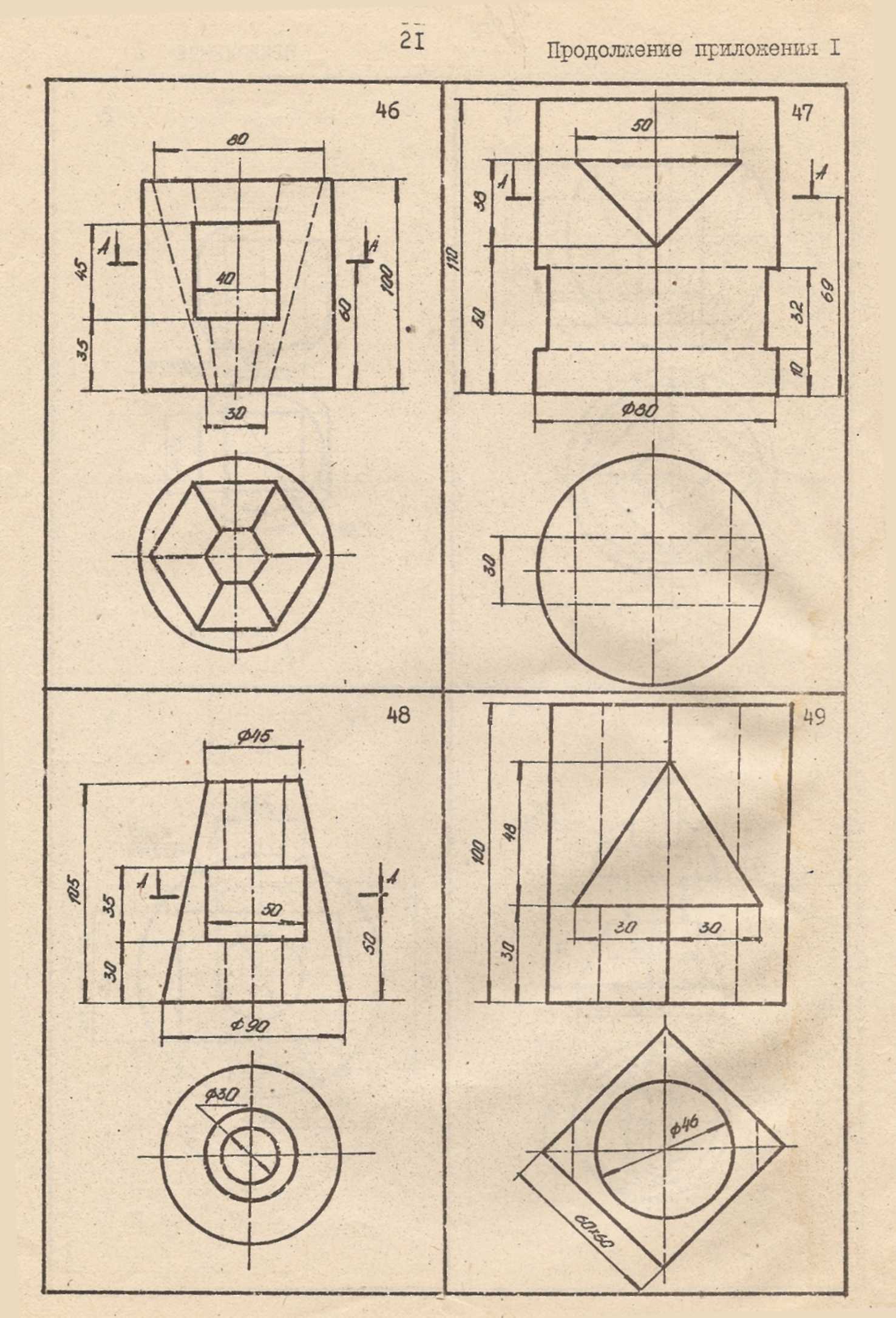
ПРИЛОЖЕНИЕ 2
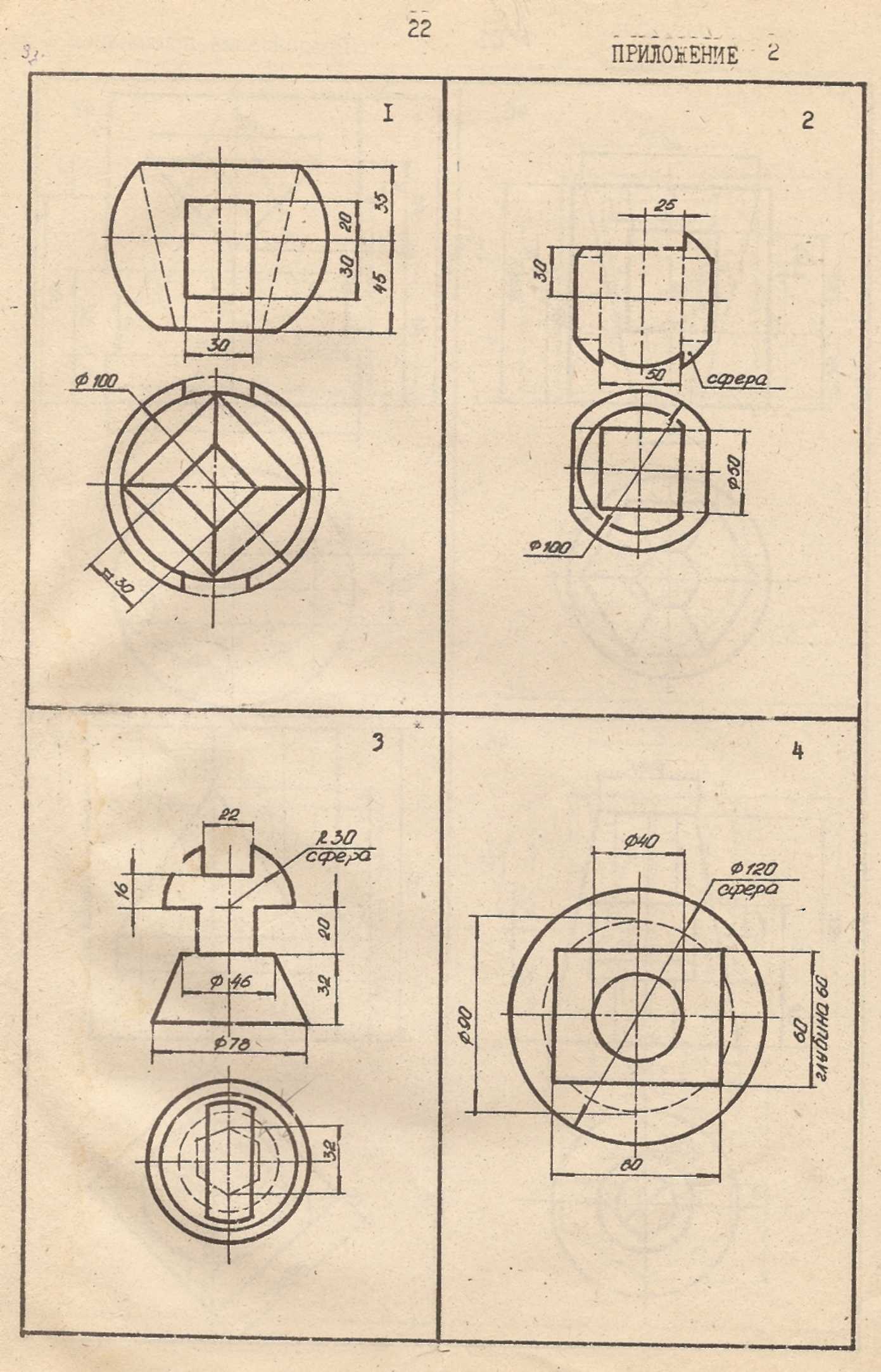
Продолжение приложения 2

Продолжение приложения 2
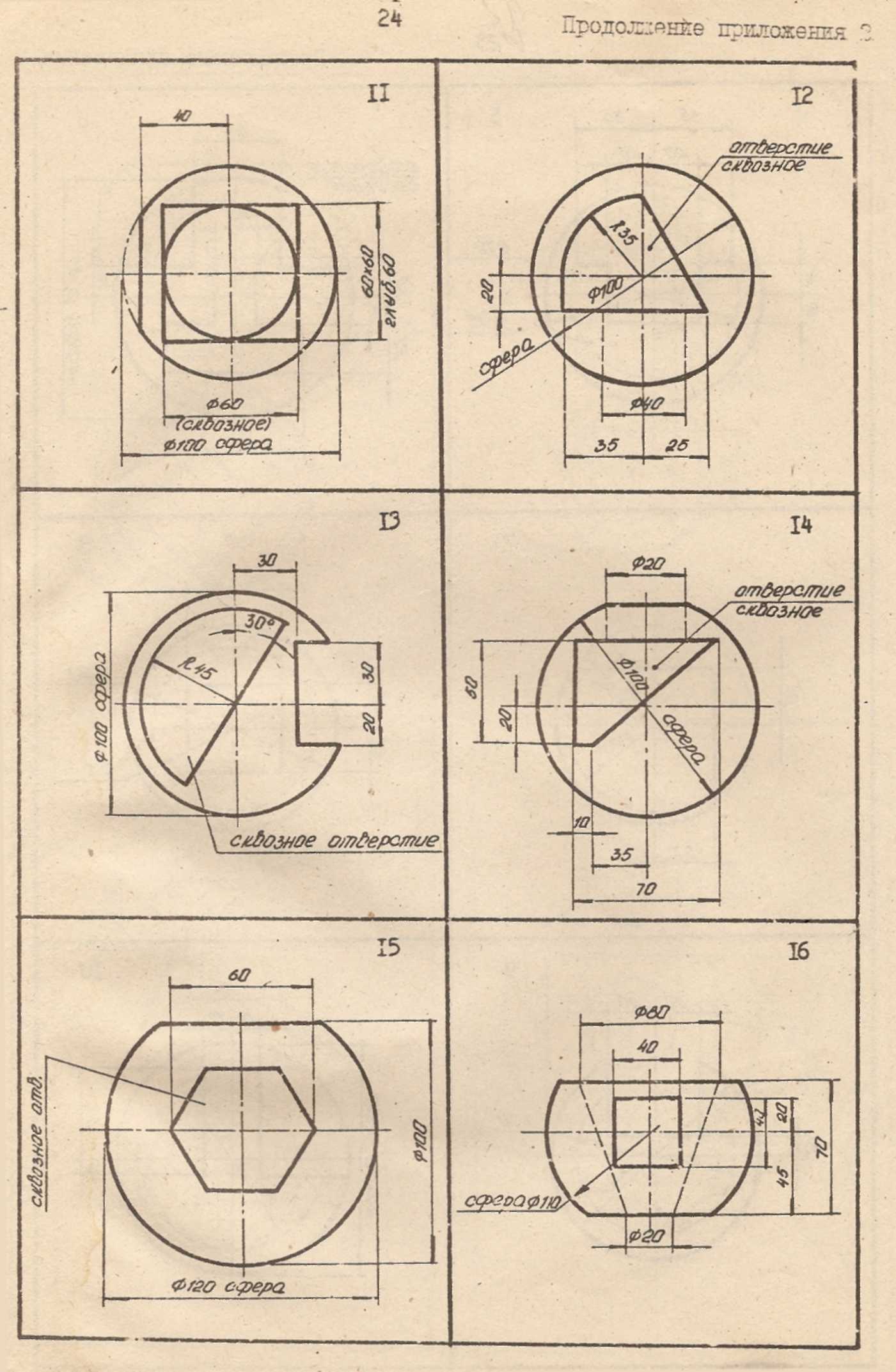
Продолжение приложения 2

Продолжение приложения 2

Продолжение приложения 2


Продолжение приложения 2

Продолжение приложения 2
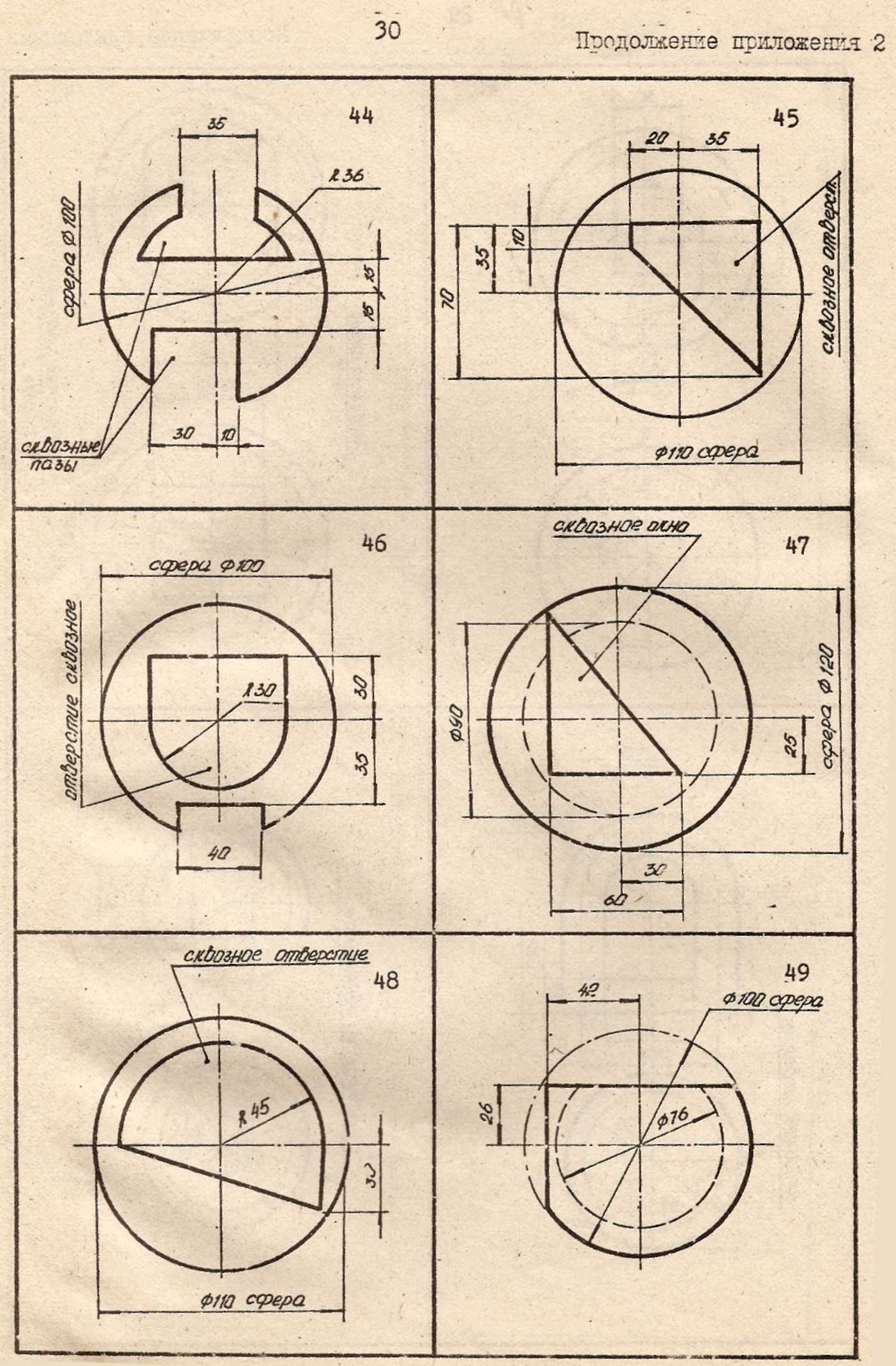
СПИСОК ЛИТЕРАТУРЫ:
Основная литература:
1. Нартова Л.Г. Начертательная геометрия: Учеб. М.: Академия, 2011.
2. Гордон В.О. Начертательная геометрия. – М.: Высш. шк., 2002.
3. Гордон В.О. Сборник задач по курсу начертательной геометрии. – М.: Высш. шк., 2003.
Дополнительная литература:
1. Чекмарев А.А. Начертательная геометрия и черчение: Учеб. М.: Юрайт, 2011.
2. Стрижаков А.В. и др. Начертательная геометрия: Учеб. пос. для вузов. Ростов н/Д: Феникс, 2004.
СОДЕРЖАНИЕ
