
Приклади розв’язання задач.
Задача 1. Знайти відстань між
діагоналями
![]() та
та
![]() граней куба
граней куба
![]() ,
ребро якого дорівнює 1. Які точки вказаних
діагоналей знаходяться на знайденій
відстані?
,
ребро якого дорівнює 1. Які точки вказаних
діагоналей знаходяться на знайденій
відстані?
Р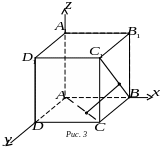 озв’язання.
Нехай
заданий куб. Виберемо систему координат
у виді репера
озв’язання.
Нехай
заданий куб. Виберемо систему координат
у виді репера
![]() (рис. 3). Очевидно, що кінці заданих
діагоналей мають координати
(рис. 3). Очевидно, що кінці заданих
діагоналей мають координати
![]() ,
,
![]() ,
,
![]() ,
,
![]() і
і
![]() ,
,
![]() .
Складемо рівняння площини
,
яка проходить через діагональ
паралельно до прямої
.
Дістаємо
.
Складемо рівняння площини
,
яка проходить через діагональ
паралельно до прямої
.
Дістаємо
![]() :
:
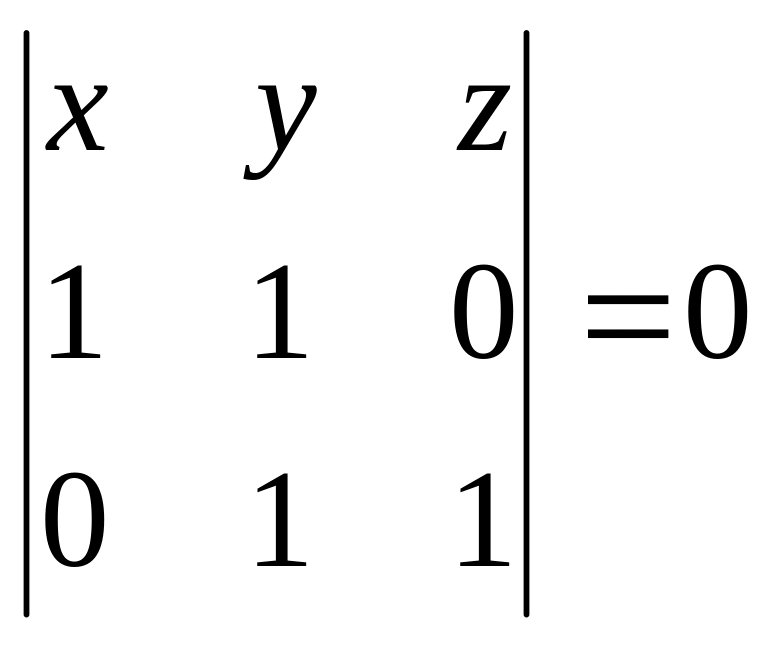 або
або
![]() .
.
Відстань
![]() між діагоналями куба тепер можна знайти
за допомогою співвідношення (6):
між діагоналями куба тепер можна знайти
за допомогою співвідношення (6):
![]() .
.
Щоб дати відповідь на другу частину
задачі, складемо рівняння двох площин
та
,
які проходять перпендикулярно до
та містять діагоналі
та
.
При цьому використовуємо перпендикулярний
до
вектор
![]() .
Маємо
.
Маємо
![]() :
:
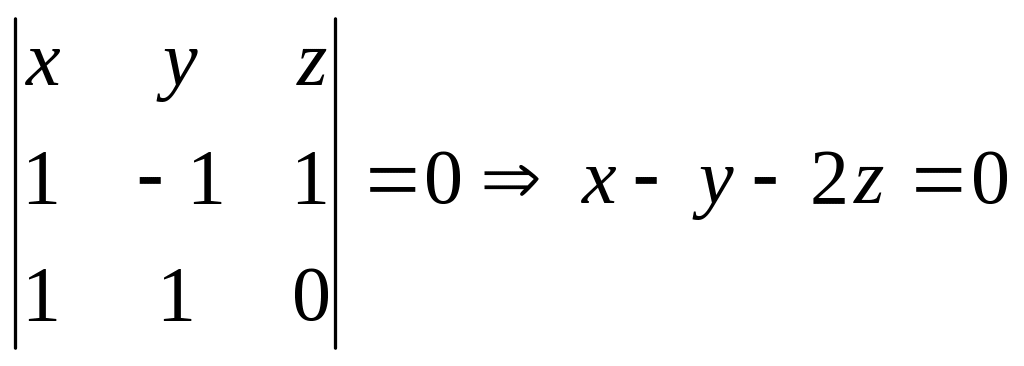 ,
,
![]() :
:
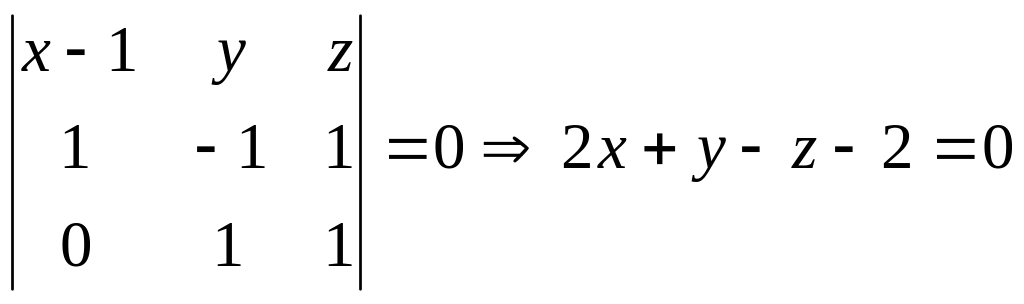 .
.
Система рівнянь
![]() визначає спільний перпендикуляр до
прямих
та
.
Він перетинає діагональ
у точці, для якої
.
Використавши цей факт, знаходимо
визначає спільний перпендикуляр до
прямих
та
.
Він перетинає діагональ
у точці, для якої
.
Використавши цей факт, знаходимо
![]() .
Ця ж пряма перетинає діагональ
у точці з абсцисою
.
Ця ж пряма перетинає діагональ
у точці з абсцисою
![]() Звідси
Звідси
![]() .
Можна переконатися, що відстань між
одержаними точками дорівнює
.
Можна переконатися, що відстань між
одержаними точками дорівнює
![]() .
.
Задача 2. Як розташовані в
просторі прямі
![]() та
та
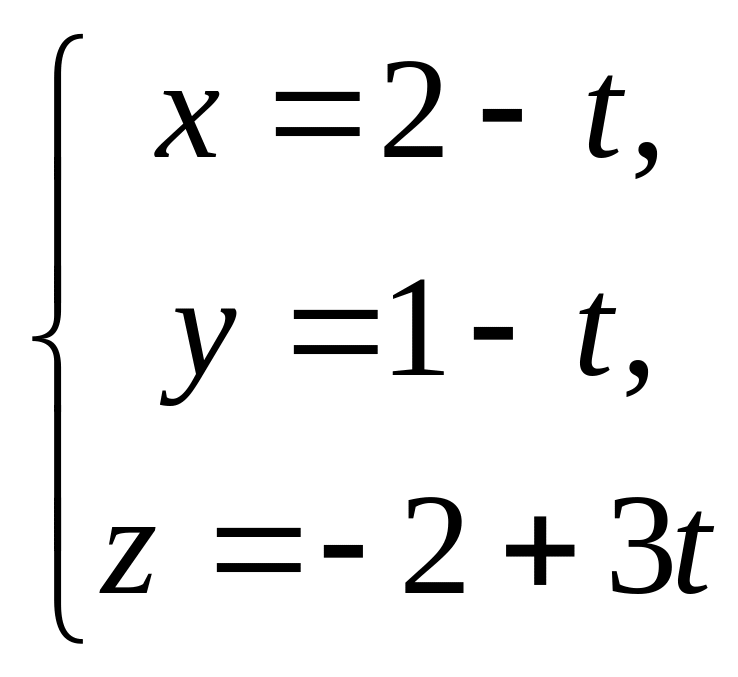 ?
?
Розв’язання. Знайдемо два
довільні розв’язки системи, яка задає
першу пряму. Нехай вони визначають точки
![]() та
та
![]() .
Друга пряма задається точкою
.
Друга пряма задається точкою
![]() та напрямним вектором
та напрямним вектором
![]() .
Обчислимо мішаний добуток векторів
.
Обчислимо мішаний добуток векторів
![]() ,
,
![]() та
та
![]() .
.
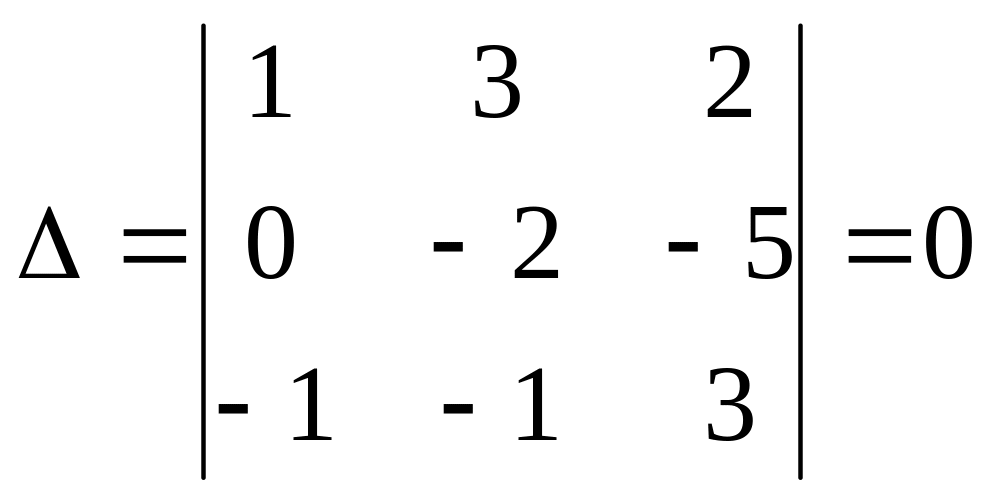 .
.
Отже, прямі лежать в одній площині.
Оскільки їхні напрямні вектори (![]() та
)
не колінеарні, то прямі перетинаються.
та
)
не колінеарні, то прямі перетинаються.
Задача 3. Знайти відстань між
прямими
![]() та
та
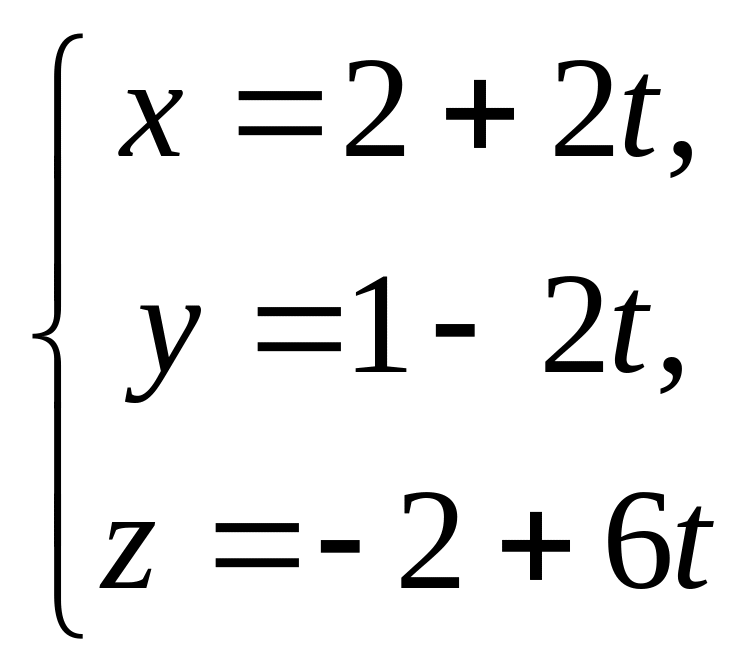 .
.
Розв’язання. Перший спосіб.
Очевидно, що задані прямі паралельні,
оскільки їхні напрямні вектори
![]() та
та
![]() колінеарні. Першій прямій належить
точка
колінеарні. Першій прямій належить
точка
![]() ,
а другій – точка
,
а другій – точка
![]() .
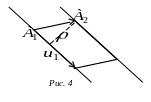
Відстань
між прямими знайдемо як висоту
паралелограма, побудованого на векторах
та
.
Відстань
між прямими знайдемо як висоту
паралелограма, побудованого на векторах
та
![]() ,
яка проведена до сторони, паралельної
до
(рис. 4). Площу паралелограма знайдемо
за допомогою векторного добутку:
,
яка проведена до сторони, паралельної
до
(рис. 4). Площу паралелограма знайдемо
за допомогою векторного добутку:
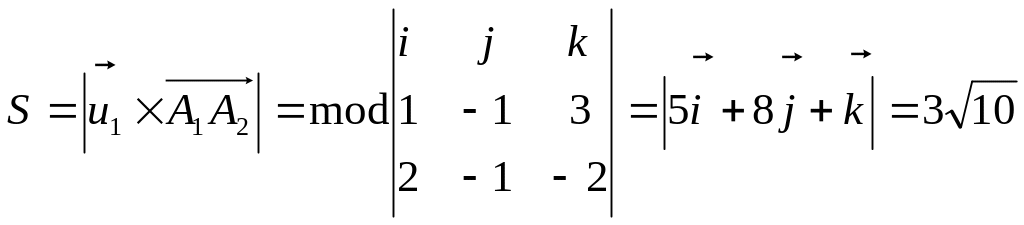
 .
.
Оскільки
![]() ,
то
,
то
![]() .
.
Другий спосіб. Через точку
![]() проведемо площину, перпендикулярну до
заданих прямих. ЇЇ рівняння запишеться
у виді
проведемо площину, перпендикулярну до
заданих прямих. ЇЇ рівняння запишеться
у виді
![]() або
або
![]() .
Знайдемо точку перетину цієї площини
з другою прямою. Із системи
.
Знайдемо точку перетину цієї площини
з другою прямою. Із системи
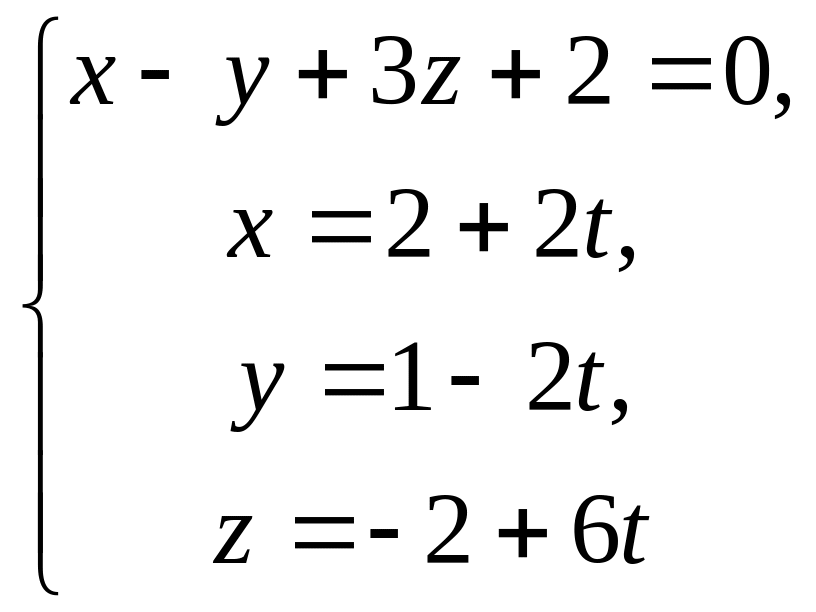 дістаємо
дістаємо
![]() .
Відстань від знайденої точки до точки
буде шуканою. Дістаємо
.
Відстань від знайденої точки до точки
буде шуканою. Дістаємо
![]() .
.
З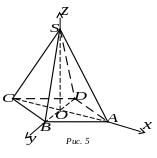 адача
4. В основі чотирикутної піраміди
лежить ромб із діагоналями 6 та 8. Висота
піраміди дорівнює 5. Знайти відстань
між мимобіжними більшим бічним ребром
та стороною основи.
адача
4. В основі чотирикутної піраміди
лежить ромб із діагоналями 6 та 8. Висота
піраміди дорівнює 5. Знайти відстань
між мимобіжними більшим бічним ребром
та стороною основи.
Розв’язання. Нехай
- задана піраміда. Будемо шукати
відстань між ребрами
![]() та
.
Виберемо систему координат так, як
зображено на рисунку 3. Згідно з умовою
задачі, отримуємо
та
.
Виберемо систему координат так, як
зображено на рисунку 3. Згідно з умовою
задачі, отримуємо
![]() ,
,
![]() ,
,
![]() ,
,
![]() і
і
![]() ,
,
![]() .
Складемо рівняння площини
,
яка проходить через ребро
.
Складемо рівняння площини
,
яка проходить через ребро
![]() паралельно до прямої
паралельно до прямої
![]() .
Дістаємо
.
Дістаємо
:
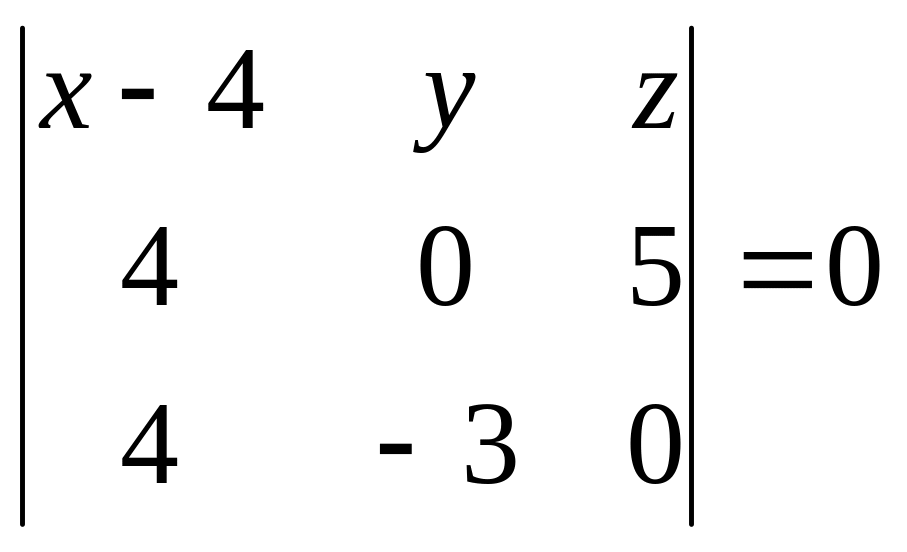
або
![]() .
.
Відповідь на задачу отримуємо, знайшовши відстань від точки до площини :
![]() .
.
Задача 5. Скласти рівняння
прямої, яка проходить через точку
![]() та перетинає прямі
та перетинає прямі
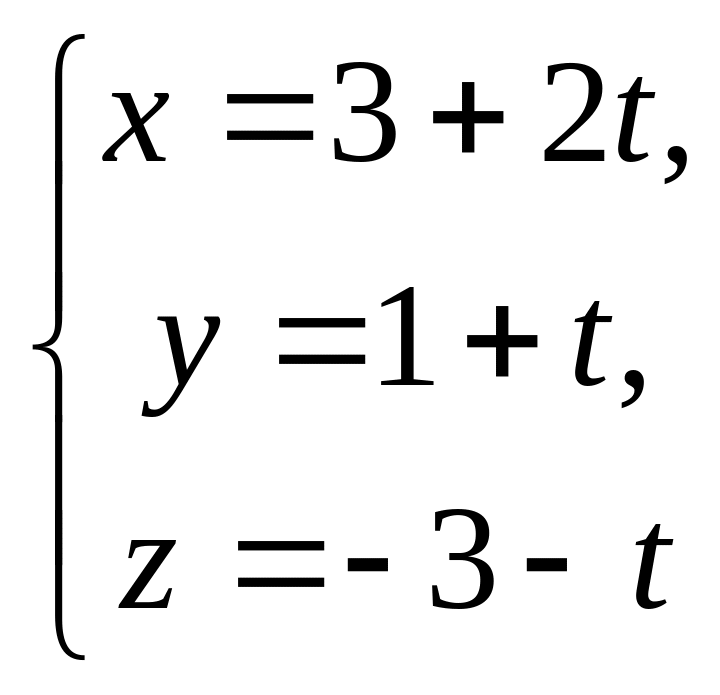 ,
,
![]() .
.
Розв’язання. Візьмемо на
першій прямій точку
![]() та на другій прямій – точку
та на другій прямій – точку
![]() ,
положення яких змінюється при зміні
параметрів
,
положення яких змінюється при зміні
параметрів
![]() та
та
![]() .
Підберемо ці параметри так, щоб точки
.
Підберемо ці параметри так, щоб точки
![]() належали одній прямій. Із колінеарності
векторів
належали одній прямій. Із колінеарності
векторів
![]() ,
,
![]() отримуємо рівності
отримуємо рівності
![]() ,
,
звідки, ввівши заміну
![]() ,
дістаємо систему лінійних рівнянь
,
дістаємо систему лінійних рівнянь
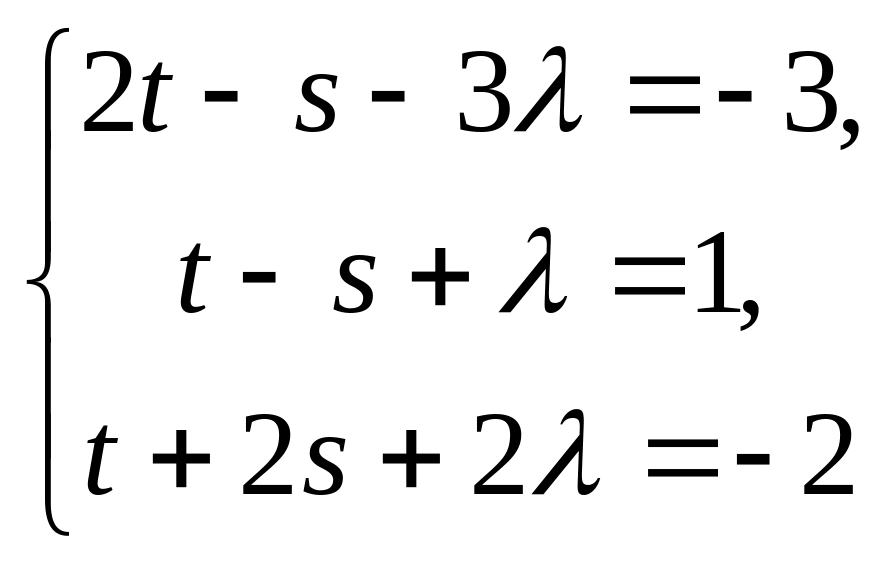 .
.
Додаючи до першого рівняння системи
два інші, дістаємо
![]() .
Це дозволяє
знайти точку
.
Це дозволяє
знайти точку
![]() та записати відповідь у вигляді рівняння
прямої, що проходить через точку
у напрямку вектора
та записати відповідь у вигляді рівняння
прямої, що проходить через точку
у напрямку вектора
![]() .
.
Відповідь.
![]() .
.
Задача 6. Знайти точку, яка симетрична до точки відносно прямої .
Розв’язання. Знайдемо
рівняння прямої, яка проходить через
точку
та перетинає задану пряму під прямим
кутом. Запишемо її рівняння у виді
![]() (ми вибираємо напрямний вектор прямої
з першою координатою 1, передбачаючи
перспективу розгляду випадку, коли вона
дорівнює 0). Позначимо через
(ми вибираємо напрямний вектор прямої
з першою координатою 1, передбачаючи
перспективу розгляду випадку, коли вона
дорівнює 0). Позначимо через
![]() точку на заданій прямій. Умову перетину
прямих запишемо у виді рівності 0 мішаного
добутку векторів
точку на заданій прямій. Умову перетину
прямих запишемо у виді рівності 0 мішаного
добутку векторів
![]() ,
,
![]() та
та
![]() .
Дістаємо
.
Дістаємо
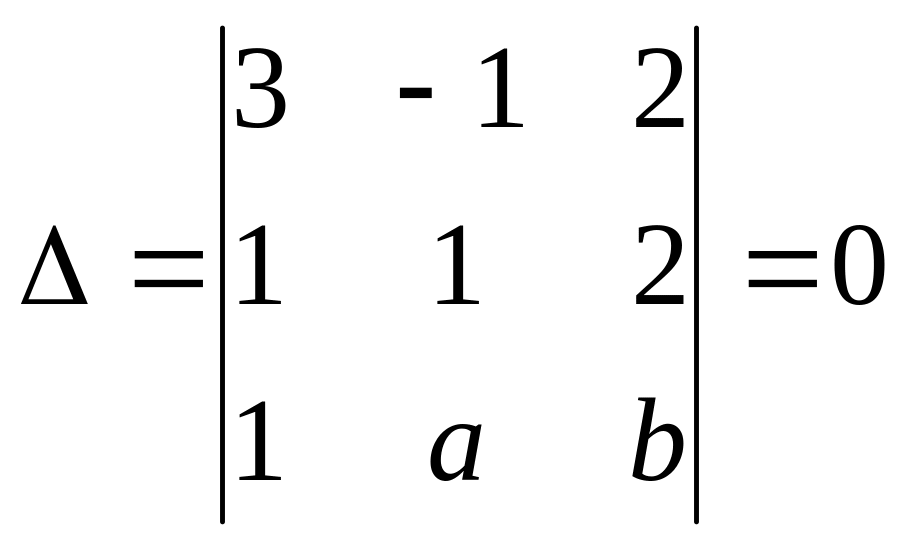 .
Звідси
.
Звідси
![]() .
Умова перпендикулярності прямих,
записана у виді
.
Умова перпендикулярності прямих,
записана у виді
![]() ,
дозволяє отримати співвідношення
,
дозволяє отримати співвідношення
![]() .
Із системи рівнянь
.
Із системи рівнянь
![]() знаходимо
знаходимо
![]() .
.
Запишемо рівняння знайденої прямої у
параметричному виді
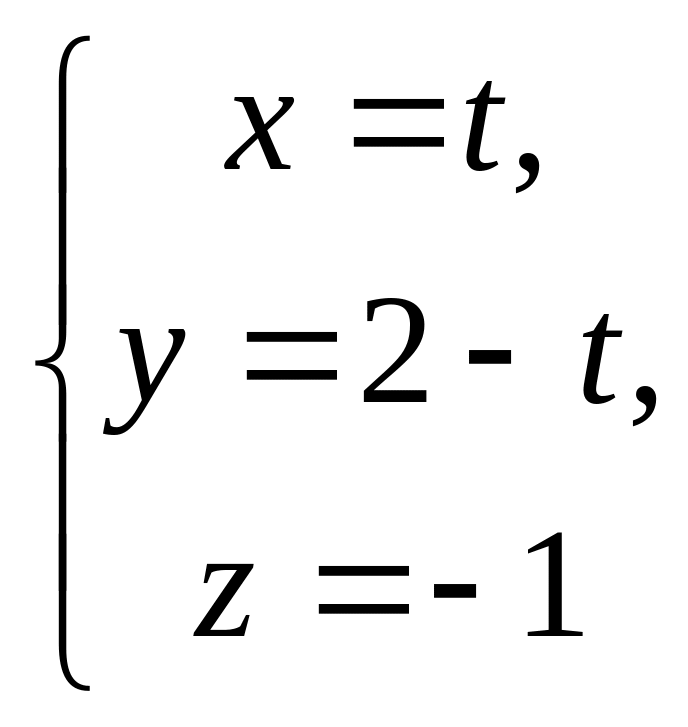 та знайдемо точку, в якій вона перетинає
задану пряму. Із системи
та знайдемо точку, в якій вона перетинає
задану пряму. Із системи
![]() дістаємо
дістаємо
![]() та шукану точку перетину
та шукану точку перетину
![]() .
Для відшукання точки
.
Для відшукання точки
![]() ,
яка симетрична до точки
відносно точки
,
яка симетрична до точки
відносно точки
![]() ,
отримуємо співвідношення
,
отримуємо співвідношення
![]() ,
звідки
,
звідки
![]() .
.
Відповідь.
![]() .
.
