Основні теоретичні факти.

Якщо пряма задана точкою та напрямним вектором , то її рівняння записують у виді

. (1)

Його називають канонічним рівнянням прямої в просторі.

Прирівнявши одержані відношення до параметра , дістаємо співвідношення

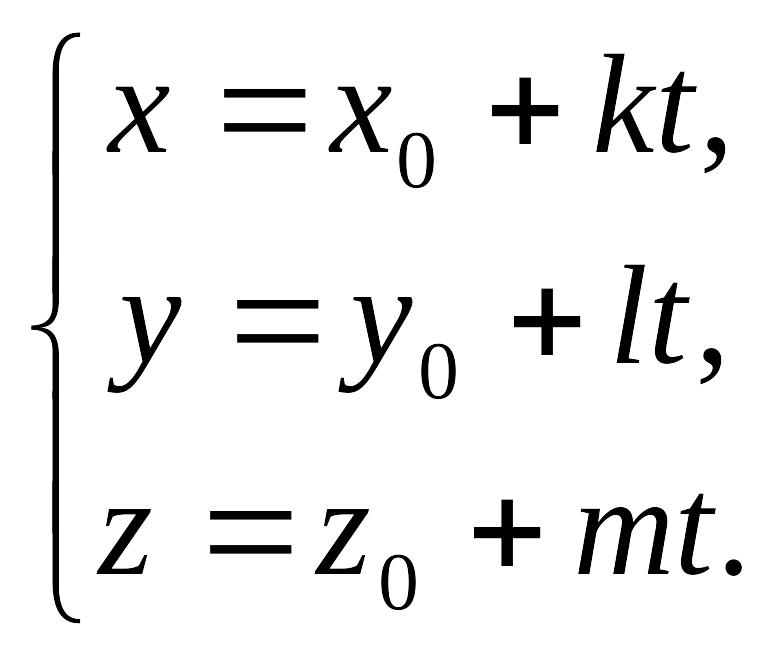(2)

Одержані рівняння називають параметричними рівняннями прямої в просторі. Їх використовують, наприклад, у випадку, коли деякі з чисел у рівнянні (1) рівні нулю. Зауважимо, що у деякій літературі зустрічаються записи, коли у одному або двох знаменниках рівняння виду (1) наявні нулі. Його потрібно сприймати символічно, розуміючи наявність нульових координат у напрямного вектора.

Нехай пряма проходить через дві точки . Тоді її рівняння можна записати у виді

(3)

Одержане співвідношення називають рівнянням прямої в просторі, що проходить через дві задані точки.

У деяких випадках пряму в просторі зручно задавати, як лінію перетину двох площин, тобто у виді системи рівнянь

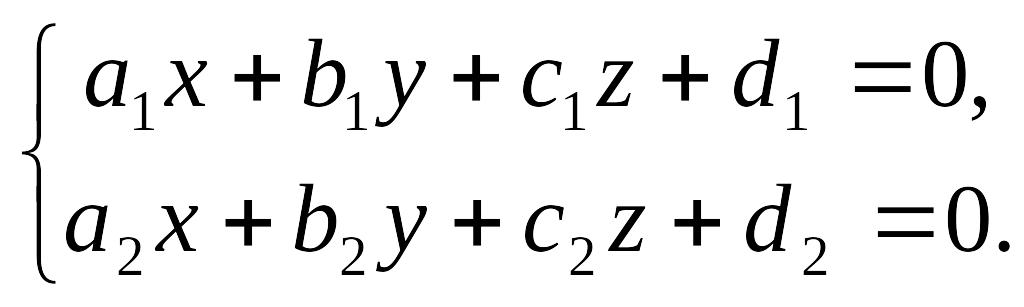(4)

Перехід від задання прямої у виді (4) до виду (1) чи (2) можна здійснювати, знайшовши два довільні розв’язки системи (4), або знайшовши координати напрямного вектора прямої, який можна одержати, як векторний добуток векторів нормалей та до даних площин. Перехід від задання прямої у виді (1) чи (2) до виду (4) очевидний.

Розглянемо в просторі дві прямі та , кожна з яких задається точкою , що належить прямій, та напрямним вектором , .

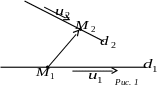
Очевидно, що випадки, коли обидві прямі лежать в одній площині (тобто паралельні або перетинаються ), чи мимобіжні, залежать від того, чи компланарні вектори , та (рис. 1). Оскільки необхідною та достатньою умовою компланарності трьох векторів є рівність нулю їхнього мішаного добутку, то розташування прямих залежить від числа

.

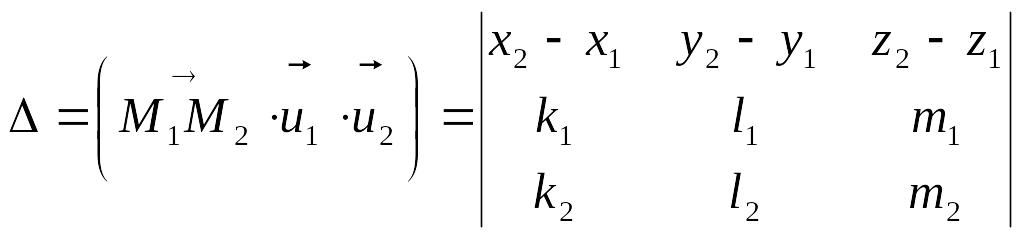
Якщо , то вектори , та компланарні, тому прямі та лежать в одній площині. Якщо при цьому вектори та колінеарні, тобто виконуються умови

, (5)

то .

Якщо і умова (5) не виконується, то прямі та перетинаються. Прямі та можуть співпадати, якщо крім умови (5) виконується також рівність

яка означає, що точка одночасно належить також першій прямій.

Якщо , то вектори , та не компланарні, а прямі та мимобіжні.

Кутом між двома мимобіжними прямими в просторі називають кут між двома прямими, які проходять через деяку спільну точку і паралельні до заданих прямих. У випадку аналітичного задання прямих та кут між ними шукають як кут між їхніми напрямними векторами та

.

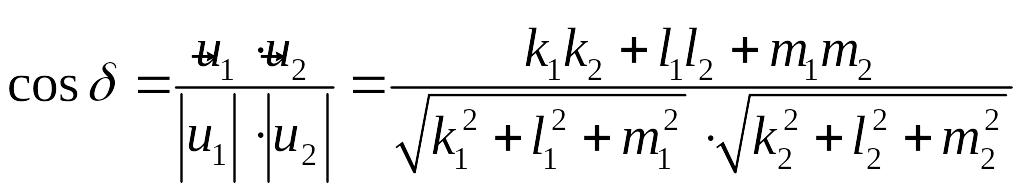Нехай дві мимобіжні прямі задані своїми канонічними рівняннями

: .

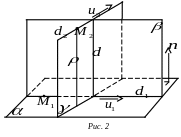
Пряма, яка перетинає задані прямі та перпендикулярна до них, називається спільним перпендикуляром до цих прямих.

Існування та єдиність спільного перпендикуляра обґрунтовується в шкільному курсі геометрії. Для побудови спільного перпендикуляра до прямих та через пряму проводять площину , яка паралельна до прямої . Для цього використовується точка та вектори , які паралельні до . Аналітично рівняння площини запишеться у виді рівності

.

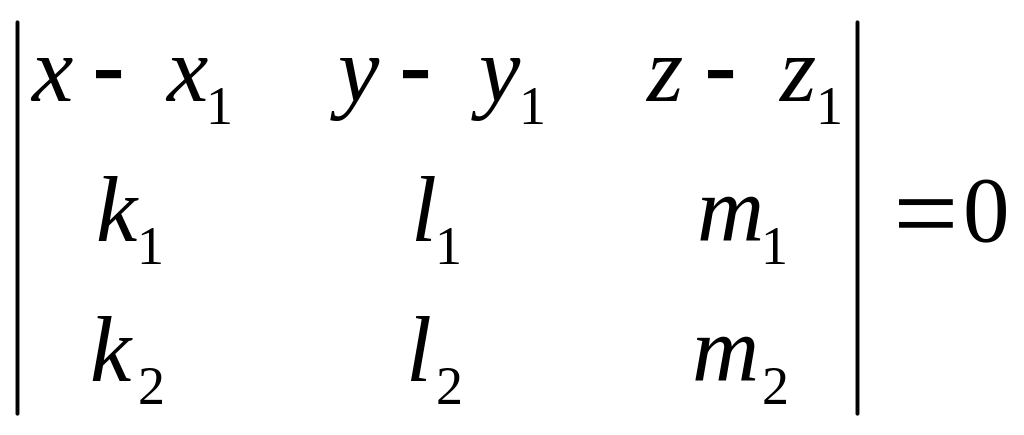Нехай після необхідних обчислень таке рівняння набуде виду .

Позначимо через вектор, який перпендикулярний до площини . Проведемо дві площини та , кожна з яких перпендикулярна до площини та проходить через прямі та відповідно. При цьому площина визначається точкою та паралельними до неї векторами та , а площина - точкою та паралельними до неї векторами та .

Рівняння площин та можна записати у виді рівностей

,

.

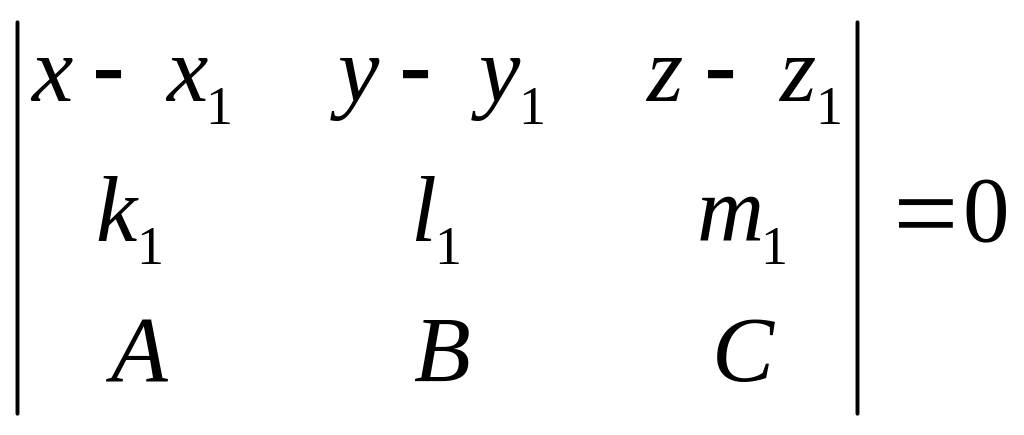
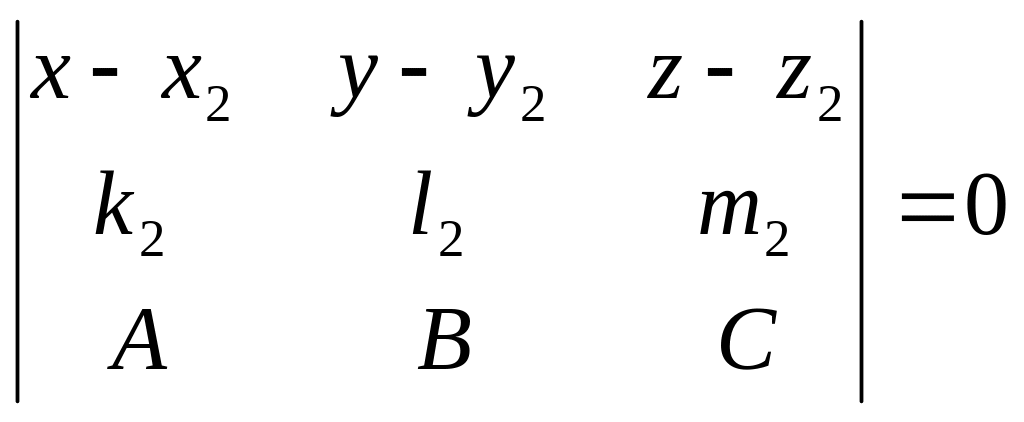Пряма , по якій перетинаються площини та , буде шуканим спільним перпендикуляром до прямих та (рис. 2). Рівняння спільного перпендикуляра до прямих та можна записати у вигляді системи рівнянь, які задають площини та .

Відстань між мимобіжними прямими та можна знайти, як відстань від точки до площини , тобто

. (6)