73

Практичне заняття №10. Різні способи задання площини.

Відстань від точки до площини. Геометричний зміст знаку виразу . Дві площини в просторі.

Основні теоретичні факти.

Н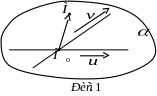 ехай у в довільній афінній системі координат площина задається перетином двох прямих. Нехай - спільна точка цих прямих, а не колінеарні вектори та задають напрямки прямих (рис. 1). Тоді рівняння площини записується у виді

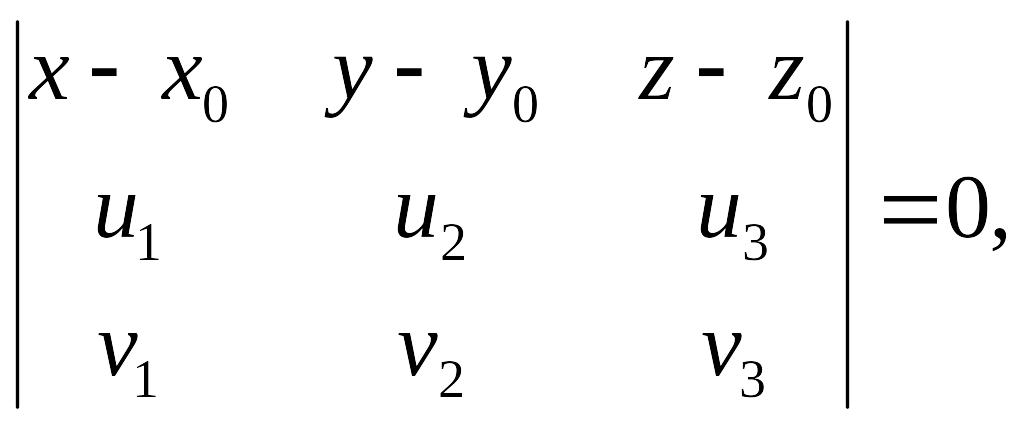(1)

або

, (2)

де 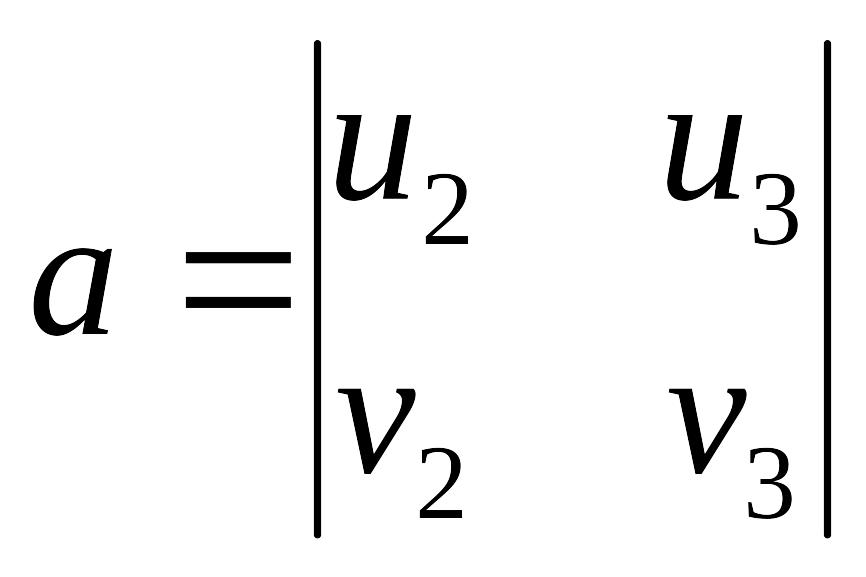, , 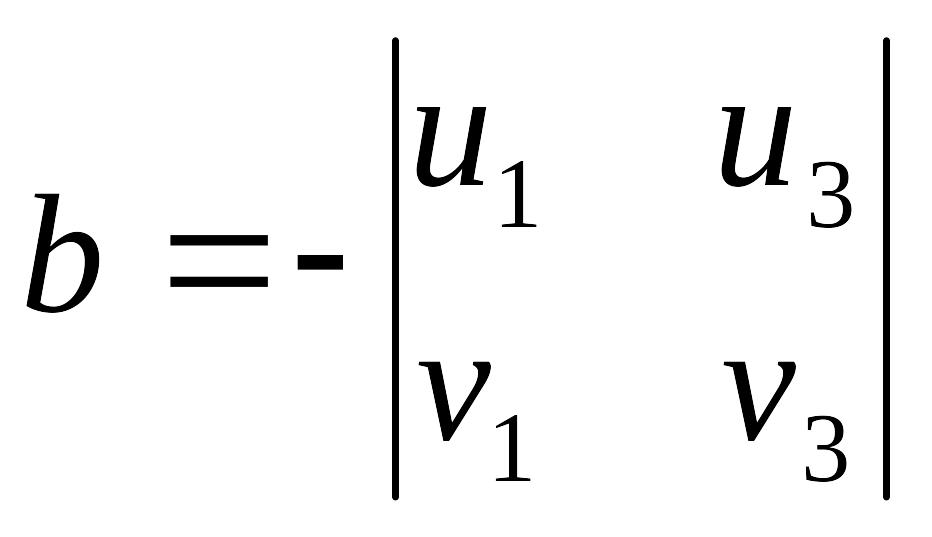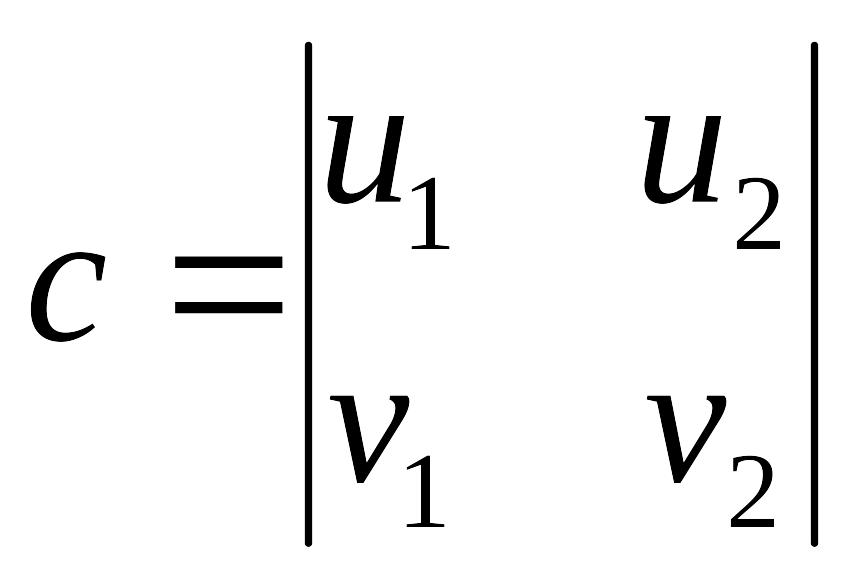.Дані числові коефіцієнти одночасно не дорівнюють нулю.

Н ехай площина задана трьома точками , які не лежать на одній прямій. Тоді рівняння площини матиме вид

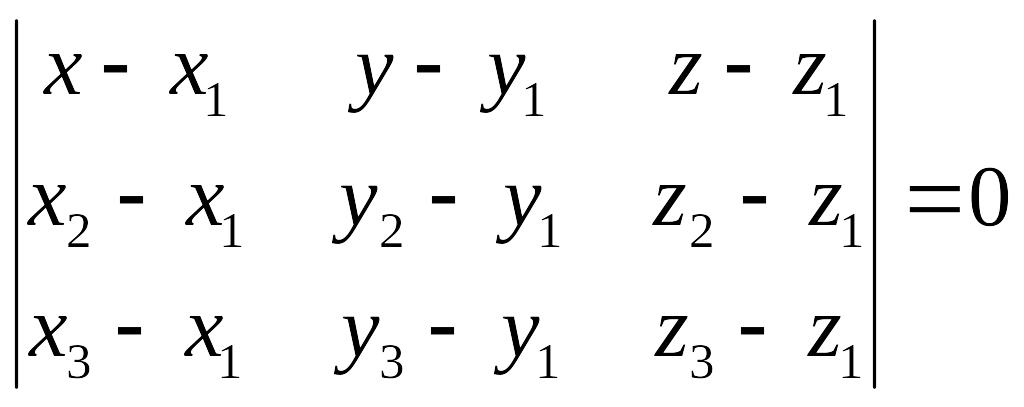. (3)

Його називають рівнянням площини, що проходить через три задані точки.

Нехай площина відтинає на осях відрізки відповідно (рис.2). Рівняння площини у цьому випадку записується у виді

(4)

Його називають рівнянням площини у відрізках на осях.

Н ехай задана прямокутна декартова система координат . Розглянемо деяку площину із заданою на ній точкою та вектором який перпендикулярний до площини (рис.3). Рівняння

. (5)

є рівнянням площини, яка проходить через задану точку, перпендикулярно до заданого напрямку.

Рівняння (2), до якого зводяться рівняння площини в усіх розглянутих випадках, називають загальним рівнянням площини. У прямокутній декартовій системі координат коефіцієнти біля змінних та визначають вектор , який перпендикулярний до площини.

Для того, щоб вектор був паралельним до площини , заданої рівнянням , необхідно та достатньо, щоб виконувалася рівність

. (6)

Частинні випадки рівняння (1):

1. При площина проходить через початок координат.

2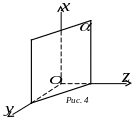 . При тобто у випадку, коли рівняння має вид , площина проходить паралельно до осі (рис. 4). Аналогічні висновки робимо при та . Тобто площина, задана рівнянням паралельна до осі , а площина, задана рівнянням , паралельна до осі . Якщо або , то площина проходить через вісь (відповідно через вісь або вісь ).

3

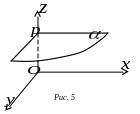
. У випадку, коли , рівняння площини набуває виду або , де . Тоді площина буде паралельною до площини (рис. 5). При рівняння є рівнянням площини . Аналогічно, якщо , то рівняння задає площину, яка паралельна до площини ( ). Рівняння та є рівняннями відповідно площин та .

Нехай у прямокутній декартовій системі координат рівняння ax+by+cz+d=0 визначає деяку площину , а також задана точка . Відстань від даної точки до площини обчислюється за допомогою співвідношення

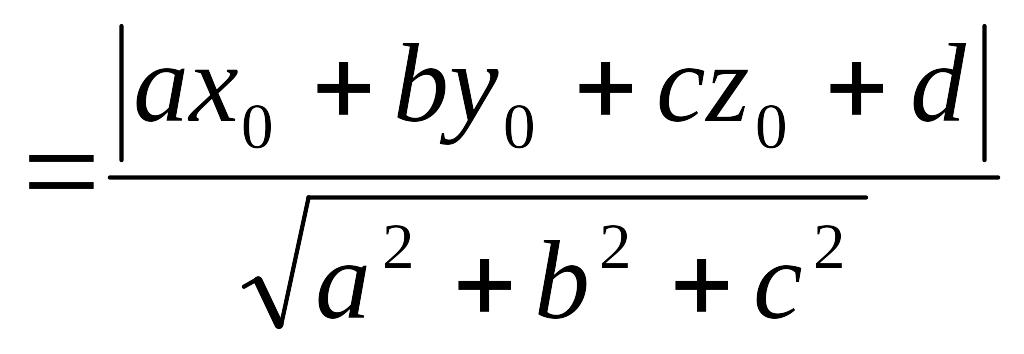. (7)

Площина розбиває весь простір на два півпростори. Нерівності >0 та <0 аналітично задають множини точок цих півпросторів.

Нехай у деякій афінній системі координат рівняння , задають дві площини та . При виконанні умови

(8)

вони будуть паралельними. Якщо виконуються пропорції

,

то площини співпадають. Нехай умова (8) паралельності площин не виконується, тобто вони перетинаються. При перетині утворюються чотири двогранні кути (рис. 3). Вважаючи систему координат прямокутною декартовою, кут між площинами можна обчислити за допомогою співвідношення

.

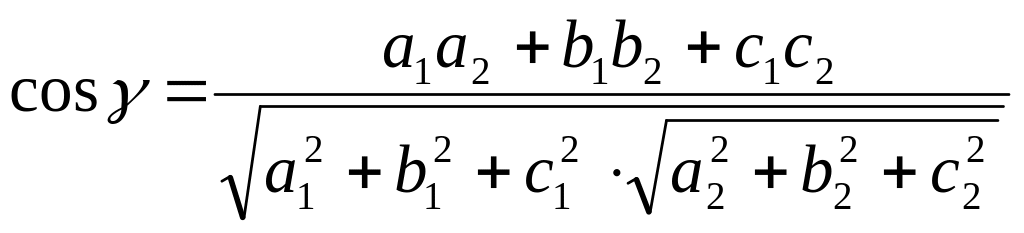Зокрема площини будуть перпендикулярними тоді і тільки тоді, коли виконується умова

.

У випадку паралельності площин та їхні рівняння можна записати у виді

, .

Відстань між ними обчислюють за допомогою співвідношення

.