3. Зависимость скорости реакции от температуры

Повышение температуры ускоряет большинство химических реакций. Согласно правилу Вант-Гоффа при повышении температуры на каждые 10⁰С скорость реакций увеличивается в 2-4 раза.

(5)

₂ и ₁ – скорости реакций, соответствующих температуре t₂ и t₁,

где  - постоянное для данной реакции число, называемое температурным коэффициентом реакции. Для большинства реакций  имеет значение от 2 до 4.

Пример 3: Температурный коэффициент скорости реакции равен 2,6. Во сколько раз возрастет скорость реакции при повышении температуры от 15 до 50 ⁰С ?

Решение:

Поскольку t= t₂ - t₁=50 - 15=35⁰C, то, обозначив скорость реакции при 15 ⁰ и 50 ⁰С соответственно через ₁ и ₂, можем записать:

= 28.

В 28 раз возрастет скорость реакции.

Пример 4. Реакция при температуре 50 ⁰С протекает за 2 минуты 15 секунд. За сколько времени закончится эта реакция при температуре а) 70 ⁰С; б) 20 ⁰С, если в данном температурном интервале температурный коэффициент скорости реакции равен 3 ?

Решение:

а) При увеличении температуры с 50 до 70 ⁰С скорость реакции в соответствии с правилом Вант-Гоффа возрастает:

,

то есть скорость реакции увеличивается в 9 раз.

В соответствии с определением скорость реакции обратно пропорциональна времени реакции, следовательно:

;

б) При уменьшении температуры с 50 до 20 ⁰С скорость реакции в соответствии с правилом Вант-Гоффа уменьшается:

,

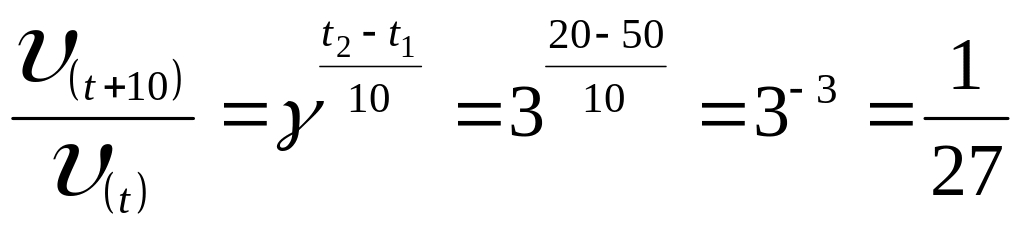то есть скорость реакции уменьшилась в 27 раз.

Более точно влияние температуры на скорость реакции описывается уравнением Аррениуса:

k = k₀e ^(-Ea/RT) , (6)

где k – константа скорости реакции;

k₀ – предэкспоненциальный множитель, отражает частоту столкновений и ориентацию реагирующих частиц;

e – основание натурального логарифма;

E_a – постоянная, называемая энергией активации, определяемая природой реакции. Значения E_a для химических реакций лежат в пределах 40 - 400 кДж/моль.

Уравнение (6) можно представить в виде:

ln k = ln k₀ – E_a/RT (6.1)

или

lg k = lg k₀ - E_a/(2,3 RT) = B - E_a/(2,3 RT) (6.2)

E_a/(2,3 RT) = tg  = lg k/(1/T).

Рис.2

Уравнение Аррениуса позволяет проводить более точные расчеты изменения скорости реакции с увеличением температуры, чем уравнение (5). Приведем уравнение Аррениуса для двух температур:

lg k₁ = lg k₀ – E_a/(2,3 RT₁);

lg k₂ = lg k₀ – E_a/(2,3 RT₂).

Вычитая из второго уравнения первое, получаем:

(7.1)

или

. (7.2)

Из уравнений (5) и (7) следует, что  = (k₂/k₁) и T = 10.

.

Расчеты показывают, что , равное 2-4, соответствует Е_а = 57 - 114 кДж/моль для Т₁ = 300К и Е_а = 236 - 472 кДж/моль для Т₂ = 500К.

Отсюда следует, что правило Вант-Гоффа (5) соблюдается для ограниченного круга реакций, протекающих при температурах, близких к комнатным.

Уравнение Аррениуса позволяет рассчитывать константы скорости (и скорости) реакции при различных температурах.

В ходе химической реакции разрушаются одни и возникают другие молекулы и соединения, происходит изменение химических связей, то есть перераспределение электронной плотности. Если бы старые химические связи в ходе реакции сразу полностью разрушались, то на это потребовалось бы большое количество энергии и реакция протекала крайне медленно. Как показали исследования, в ходе реакции система проходит через переходное состояние, через образование так называемого активированного комплекса. Например, ход реакции AB + DC = AD + BC можно представить схемой:

A  B A - - - B A B

  ¦ ¦    

D  C D - - - C D C