7.2. Истечение жидкости из отверстия в тонкой стенке при установившемся движении (жидкости).

Истечение жидкости в газовую среду при атмосферном давлении. При истечении из

отверстия в тонкой стенке криволи­нейные траектории частиц жидкости сохраняют свою форму и за пределами отверстия, т.е. после выхода из отвер­стия сечение струи уменьшается и дос­тигает минимальных значений на рас­стоянии равном (d - диаметр отверстия). Таким образом, в сечении 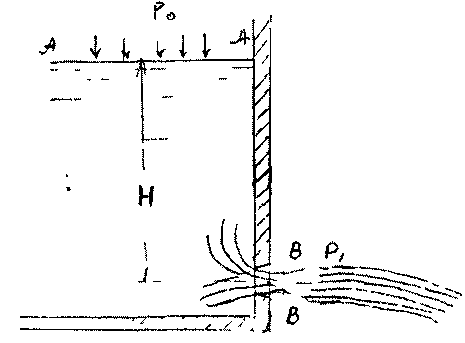В - В будет находиться как назы­ваемое сжатое сечение струи жидкости. Отношение площади

чения струи к площади отверстия называется коэффсщииитоживинфиясфэ&мзвтачаетр^ивсек

гда:

где: s - площадь отверстия,

з_сж - площадь сжатого сечения струи, s - коэффициент сжатия струи.

Запишем уравнение Бернулли для двух сечений А -А и В -В. В связи с тем, что от­верстия в стенке является малым сечение В -В можно считать «горизонтальным» (ввиду малости отверстия), проходящим через центр тяжести сжатого сечения струи.

i. *"*

Поскольку величина скоростного напора на свободной поверхности жидкости (сече­ние А - А) мала из-за малости скорости, то её величиной можно пренебречь. В данном случае истечение жидкости происходит в атмосферу, следовательно р_{ - р₀. Тогда:

^т г

F> f

Поскольку в тонкой стенке потери напора по длине бесконечно малы, то

где' - коэффициент потерь напора в тонкой стенке Следовательно, скорость в сжатом сечении струи будет равна:

Первый сомножитель в равенстве носит название коэффициента скорости'

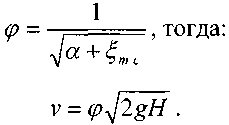
Определим расход жидкости при её истечении из отверстия (заметим, что скорость истечения жидкости у нас относится к площади сжатого живого сечения струи):

где: - называется коэффициентом расхода.

При изучении процесса истечения жидкости предполага­лось, что ближайшие стенки и дно сосуда находятся на достаточ­но большом удалении от отверстия: , т.е. не ближе 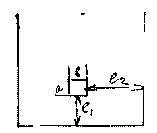тройного расстояния от направляющих стенок. В этом случае все линии тока имеют одинаковую кривизну, и такое сжатие струи

называется совершенным сжатием. В иных случаях близко расположенные стенки явля­ются для струи направляющими элементами, и её сжатие будет несовершенным (не оди-

наковым со всех сторон). В тех случаях, когда отверстие непосредственно примыкает к одной из сторон отверстия (сечение отверстия не круглое), сжатие струи будет неполным. При неполном и несовершенном сжатии струи наблюдается некоторое увеличение коэффициента расхода. При полном совершенном сжатии струи коэффициент сжатия дос­тигает 0,60 - 0,64. Величины коэффициентов сжатия струи, коэффициента расхода зависят

от числа Рейнольдса (см. рисунок), причём коэффициенты сжатия и скорости в разных направлениях: с возрастанием числа Рей­нольдса коэффициент скорости увеличивает­ся, а коэффициент сжатия струи убывает. В результате этого коэффициент расхода оста­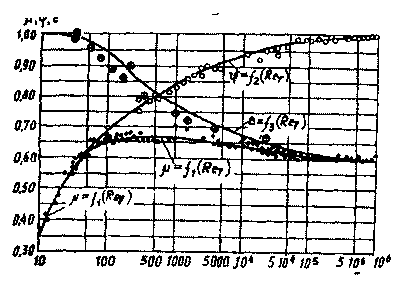 ётся практически неизменным (исключением являются потоки жидкости с весьма малыми числами Рейнольдса).

Величины коэффициента расхода измеряются простым замером фактического расхо­да жидкости через отверстие и сопоставлением его с теоретически вычисленным значени­ем.

Коэффициент сжатия струи измеряется путём непосредственного определения сжа­того сечения струи, коэффициент скорости - по траектории струи.

Истечение жидкости через затопленное отверстие. Истечение через затопленное от­верстие в тонкой стенке, т.е. под уровень жидкости ничем существенным не отличается от истечения в атмосферу.

Пусть в резервуаре имеется перегородка с отверстием, уровни жидкости находятся

на отметках и относи­тельно плоскости сравнения, проходящей через центр тя­жести отверстия. Запишем уравнение Бернулли для свободных поверхностей жидкости (сечение А - А и сечение В - В относительно 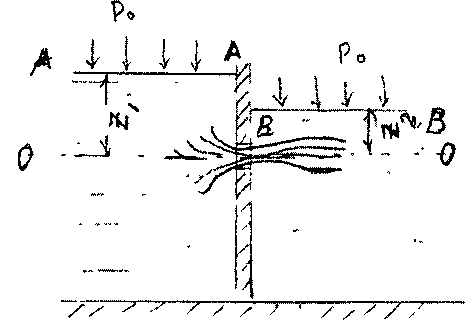плоскости сравнения О - О).

Потери напора состоят из двух частей: потеря напора при истечении из отверстия в тонкой стенке (как при истечении в атмосферу):

и потеря на внезапное расширение струи от сжатого сечения до сечения резервуара:

^р *

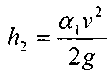Подставив полученные выражения для видов потерь в предыдущее уравнение, полу­чим:

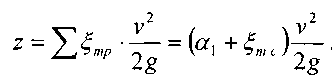
В данном случае действующим напором является разность уровней свободных по­верхностей жидкости z. Скорость истечения будет равна:

j * * *

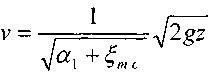Обозначив: получим выражение для расхода жидкости¹

•>
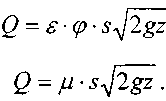