6. Определение основных параметров конической передачи
К основным параметрам относят: главный параметр – диаметр основания делительного конуса колеса de2, передаточное число u, внешний торцовый модуль mte, ширину венца b и угол наклона линии зуба βm в середине ширины зубчатого венца.
Предварительное значение диаметра основания делительного конуса колеса по формуле:
,
(6.1)
Расчётный момент определяем по формуле:
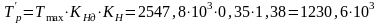Н·мм.
Определяем
коэффициент
по табл. 4.18 [ ] в зависимости от соотношения
способов упрочнения зубьев шестерни и
колеса:
.
мм
В соответствии с единым рядом главных параметров принимаем ближайшее стандартное значение dе2 = 280 мм.
Уточняем фактическую скорость по формуле:
,
(6.2)
м/с,
и коэффициенты КНα = 1, КНυ = 1, КНβ = 1,38, то окончательное значение коэффициента нагрузки:
КН = 1 · 1,38 · 1 = 1,38.
Фактическое контактное напряжение:
,
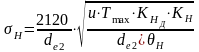(6.3)
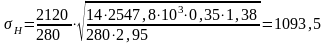МПа.
Перегрузок по напряжению нет.
Определяем число зубьев колеса по формуле:
,
(6.4)
где К – коэффициент по табл. 4.18 [ ], К = 14,0.
.
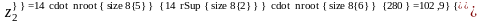Число зубьев шестерни определяем по формуле:
,
(6.5)
Принимаем
z1
= 12;
.
Ближайшее целое число z2
= 168.
Фактическое передаточное число:
.
Торцовый модуль определяем по формуле:
,
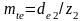(6.6)
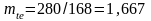мм.
Напряжение изгиба определяем по формуле:
.
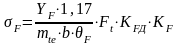Сначала проверяем колесо, которое слабее шестерни.
Угол делительного конуса определяем по формуле:
,
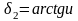(6.7)
°.
Биэквивалентное число зубьев колеса при βm = 35° определяем по формуле:
,
(6.8)
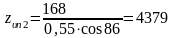
Относительное смещение по табл. 4.19 [ ] xn2 = - 0,42 для z1 = 12.
Коэффициент формы зуба колеса по табл. 4.13 [ ] YF2 = 3,63.
Внешнее конусное расстояние определяем по формуле:
,
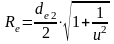(6.9)
мм.
Ширину венца определяем по формуле:
,
(6.10)
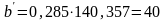мм.
Принимаем b = 90 мм.
По табл. 4.18 [ ] определяем коэффициент θF:
.
Определяем окружную силу по следующей формуле:
,
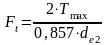(6.11)
Н.
Коэффициент долговечности KFд = 0,98.
Коэффициент нагрузки по формуле .
Коэффициент
распределения нагрузки
= 0,81.
Начальный
коэффициент концентрации
= 1,67.
Коэффициент концентрации определяем по формуле:
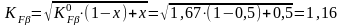
Коэффициент динамичности по табл. 4.12 [ ] для υm = 0,9 м/с = 1,01.
Следовательно,
Определим напряжение изгиба
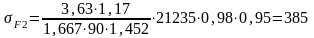МПа.
Допускаемое напряжение по табл. 4.6 [ ] равно:
МПа
> σF2
Проверяем статическую прочность. Наибольшее допускаемое напряжение по табл. 4.6 [ ] [σF2max] = 1200 МПа.
Проверяем прочность зубьев шестерни на изгиб по формуле:
,
(6.12)
.
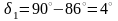Биэквивалентное число зубьев шестерни:
,
(6.13)
.
Относительное смещение xn1 = 0,42.
Коэффициент формы зуба по табл. 4.13 [ ] YF1 = 3,50.
Напряжение изгиба:
МПа.
Допускаемое напряжение по табл. 4.6 [ ] для стали марки 18ХГТ [σF1] = 600 МПа > σF1.
При высоком перепаде твёрдости шестерня недогружена.
Окончательные параметры передачи:
Таблица 8
№ п/п |
Наименование параметра |
Обозначение |
Численное значение |
1 |
Диаметр основания делительного конуса колеса |
de2 |
280 мм |
2 |
Фактическое передаточное число |
u |
14 |
3 |
Ширина венца |
b |
90 мм |
4 |
Внешний торцовый модуль |
mte |
1,667 мм |
5 |
Число зубьев шестерни |
z1 |
12 |
6 |
Число зубьев колеса |
z2 |
168 |
7 |
Угол наклона линии зуба |
β |
35° |
8 |
Относительное смещение |
xn1 = -xn2 |
0,42 |
9 |
Угол делительного конуса |
δ1 |
4° |
10 |
Угол делительного конуса |
δ2 |
86° |
11 |
Внешнее конусное расстояние |
Re |
140,357 мм |