3. Общая постановка задачи исследования операции.

Все факторы, входящие в описание операции, можно разделить на две группы:

• постоянные факторы (условия проведения операции) α₁, α₂, …, на которые влиять не может;

• зависимые факторы (элементы решения) x₁, x₂, … , которые в известных пределах исследователь может выбирать по своему усмотрению.

Целевая функция Z зависит от факторов обеих групп:

Оптимизационную задачу можно сформулировать в общем виде: найти переменные x₁, x₂, … x_n, удовлетворяющие системе неравенств

(1.1)

и обращающие в максимум (или минимум) целевую функцию, т.е.

(1.2)

Условия неотрицательности переменных, если они есть, входят в ограничения (1.1). Эти условия определены физической сущностью переменных.

Как известно, упорядоченная совокупность значений п переменных x₁, x₂, … , x_n представляется точкой n-мерного пространства. В дальнейшем эту точку будем обозначать , а само оптимальное решение .

Частным случаем общей задачи (1.1) - (1.2) на определение экстремума функции п переменных при некоторых ограничениях, т.е. задачей на условный экстремум, является классическая задача потребления.

Пусть имеется п видов товаров и услуг, в количестве x₁, x₂, … , x_n по ценам соответственно p₁, p₂, … , p_n за единицу. Суммарная стоимость этих товаров и услуг составляет Уровень потребления Z может быть выражен некоторой функцией полезности Необходимо при данной величине доходов I найти такой набор товаров и услуг x₁, x₂, … , x_n, чтобы обеспечить максимальный уровень потребления, т.е.

(1.3)

при условии (1.4)

(1.5)

Решения этой задачи, зависящие от цен p₁, p₂, … , p_n и величины дохода I, называются функциями спроса.

В тех случаях, когда функции f и φ_i в задаче (1.1) - (1.2) хотя бы дважды дифференцируемы, можно применять классические методы оптимизации. Однако применение этих методов в исследовании операций весьма ограниченно, метод дает возможность определить локальный экстремум, а из-за многомерности функции определение ее максимального (или минимального) значения (глобального экстремума) может оказаться трудоемким, причем экстремум возможен на границе области решений. Классические методы не работают, если множество допустимых значений аргумента дискретно или функция Z задана таблично. В этих случаях для решения задачи применяются методы математического программирования.

4. Классификация задач исследования операций

1. Если критерий эффективности 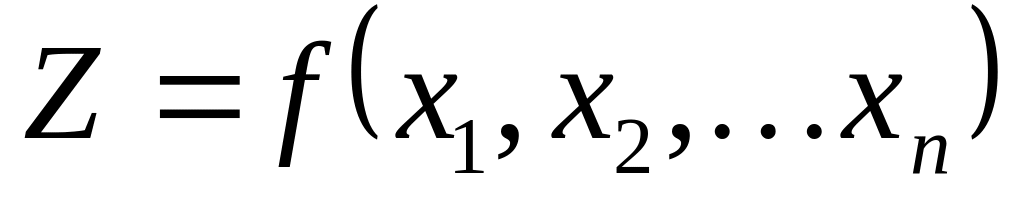является линейной функцией, и функции в системе ограничений также линейны, то задача является задачей линейного программирования.

2. Если, исходя из содержательного смысла, ее решения должны быть целыми числами, то имеем задачу целочисленного линейного программирования.

3. Если критерий эффективности или система ограничений задаются нелинейными функциями, то это задача нелинейного программирования.

4. Если указанные функции обладают свойствами выпуклости, то задача является задачей выпуклого программирования.

5. Если в задаче математического программирования имеется переменная времени и критерий эффективности выражается через уравнения, описывающие протекание операций во времени, то такая задача является задачей динамического программирования.

6. Если функции f и (или) φ_i зависят от параметров, то получаем задачу параметрического программирования.

7. Если функции f и (или) φ_i носят случайный характер, то это задача стохастического программирования.

8. Если точный оптимум найти алгоритмическим путем невозможно из-за чрезмерно большого числа вариантов решения, то прибегают к методам эвристического программирования, позволяющим существенно сократить просматриваемое число вариантов и найти если не оптимальное, то достаточно хорошее с точки зрения практики решение.

Из перечисленных методов математического программирования наиболее распространенным и разработанным является линейное программирование. Его методы применимы для широкого круга задач.

На практике в большинстве случаев эффективность операции оценивается не по одному, а сразу по нескольким критериям, одни из которых следует максимизировать, другие — минимизировать. Математический аппарат может принести пользу и в случаях многокритериальных задач исследования операции, по крайней мере, помочь отбросить заведомо неудачные варианты решений. Для того чтобы на основании множества критериев, в том числе и противоречащих друг другу (например, прибыль и расход), составить целевую функцию, необходимо установить приоритет критериев, назначив им весовые коэффициенты. Нахождение множества эффективных (оптимальных по Парето) решений для задачи многокритериальной оптимизации рассматривается, например, в курсе системного анализа. Окончательный выбор «компромиссного» решения (приемлемого по всем критериям) остается за лицом, принимающим решение.