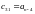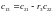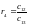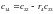- •1 Теоретические основы автоматизации
- •Виды систем автоматического управления.
- •2 Линеаризация нелинейных дифференциальных уравнений
- •3 Передаточная функция
- •4 Переходная, импульсная хар-ка
- •5 Частотные характеристики
- •6 Характеристики дифференцирующего и интегрирующего звеньев.
- •7. Характеристики инерционного (апериодического) звена.
- •8 Характеристики инерционно-дифференцирующего звена.
- •9.Звено постоянного запаздывания.
- •Передаточная функция
- •10. Характеристики форсирующего звена.
- •11.Последовательное и параллельное соединение звеньев.
- •12.Простейшие типовые звенья на операционных усилителях.
- •13. Принципы построения динамических звеньев со сложными передаточными функциями на операционных усилителях (тау)
- •14. Критерий Рауса
- •15. Критерий Гурвица
- •16. Критерий Михайлова
- •17 Критерий Найквиста
- •18. Запасы устойчивости
- •21. Ошибки регулирования
- •22. Прямые показатели качества
- •23. Корневые методы оценки качества
- •24 Определение показателей качества по афчх сау
- •25. Оценка качества сау по показателю колебательности (частотный метод)
- •26. Оценка качества по лачх Оценка качества по ачх замкнутой системы. Допустим, выходной сигнал следящей системы точно копирует входной, (это возможно только в идеальных системах управления) при этом
- •При оценке качества системы по афх и лачх разомкнутой системы получают следующие косвенные показатели качества: Aз – запас устойчивости по амплитуде (модулю); з - запас устойчивости по фазе.
- •Оценка качества по вчх замкнутой системы. Рассмотрим основные свойства вчх.
- •27 Интегральные методы оценки качества
- •28 Коррекция свойств сау изменением коэффициента усиления
- •29 Коррекция свойств сау изменением постоянной времени звена сау
- •25. Оценка качества сау по показателю колебательности (частотный метод)
- •30 Типовые законы регулирования
14. Критерий Рауса
Критерий Рауса более удобен для программирования на ЭВМ. Составляется таблица по определенным правилам: число строк таблицы (n+1), в первые две строки записывают коэффициенты ХУ в соответствии с их индексами. Коэффициента с отрицательными индексами соответствуют нулю.
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для устойчивости САР необходимо и достаточно, чтобы все коэффициенты первого столбца таблицы были положительными. Если не все коэффициенты первого столбца положительны, то число корней, лежащих в правой плоскости равно числу знакоперемен в этом столбце
15. Критерий Гурвица
Позволяет судить об отсутствии правых корней ХУ по знакам диагональных миноров в определителе Гурвица.
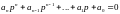
Д ля
составления матрицы Гурвица на главной
диагонали расставляются коэффициенты
ХУ, начиная с
ля
составления матрицы Гурвица на главной
диагонали расставляются коэффициенты
ХУ, начиная с
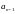 до
до
 .
Порядок матрицы равен порядку ХУ. Затем
столбцы дополняются вверх в порядке
убывания индексов, вниз – в порядке
возрастания. Члены столбцов с индексами,
больших чем n
и меньше 0 равны 0.
.
Порядок матрицы равен порядку ХУ. Затем
столбцы дополняются вверх в порядке
убывания индексов, вниз – в порядке
возрастания. Члены столбцов с индексами,
больших чем n
и меньше 0 равны 0.
Необходимым и достаточным условием устойчивости системы является положительность всех диагональных миноров определителя Гурвица.
Важным
условием устойчивости является
положительность последнего диагонального
минора
 :
:
-
если
 ,
то система имеет нулевой корень и она
находится на границе апериодической
устойчивости
,
то система имеет нулевой корень и она
находится на границе апериодической
устойчивости
-
если
 ,
и выполняются все остальные условия,
то система находится на границе
колебательной устойчивости.
,
и выполняются все остальные условия,
то система находится на границе
колебательной устойчивости.
Эти условия используют для определения граничных значений и областей устойчивости.
Для систем выше 4 порядка критерий Гурвица сложно использовать вследствие громоздкости вычислений.
16. Критерий Михайлова
В основу критерия Михайлова лежит принцип аргумента комплексного переменного.
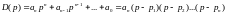
Каждому корню на комплексной плоскости соответствует точка:
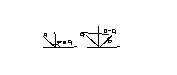
Направим
вектор p
по мнимой оси, это будет соответствовать
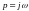 ,
тогда конец вектора
,
тогда конец вектора
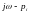 будет лежать на мнимой оси, поворачиваясь
в направлении, зависящем от положения
корня на плоскости.
будет лежать на мнимой оси, поворачиваясь
в направлении, зависящем от положения
корня на плоскости.
Для
левых корней: при изменении частоты от
 до
до
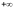 вектор
перемещается в направлении против
часовой стрелке, причем его аргумент
получает приращение
вектор
перемещается в направлении против
часовой стрелке, причем его аргумент
получает приращение
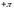 ,
т.е.
,
т.е.

Для
правых корней:

Если все корни лежат в левой плоскости, то:
 (*)
(*)
Если
среди n
корней ХУ, имеется m
– правых корней, а (n-m)
– в левой, то при изменении частоты от
 то
то
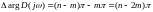
Для того чтобы системы была устойчивой необходимо и достаточно, чтобы выполнялось условие (*).
При практическом использовании этого правила, ХУ разделяют на мнимую и действительную части:
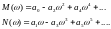
Ввиду
того что
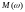 - четная, а
- четная, а
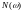 - нечетная, будем строить годограф для
- нечетная, будем строить годограф для
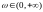 .
.
Для
устойчивости САР необходимо и достаточно,
чтобы годограф вектора W(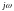 ),
начиная при
),
начиная при
 на действительной оси с ростом частоты
проходил в положительном направлении
(против часовой стрелки) последовательно
n
квадрантов на комплексной плоскости,
где n
– порядок ХУ.
на действительной оси с ростом частоты
проходил в положительном направлении
(против часовой стрелки) последовательно
n
квадрантов на комплексной плоскости,
где n
– порядок ХУ.
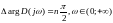
Для устойчивости системы необходимо и достаточно выполнение следующих условий:
1.
2.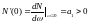
3.
Между двумя любыми корнями
 лежит один из корней
лежит один из корней

Если годограф проходит через начало координат – ХУ имеет нулевой корень