Ввести зависимости для ограничений (рис 3)

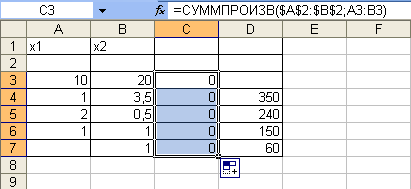
• Поместить курсор в ячейку С3

• На панели инструментов кнопка Копировать в буфер

• Поместить курсор в ячейку С4

• На панели инструментов кнопка Вставить из буфера

• Поместить курсор в ячейку С5

• На панели инструментов кнопка Вставить из буфера

• Поместить курсор в ячейку С6

• На панели инструментов кнопка Вставить из буфера

• Поместить курсор в ячейку С7

• На панели инструментов нажать кнопку Вставить из буфера

(содержимое ячеек С4-С7 необходимо проверить. Они обязательно должны содержать информацию, как показано

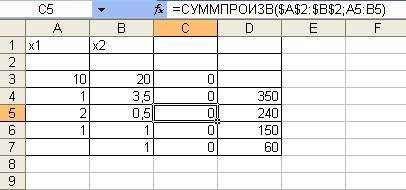
В строке меню указатель мыши поместить на сервис. В развернутом меню выбрать команду Поиск решения. Появится диалоговое окно Поиск решения

Появляется диалоговое окно «Поиск решения»

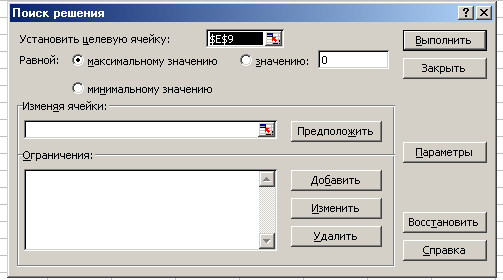
Выбрать режим Сервис Поиск решения

6. Назначить ячейку для целевой функции (установить целевую ячейку) ,указать адреса изменяемых ячеек.

• Поместить курсор в строку Установить целевую ячейку.

• Ввести адрес ячейки $C$3

• Ввести тип целевой функции в зависимости от условия вашей задачи. Для этого отметьте, чему равна целевая функция – в данной задаче мы ищем максимальную прибыль, значит мах

• Поместить курсор в строку Изменяя ячейки

• Ввести адреса искомых переменных A$2:B$

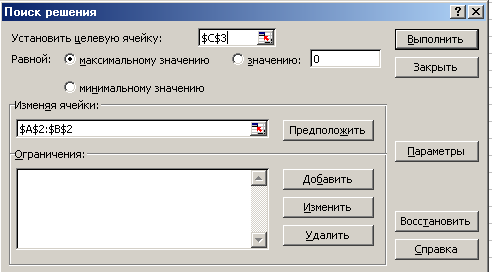
7. Ввести ограничения

• Поместить указатель мыши на кнопку Добавить. Появляется диалоговое окно Добавление ограничений

• В строке Ссылка на ячейку ввести адрес $C$4

• Ввести знак ограничения.

• В строке Ограничения ввести адрес $D$D

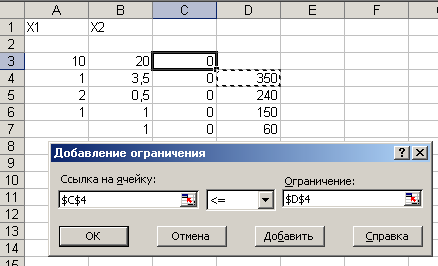
• Поместить указатель мыши на кнопку Добавить. На экране появится диалоговое окно Добавление ограничения

• Ввести остальные ограничения по вышеописанному алгоритму

• После введения последнего ограничения нажать на кнопку Ок

• На экране появится диалоговое окно Поиск решения с введенными условиями

8. Ввести параметры для решения задачи линейного программирования

• В диалоговом окне поместить указатель мышки на кнопку Параметры. На экране появится диалоговое окно Параметры поиска решения

Нажать кнопку ОК и в появившемся окне режим Выполнить.

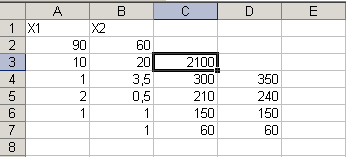
Получим исходную таблицу с заполненными ячейками A3:B3 для значений x_i и ячейка C3 с максимальным значением целевой функции ( максимальной прибылью)

Если выбрать тип отчета Устойчивость то можно получить дополнительную информацию об оптимальном решении.

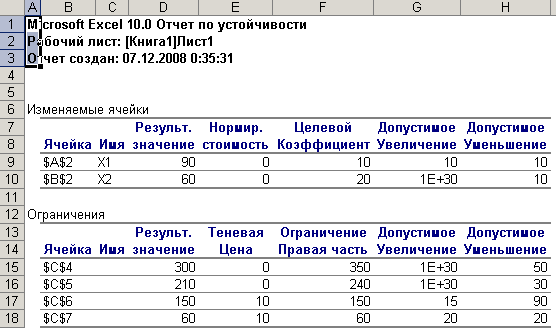
В результате решения щзадачи был получен ответ : необходимо сшить 70 шт. женских костюмов и 80 шт. мужских костюмов, чтобы получить максимальную прибыль 2300 у.е.

Задание1. Вам как специалисту финансового менеджмента необходимо провести моделирование процесса получения максимальной прибыли и производства продукции:

1. Создать в своей тетради таблицу вида :

2. Менять по очереди каждый из параметров (кроме 1 дня трудозатрат на 1 костюм) и записывать в таблицу исходные данные и результаты варианта

3. Составить 10 вариантов модели

4. Провести анализ при каких заданных параметрах можно получить максимальную прибыль и при каких минимальных затратах

5. Сделать вывод, как работать предприятию

Пз 3 (часть2) Лабораторная работа № 4 Оптимизационные модели в задачах экономики

1. Задача об использовании сырья.

Рассмотрим компьютерную модель решения данной задачи об использовании сырья.

Технология работы:

1. Открыть папку «Решение задач симплекс-методом», затем запустить программу, с помощью значка

2. Появится окно программы, в таблицу которого внести рассмотренные выше данные.

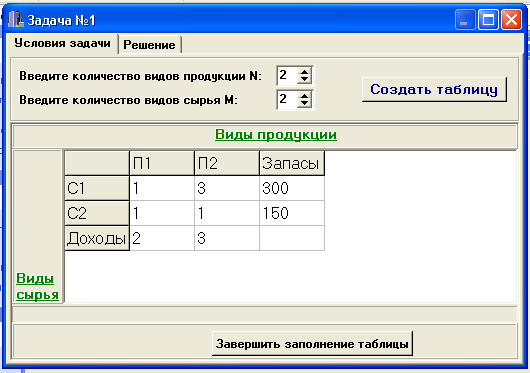
2. Выбрать режим «Завершить заполнение таблицы « и далее «Решение».

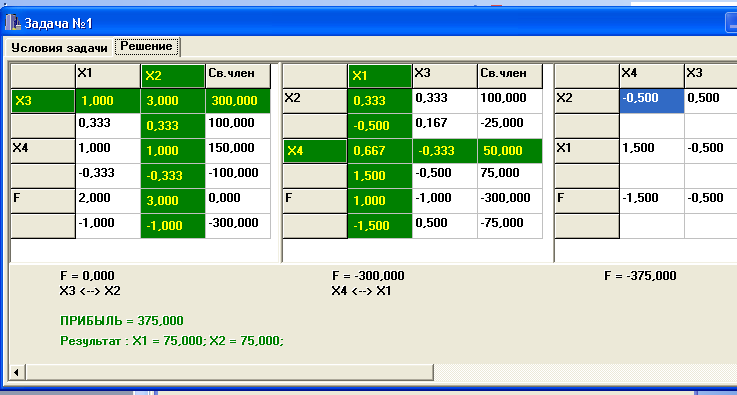
Появится таблица , из которой следует , что максимум целевой функции (или прибыль предприятия от реализации продукции, в данном случае двух видов ) = 375 при расходе сырья на единицу продукции первого вида П1 ( =75) и второго вида П2 (

Задача 2. Трикотажная фабрика использует для производства свитеров и кофточек чистую шерсть, силон и нитрон, запасы которых составляют соответственно ,800,400 и 300 кг. Количество пряжи (кг.) необходимое для изготовления 10 изделий, а также прибыль, получаемая от их реализации приведены в таблице.

Вид сырья в пряже	Затраты пряжи на 10 шт.
	Свитер	Кофточка
Шерсть	4	2
Силон	2	1
Нитрон	1	1
Прибыль, руб	6	5

Составьте план производства изделий, обеспечивающий получение максимальной прибыли.

Решение.

Технология работы:

1. Открыть папку «Решение задач симплекс-методом», затем запустить программу, с помощью значка

2. Появится окно программы, в таблицу которого внести рассмотренные выше данные.

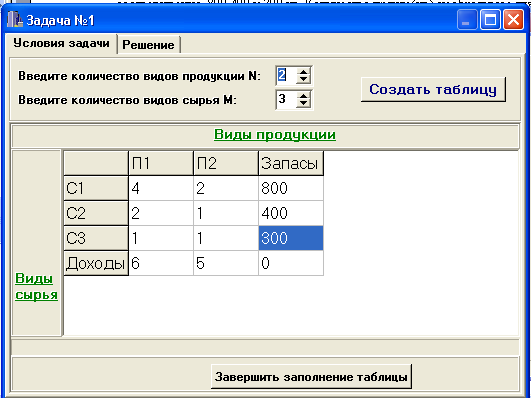
2. Выбрать режим «Завершить заполнение таблицы « и далее «Решение».

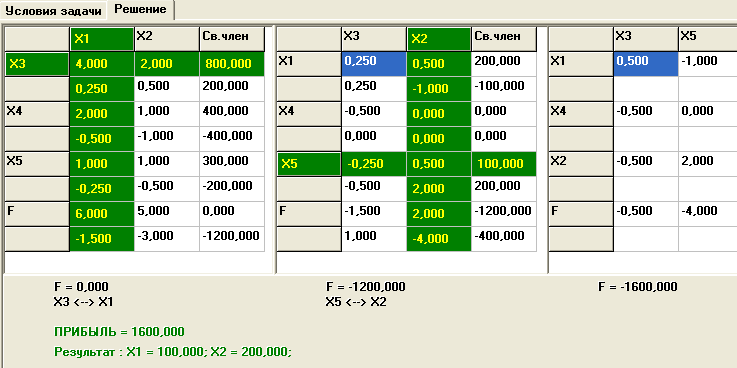
Появится таблица , из которой следует , что максимум целевой функции (или прибыль предприятия от реализации продукции, в данном случае двух видов ) = 1600 при производстве свитеров П1 ( =100) и кофточек П2 (

Задание. Смоделируйте прибыль при других расходах и прибыли.

2. Задача о диете

Задачей о диете называется задача линейного программирова­ния, состоящая в определении такого рациона (набора продуктов питания), который удовлетворял бы потребности человека (напри­мер, при питании работников некоторого предприятия) в необхо­димых питательных веществах при минимальной общей стоимости приобретаемых продуктов питания. Эта задача является частным случаем более общей задачи об оптимальном составе смеси.

В общем виде задача о диете формулируется следующим обра­зом. Пусть — количество продукта питания -го вида; — цена единицы продукта питания -го вида; n - количество видов продуктов пита­ния (j = 1,n). Известны нормы потребления (не менее) каждого из т типов питательных веществ, которые обозначены , и содержание питательных веществ каждого типа в единице продукта каждого вида, которое обозначается величиной . Требуется опре­делить количества продуктов питания каждого вида, обеспечивающих нормы потребления всех питательных веществ и имеющих наименьшую общую стоимость.

Экономико-математическая модель данной задачи имеет вид:

(2.29)

(2.30)

(2.31)

Пример 1. Комбинат питания предприятия решает задачу о наименьшей стоимости двух приобретаемых продуктов питания для работников предприяития. Цены этих продуктов, содержание обязательных в рационе двух типов питательных веществ в единице приобретаемых продуктов и нормы их потребления (не менее ) в условных единицах заданы в таблице 3.

Решение

Пусть -количества приобретаемых продуктов каждого вида. Тогда целевая функция и ограничения задачи будут иметь вид:

Рассмотрим компьютерную модель решения данной задачи об использовании сырья.

Технология работы:

1. Открыть папку «Решение задач симплекс-методом», затем запустить программу, с помощью значка

2. Появится окно программы, в таблицу которого внести рассмотренные выше данные.

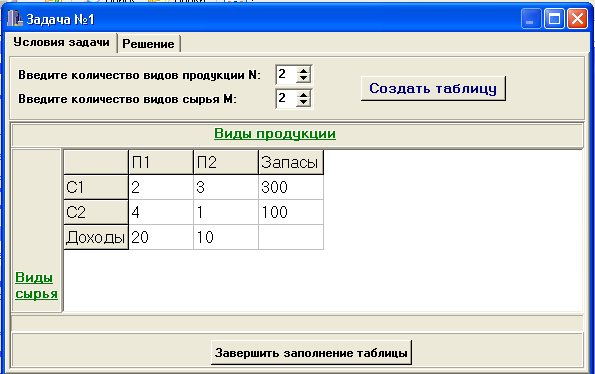
2. Выбрать режим «Завершить заполнение таблицы « и далее «Решение».

Появится таблица , из которой следует , что максимум целевой функции = 1000 при расходе сырья на единицу продукции первого вида П1 ( =00) и второго вида П2 (

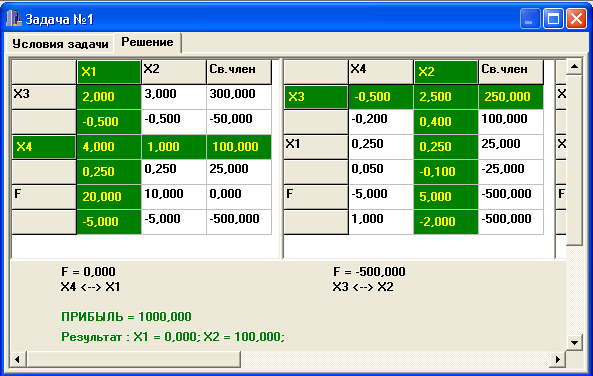
Задание 1. провести моделирование при иных запасах.

Пример 2. Для откорма крупного рогатого скота используется два вида кормов В1 и В2 в которые входят питательные вещества Ф1, Ф2, Ф3, Ф4. Содержание количества единиц питательных веществ в одном килограмме каждого корма , стоимость одного килограмма корма и норма содержания питательных веществ в дневном рационе животного представлены в таблице

Составьте рацион при условии минимальной стоимости

Задание. Записать решение самим.

Лабораторная работа 5 Балансовая задача.

Задача 1. Даны коэффициенты прямых затрат аij конечный продукт Y_i для трехотраслевой экономической системы:

0,3 0,1 0,4

А= 0,2 0,5 0,0

0,3 0,1 0,2

Требуется определить:

• коэффициенты полных затрат

• вектор валового выпуска

• межотраслевые поставки продукции

• проверить продуктивность матрицы А

• заполнить схему межотраслевого баланса

В таблице 2.2 приведены результаты решения задачи по первым трем пунктам

Технология работы:

1. Вычислим матрицу коэффициентов полных затрат B=(E-A)^-1

Для чего внесем в таблицу Excel в строки В2:D4 коэффициенты и вспомним, что единичная матрица , в данном случае 1 0 0

Е = 0 1 0

0 0 1

Соответственно вычтем и занесем эти значения в строки b6:D8

Для вычисления обратной матрицы необходимо:

• выделить диапазон ячеек для размещения обратной матрицы

• выбрать функцию МОБР в категории «Математические»

• ввести диапазон ячеек, где содержится матрица E-A

• нажать клавиши CTRL+SHIFT+ENTER

В ячейки B6:D8 записать элементы матрицы Е-А. Массив Е-А задан как диапазон ячеек. Выделить диапазон В10: D12 для размещения обратной матрицы B=(E-A)^-1

И введем формулу для вычислений МОБР (B6:D8). Затем следует нажать клавиши CTRL+SHIFT+ENTER

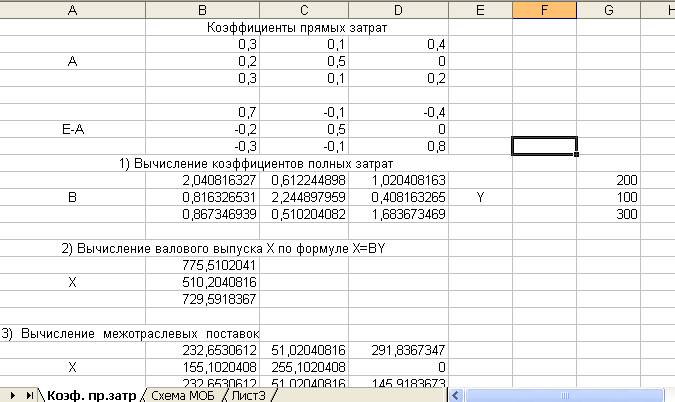
Все элементы матрицы коэффициентов полных затрат В неотрицательны, следовательно , матрица А продуктивна (это ответ на пункты а-г)

1. Вычислим вектор валового выпуска Х по формуле Х=ВУ

2. Для умножения матриц необходимо:

• выделить диапазон ячеек для размещения результата умножения матриц;

• выбрать функцию МУМНОЖ в категории Маиематические;

• ввести диапазон ячеек, где содержится матрицы В и У;

• нажать клавиши Ctrl+SHIFT+ENTER

В ячейки G10:G12 запишем элементы вектора конечного продукта У.

Выделим диапазон В15:В17 для размещения вектора валового выпуска Х, вычисляемого по формуле Х=(Е-А)^-1У

Затем вводим формулу для вычислений МУМНОЖ (В10: D12,G10:G12)

Далее следует нажать клавиши CTRL+SHIFT+ENTER.

3. Межотраслевые поставки х_ij вычисляем по формуле x_ij=a_ijX_j

4. Заполняем схему МОБ (табл. 2.3)

Табл. 2.3

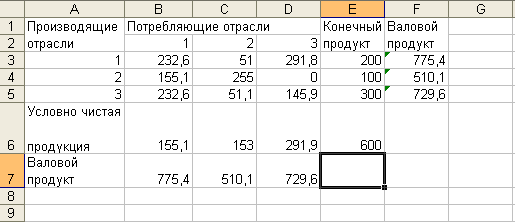
Задание 1.

В таблице даны коэффициенты прямых затрат а_ij и конечный продукт Y_j . Требуется определить:

1. межотраслевые поставки продукции

2. проверить продуктивность матрицы А

3. заполнить схему межотраслевого баланса.

Таблица 2.6.

16