Принцип экстремума для уравнений теплопроводности.

При рассмотрении процесса распространения тепла в областях, ограниченных необходимо учитывать не только начальное распределение температуры, но и те процессы, которые происходят на границе этой области. Границу области в пространстве любой размерности будем обозначать через Γ, а саму область Ω. В зависимости от задания условий на границе различают три типа граничных (смешанных) задач.

1) – первая граничная задача.

2) – вторая граничная задача. Где – нормаль в точках границы.

3) – третья краевая задача.

Рассмотрим задачу: 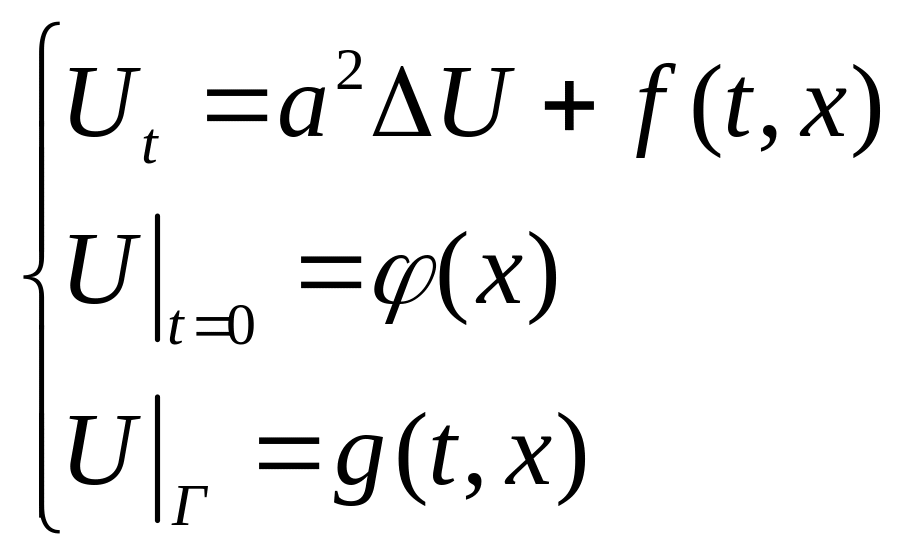, где . Обозначим через , .

Принцип: Функция удовлетворяющая уравнению в цилиндре и непрерывна вплоть до его границы принимает своё наибольшее и наименьшее значение либо на нижнем основании цилиндра (область Ω ), либо на его боковой поверхности.

Док-во.

Рассмотрим только случай максимума.

Допустим, что максимальное значение функции достигается в некоторой внутренней точке цилиндра.

Введём в рассмотрение вспомогательную функцию . При достаточно малом функцию можно рассматривать как приближённое решение уравнения теплопроводности. Найдём погрешность, с которой функция удовлетворяет уравнению теплопроводности .

(1).

Предположим, что функция принимает максимальное значение во внутренней точке цилиндра в этой точке производные первого порядка должны обратиться в нуль.

; ; ; .

Это означает, что во внутренней точке цилиндра максимума не имеет.

Допустим, что максимум достигается на верхнем основании. Тогда в этой точке . Точка и на верхнем основании функция не может принимать максимальное значение.

Функция в силу её выбора является непрерывной вплоть до границы. Максимум достигается либо внутри цилиндра, либо на боковой поверхности:

, где нижнее основание + боковая поверхность. Если

Конец док-ва.

Единственность решения задачи Коши для уравнения теплопроводности.

Рассмотрим задачу (t,x)=[0,T]×Ω Rⁿ

Эта задача имеет бесконечное множество решений. Рассмотрит подмножество решений, будем рассматривать |U(t,x)| M (т.е. будем рассматривать ограниченные решения).

Теорема: (Задача Коши для уравнения теплопроводности)

Она имеет не более одного ограниченного решения.

Начало доказательства. Допустим противное - два различных ограниченных решения задачи Коши. Обозначим через .

Тогда V является решением задачи (1)

Так как U₁ и U₂ ограниченны, то |V| |U₁|+|U₂| |2M|=M₁ (V-ограниченно). Очевидно V 0 является решением задачи (1). Покажем, что других решений эта задача не имеет. Для этого рассмотрим вспомогательную функцию W= ||x||²+ t. Подберём и таким образом, чтобы функция удовлетворяла уравнению теплопроводности V_t-a²∆V=0 β=a²α*2n.

w= (||x||²+2na²t) удовлетворяет уравнению теплопроводности.

Потребуем теперь, чтобы функция w мажорировала решение задачи (1). Т.к. решение задачи (1) ограничено, то есть |V| M₁ , достаточно положить следующее M₁ Т.к. w- решение уравнения теплопроводности, то к нему применим принцип максимума M₁ Ω:||x||²≤L

Положим α = , если . Решение ограниченное и единственное.

Конец доказательства.