Единственность и устойчивость решения задачи Коши для волновых уравнений.
Рассмотрим задачу:
Мы знаем, что решение этой задачи может быть получено по формуле Кирхгофа:
либо другим способом.
Возникает вопрос о совпадении решения задачи Коши, получается по формуле и без применения этой формулы. Всегда можно считать a = 1.
Тогда
переходя к задачи
,
Теорема 3: Задача Коши для волнового уравнения имеет не более одного решения.
Док-во.
Допустим противное.
Пусть задача Коши имеет два различных
решения
и
.
Обозначим разность
.
Для определения функции мы получим задачу:
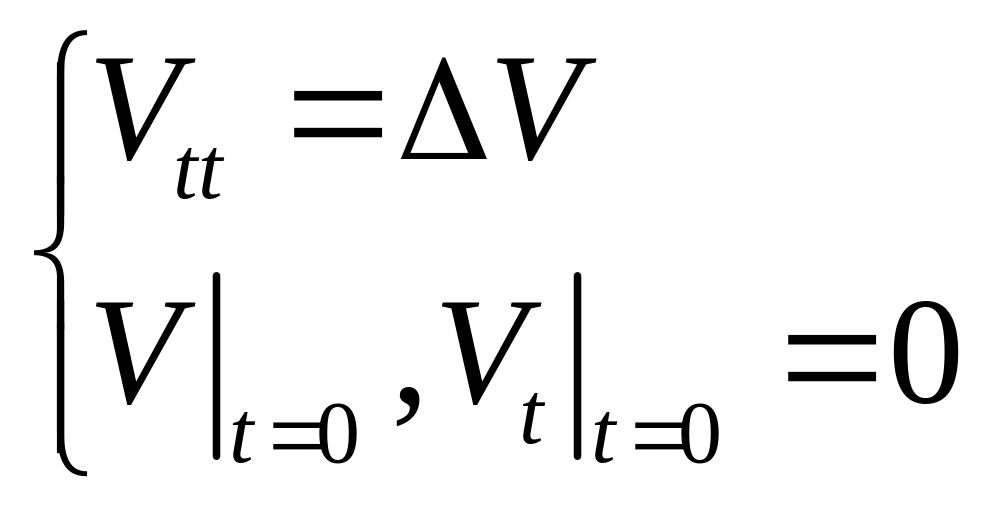
Очевидно, что эта
задача имеет решение
=
0. Нам нужно показать, что других решений
эта задача не имеет. Для большей
наглядности ограничимся случаем двух
переменных т.е. будем рассматривать
уравнение
.
Рассмотрим трёхмерное пространство
.
Взяв в нём
произвольную фиксированную точку
,
через неё, как через вершину проведём
конус
Этот конус
пересекается с плоскостью
.
Проведём ещё плоскость
Проверим тождество:
Тождество проверили.
Объём усечённого конуса обозначим через Ω и проверим последнее тождество.
Если
,
то интеграл в левой части тождество
обращается в нуль.
Вместо
будем
писать
.
.
Так как на
и при начальных условиях
получаем
так как из
.
На верхнем основании
конуса
Тогда
.
Рассмотрим теперь
.
На боковой
поверхности направляющие косинусы
нормали удовлетворяют следующему
соотношению:
.
Это следует из того, что будет написано ниже.
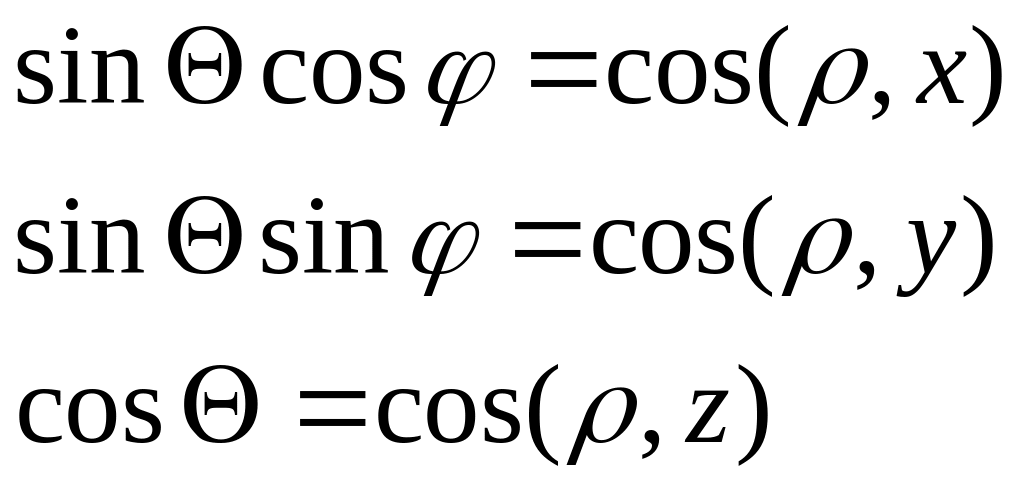
Если сечение
произвольное и
это означает, что в любом сечении
,
а значит и в сечении
Но на нижнем основании
Конец доказательства.
Теорема: Решение задачи Коши устойчиво т.е. малое изменения начальных условий влечёт за собой малое изменение решений.
Начало доказательства.
решение для
решение для
Нам нужно доказать,
что если
и
,
то
Конец доказательства.
Элементарное (фундаментальное) решение уравнения теплопроводности.
Рассмотрим сначала
одномерное уравнение теплопроводности
.
Найти общее решение этого уравнения мы
не можем. Это уравнение имеет бесконечное
множество частных решений. Среди всех
решений свёртка этого решения с единицей
должна давать единицу, т.е.
.
Воспользуемся
преобразованием Фурье, и будем искать
решение
.
Найдём его:
.
Найдём частные
производные:
;
.
Подставляем в
уравнение и получаем:
.
Этот интеграл
равен нулю, если
-
это линейное уравнение первого порядка
в частных производных:
.
Решение
или получим:
;
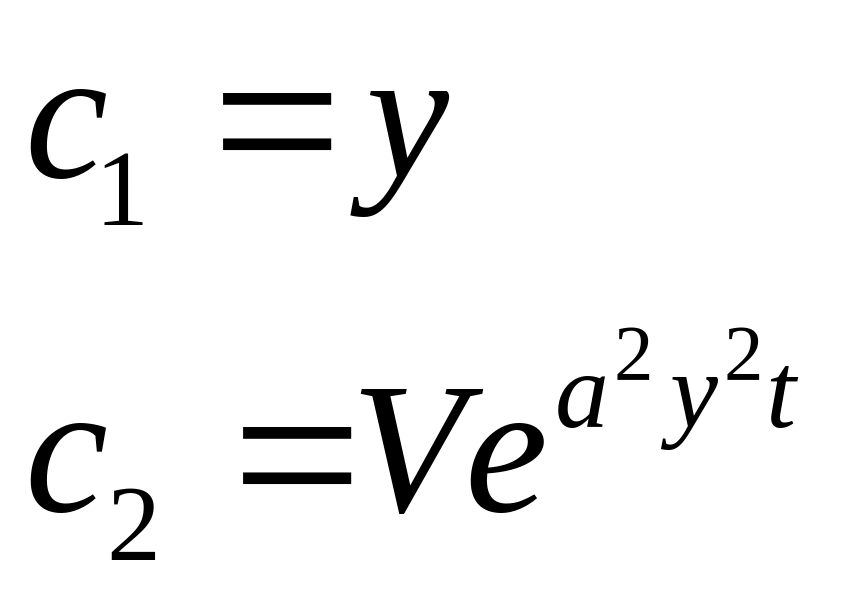
Второй интеграл
этой системы
.
или
.
Положим
(c
= const).
Из Теории Вероятности
интеграл Пуассона
.
Воспользовавшись этим интегралом, получим:
;
;
.
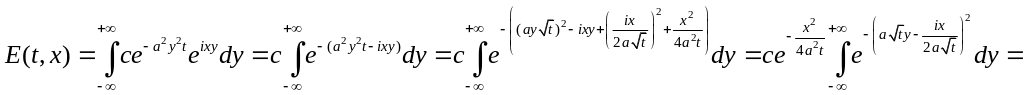
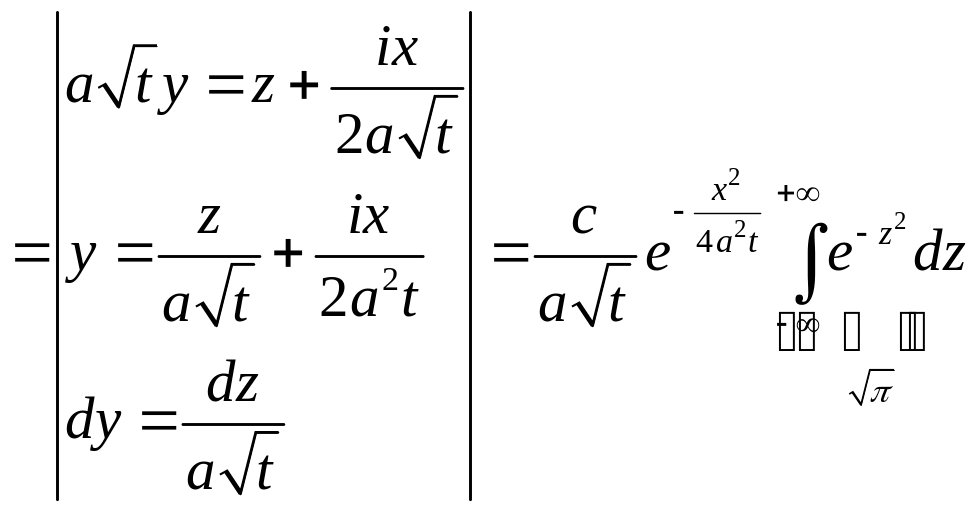Тогда:
И
– фундаментальное
решение уравнения теплопроводности.
Заметим, что чаще
используется не это решение, а функция
,
которая называется функцией
Грина (функцией источника).
Определим теперь
фундаментальное решение уравнение
теплопроводности в случае произвольного
числа пространственных решение, т.е.
,
.
Рассмотрим уравнение
.
Покажем, что функция
является фундаментальным решением
этого уравнения и покажем, что
Находим:
;
.
Получим:
Проверим условие свёртки:
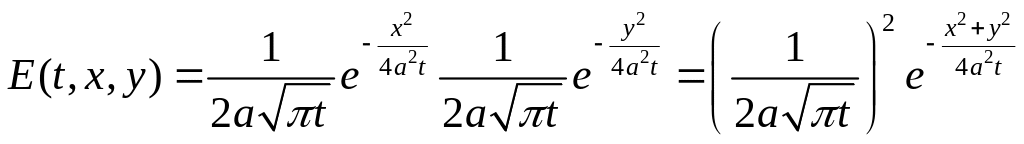– фундаментальное
решение для
двух
пространственных переменных.
.
Эта формула легко обобщается на случай любого числа пространственных переменных.
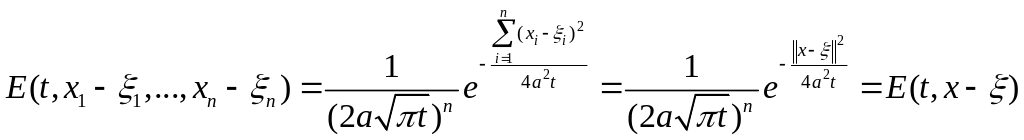
Задача Коши для уравнения теплопроводности.
Пусть имеем задачу
(1)
Решение задачи (1) есть сумма решения двух задач:
(2) 
(3)
Решение задачи (2) есть свёртка начального условия и соответствующей функции источника (функции Грина).
формула Пуассона.
Покажем, что
удовлетворяет уравнению задачи (2) и для
него выполняется начальное условие
этой задачи.
Проверим выполнения начального условия:
Начальное условие выполняется формула Пуассона остаётся верной.
Для решения задачи
(3) воспользуемся принципом Дюамеля,
согласно которому, если
– решение вспомогательной задачи
(4) 
.
То решение задачи (3) определяется
формулой
(5).
;
.
Если подставить решение задачи (3) получим:
.
Функция
удовлетворяет решению уравнения (3). И
решение (3) 
.
Для нахождения
функции
во вспомогательной задаче сделаем
замену
.
(6).
Решение задачи Коши можно определить
с помощью формулы:
.
Пример 1:
.
Отметим, если 
.
Тогда решаем три задачи:
; 
; 
.
.
Вернёмся к примеру и заметим, что
(
)
это линейное уравнение третьего порядка.
,
если при вычислении интеграла Пуассона
участвует некое
.
Пример 2:
.
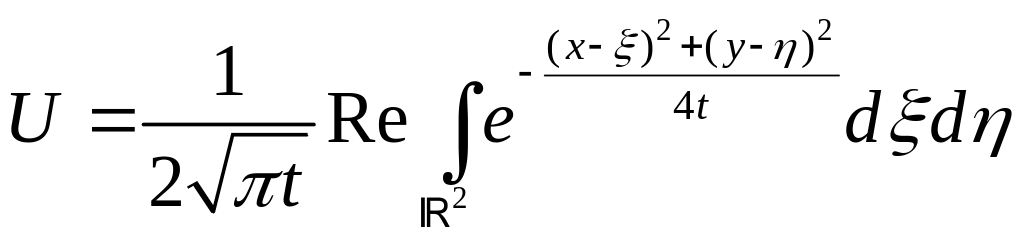