Среднее значение функции на сфере. Решение трехмерного волнового уравнения.
Пусть имеем функцию
по среднему значению этой функции на
сфере радиуса
понимаем выражение:
В дальнейшем нам
понадобится выражение среднего значения
функции
в сферической системе координат.
При переходе к
одной системе координат к другой
необходимо учитывать Якобиан
преобразования. В этом случае:
.
Тогда
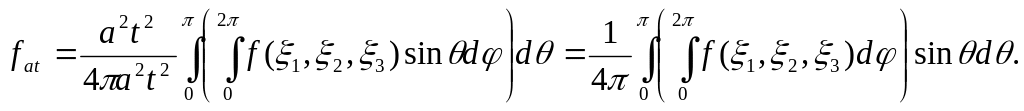
Докажем следующее утверждение:
Утверждение:
(Лемма). Произведение
среднего значения на сфере произвольной
достаточно гладкой функции радиуса
с центром в точке
на время является решением уравнения
или
Доказать, что
решение.
Доказательство:
Найдем
сначала
Найдем
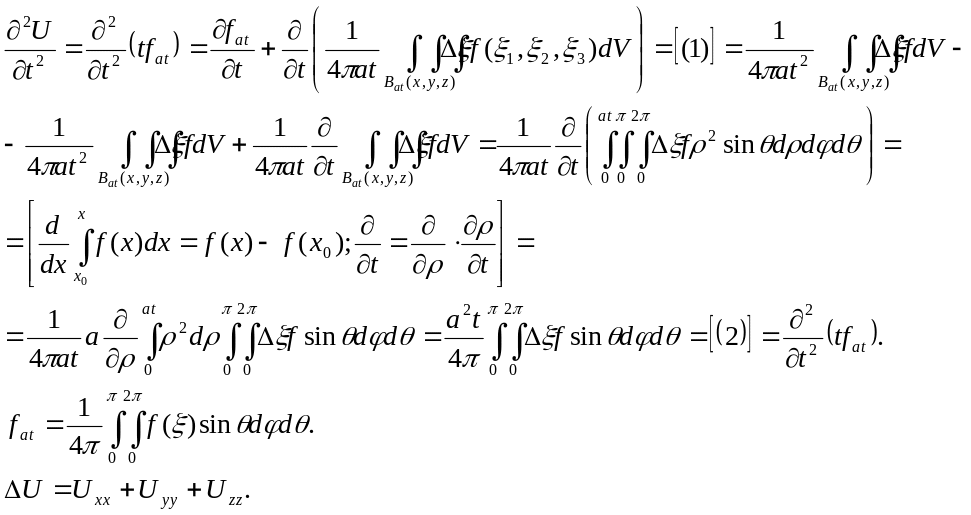
Находим
Умножим на
и сравним с (2), получим доказательство
Леммы. Покажем, что функция
является решением этого уравнения
Задача Коши для трехмерного волнового уравнения.
(1)
Решение этой задачи – сумма решений двух задач:
(2)
(3)
Решение задачи (2) определяется формулой Кирхгофа.
где
По предыдущей лемме функции
являются решениями трехмерного
однородного волнового уравнения. По
свойству решений линейного уравнения
сумма любых его решений - так же решение.
А это означает, что функция
решение уравнения задачи (2).
Покажем, что
удовлетворяет и начальным условиям
задачи (2).
Найдем
Для решения задачи
(3) воспользуемся принципом Дюамеля,
согласно которому, если функция
является решением вспомогательной
задачи
(4),
то функция
(5)
является решение задачи (3).
Действительно,
так как
решение задачи (4), то
Подставим функцию
(5) в уравнение (3)
Найдем функцию
или решение задачи (4). Для этого сделаем
замену
Придем к задаче
Последняя задача
является задачей Коши для трехмерного
однородного волнового уравнения, а
значит решение этой задачи определяется
формулой Кирхгофа.
решение
задачи (3).
Задача Коши для двумерного волнового уравнения.
(1)
Решение этой задачи можно привести, используя формулу Кирхгофа и принцип Дюамеля, но так как в двумерном случае пространственных переменных только две, то вычисления средних значений функции на сфере можно упростить, сведя их к вычислению интегралов по площади круга.
Уравнение нашей сферы в трехмерном пространстве имеет вид:
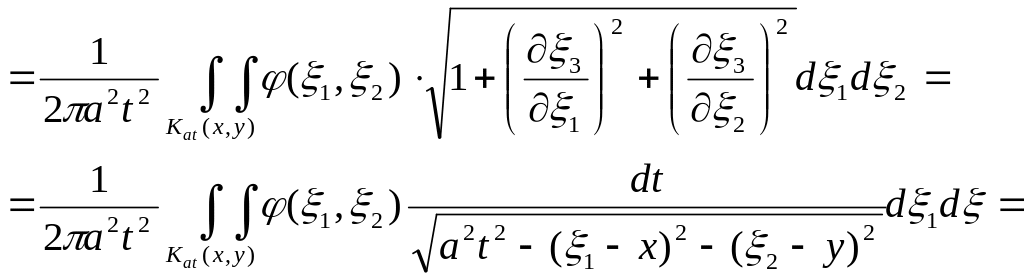
(2)
Формула Кирхгофа, в которой среднее значение функции вычисляются по формуле (2) носит название Пуассона.
Некоторые методы решения Задачи Коши.
Рассмотрим пример № 1:
,
Будем искать
решение такого уравнения
Следовательно
.
Общее решение
,
,
Пример № 2:
решение
Для решения этой задачи:
можно пользоваться не только формулой Кирхгофа, но применять другие методы решения.
,
k- число
,
,
задача Коши
Пример № 3:
многочлены
Пример № 4:
Пример № 5:
Теперь решаем задачу:
Раскрываем скобки, приводим подобные и получаем:
A=0
.
Следовательно
