Уравнение колебаний мембраны.

Под мембраной будем понимать свободно изгибающуюся натянутую пленку.

Предположим, что в положении равновесия мембрана расположена в плоскости занимает некоторую область и ограничена замкнутой кривой Будем рассматривать только малые поперечные колебания мембраны, причем все точки мембраны движется параллельно оси , которая перпендикулярна плоскости

Выделим произвольный участок мембраны ограниченный в положении равновесия контуром После деформации этот участок переходит в часть поверхности

Найдем площадь поверхности

Это означает, что в процессе малых колебаний изменения площади выделенного участка пленки не происходит. В силу закона Гука последнее означает, что к контуру приложена постоянная сила натяжения.

Обозначим через величину внешней силы, приложенной в момент времени в точке с координатами

Найдем сумму проекций на ось сил, приложенных к контуру участка мембраны.

Обозначим через элемент дуги кривой и через силу натяжения, приложенной в каждой точке этого элемента. Тогда величина, приложенная ко всему элементу, обозначается

Нужно учесть, что вектор, направление которого перпендикулярно направлению касательной к середине элемента и нормали к поверхности в этой же точке.

Таким образом, вектор нормали к поверхности, заданный уравнением определяется направляющими косинусами.

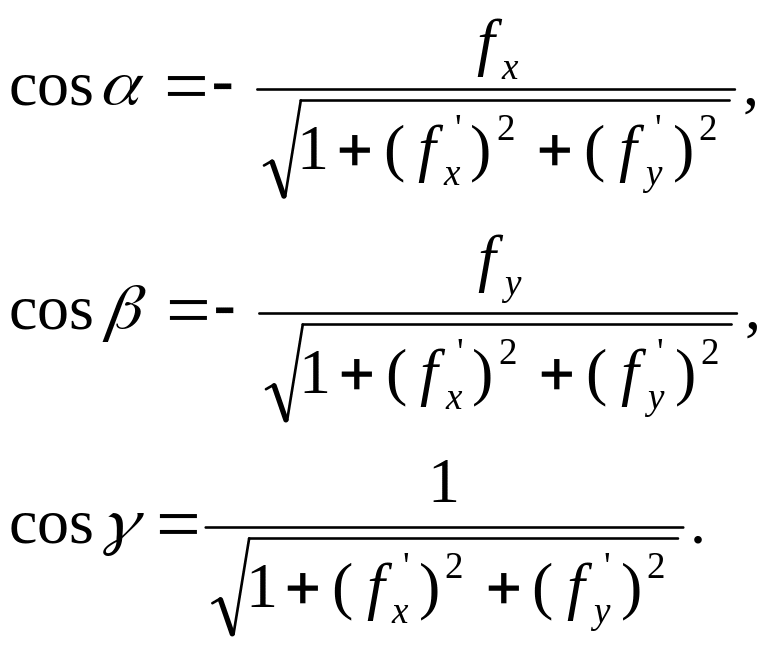
В нашем случае в роли функции в каждый фиксированный момент времени выступает функция и, следовательно, в силу малости колебаний будет иметь координаты

Вектор касательной может быть представлен в виде:

Тогда вектор

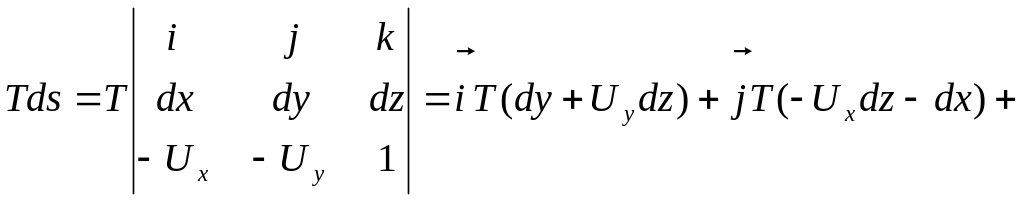
Сумма проекций равнодействующей силы натяжения, приложенной ко всему контуру равна:

Сумма проекций всех внешних сил, действующих на участке мембраны:

Обозначим, через поверхностную плотность пленки, тогда масса элемента равна:

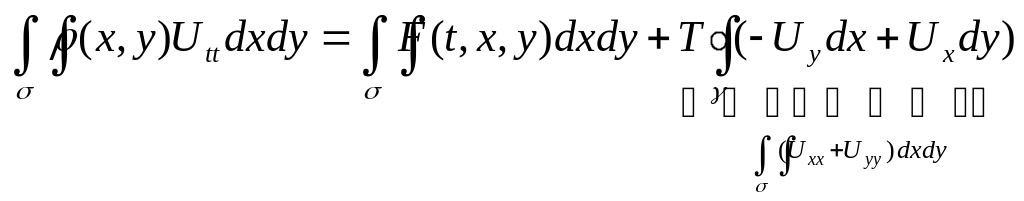
формула Грина.

Если пленка однородная, то разделим на , получим:

двумерное волновое уравнение.

Заметим, что при выводе уравнения мы считаем силу натяжения постоянной, не зависящей от времени и координаты точки.

Если сила натяжения зависит от координаты точки, то уравнение примет вид:

Задачи, приводящие к трехмерному волновому уравнению.

1. Схема вывода уравнения колебаний электромагнитного поля.

Основными характеристиками электромагнитного поля является два вектора: вектор напряженности электромагнитного поля,

вектор электромагнитной индукции.

Напомним, что

Вектора направленности и вектор магнитной индукции в вакууме связаны с уравнениями Максвелла:

Продифференцируем последнее уравнение из системы уравнений Максвелла по , получим:

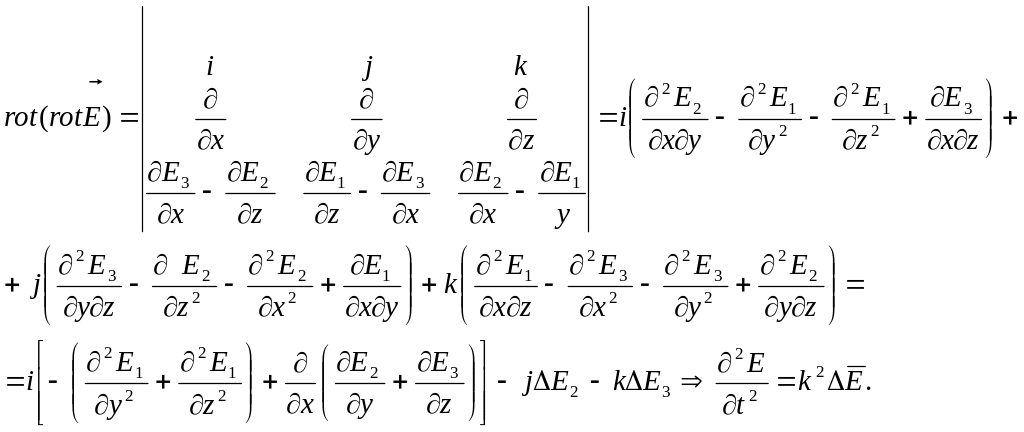
Таким образом, получим уравнение, описывающее колебания напряженного трехмерного электромагнитного поля. Аналогичным образом может быть получено уравнение, описывающее колебания вектора магнитной индукции:

С использованием уравнений гидродинамики можем получить уравнение акустики (уравнение распределения звуковых волн). Все предыдущие примеры приводили нас к волновым уравнениям. При этом эти уравнения оказывались линейными. При других предположениях может оказаться, что волновой процесс описывается не линейным уравнением (мы не рассматриваем).