Телеграфные уравнения.
Будем рассматривать
двухпроводную линию, напряжение и ток
которой зависят от координат точки этой
линии и времени:
напряжение,
сила
тока. Пусть
активное
сопротивление,
емкость,
индуктивность.
Буквой
обозначим активную проводимость между
проводами.
Разность напряжений
в начале и в конце рассматриваемого
участка длиной
равна
сумме падения напряжений на активном
сопротивлении
и индуктивного падения напряжения
отсюда:
(1)
Изменение силы
тока на рассматриваемом участке
обусловлено током утечки, который равен
и током смещения
(2)
(1) уравнение
продифференцируем по
а (2) по
Следовательно,
(1’),
(2’).
Из (2’)
найдем
из (2) найдем
(3)
Уравнение (3) – телеграфное уравнение.
Это уравнение описывает процесс изменения напряжения двухпроводной линии. Аналогичным образом получаем уравнение, описывающее колебание тока в двухпроводной линии.
(3’)
Предположим, что линия имеет бесконечную длину, это означает, что граничные условия не оказывают существенного влияния, а поэтому остановимся только на получении начальных условий.
Из уравнения (2)
Рассмотрим некоторые частные случаи телеграфного уравнения:
Линия без потерь.
Такой линией считаем линию, у которой
активное сопротивление
и
где
Введем
Легко найти закон изменения напряжения
в линии без потерь. В этом случае задача
принимает вид:
две
характеристики.
Подставим в
уравнение
:
канонич.вид.
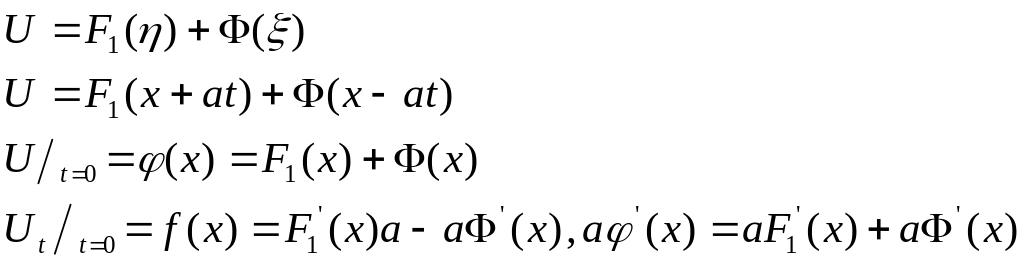
Полученная формула
носит название формулы
Даламбера
решения задачи Коши для одномерного
волнового уравнения. Учтем, что в нашем
случае:
Тогда получим:
Линия без искажений.
(3)
1)
2)
линия
без искажений.
Покажем, что в этом случае процесс колебания тока и напряжения описывается той же формулой (что и в случае линии без потерь, но с постоянно уменьшающейся амплитудой).
В уравнении (3)
сделаем замену:
,
или
Это уравнение совпадает с уравнением, описывающем изменение напряжения в линии без потерь, а, следовательно, его решение будет определяться той же формулой:
Таким образом, амплитуда колебаний уменьшается со временем.
Линия конечной длины.
В реальной жизни линий бесконечной длины не бывает и если линия имеет конечную длину, то на концах этой линии можно задать граничные условия. Приведем примеры граничных условий:
______________
______________
x=0 x=l
Если на каком –то конце линии включен источник тока с некоторой электродвижущей силой, то граничные условия принимают вид:
В случае короткого
замыкания на каком – то из концов
граничное условие примет вид:
В случае наличия
в сети переменного напряжения
Если конец линии
изолирован, то это означает, что сила
тока на этом конце равна нулю:
Если на конце линии
имеется потребитель энергии, сопротивление
которого R,
а индуктивность L,
то
