Свойства потенциалов двойного слоя.

В дальнейшем нам понадобится понятие поверхности Ляпунова. Замкнутую поверхность будем называть поверхностью Ляпунова, если выполняются следующие условия:

1) В каждой точке поверхности существует касательная плоскость. Это позволяет в каждой точке поверхности построить местную или локальную систему координат, ось которой направлена по внешней нормали поверхности.

2) В этой системе координат часть поверхности, заключено внутри шара с центром в начале координат и достаточно малого радиуса имеет уравнение: причем частные производные являются непрерывными функциями. Можно показать, что если ограниченная замкнутая поверхность Ляпунова, то существует постоянная

Теорема 1. Вне точек несущей поверхности потенциал двойного слоя является функцией гармонической

Доказательство:

◄

Покажем, что при Для этого внутри поверхности выберем точку

Обозначим через наибольшее расстояние между точками и и выберем точку настолько удаленной от точки чтобы то есть

►

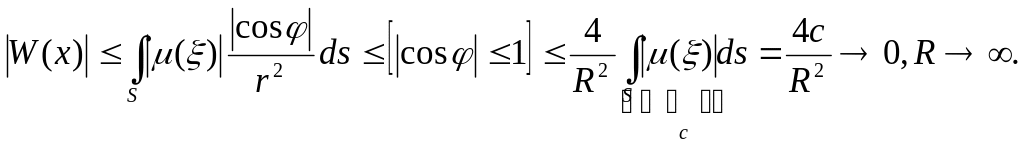Теорема 2. Потенциал двойного слоя определен всюду.

Доказательство: ◄

Если точка не принадлежит несущей поверхности, то потенциал двойного слоя представляет собой собственный интеграл. Следовательно, вне точек несущей поверхности он определен .

Пусть точка принадлежит несущей поверхности , тогда .

В этом случае имеем несобственный интеграл. Для того, чтобы потенциал двойного слоя был определен в точках несущей поверхности, нужно исследовать его сходимость в окрестности точки . В точке построим местную систему координат. Уравнение куска поверхности, заключенного внутри сферы малого радиуса записывается: Обозначим кусок поверхности, вырезанного из сферы малого радиуса через получим

Следовательно, потенциал двойного слоя определен всюду, в том числе и в точках несущей поверхности. ►

Если т. лежит вне несущей поверхности и приближается к. поверхности. Если существует предел потенциала двойного слоя, то говорят, что в т. поверхности потенциал двойного слоя принимает предельное значение. Это предельное значение различно и зависит от того, изнутри или из вне поверхности находится т. . Рассмотрим потенциал двойного слоя с единичной плотностью: Можно показать, что этот потенциал равен: .

Интеграл называется интегралом Гаусса. Очевидно, что этот интеграл терпит разрыв, когда с т. пересекает поверхность .

Пусть т. находится вне замкнутой поверхности , то т.к. является гармонической функцией вне поверхности , то согласно интегральной теореме Гаусса:

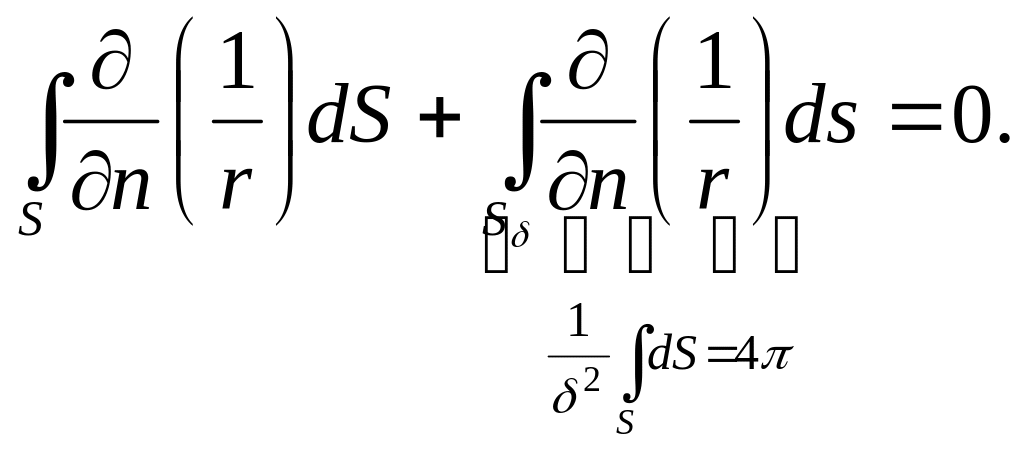
Рассмотрим теперь: т. находится внутри замкнутой поверхности Окружим ее сферой радиуса и обозначим ее .Область между и обозначим через Функция является гармонической в области По интегральной теореме Гаусса: т.к.

Используя местную систему координат можно показать, что если т. на . С использованием интеграла Гаусса доказывается следующее утверждение: Теорема: Потенциал двойного слоя имеет пределы при стремлении т. к т. , несущей поверхности изнутри и извне. Если обозначить предел и из вне, предел изнутри, то

Потенциал простого слоя.

Потенциалом простого слоя называется потенциал, создаваемый зарядом с плотностью , расположенными на поверхности и

Легко показать, что вне несущей поверхности потенциал простого слоя является функцией гармонической: .

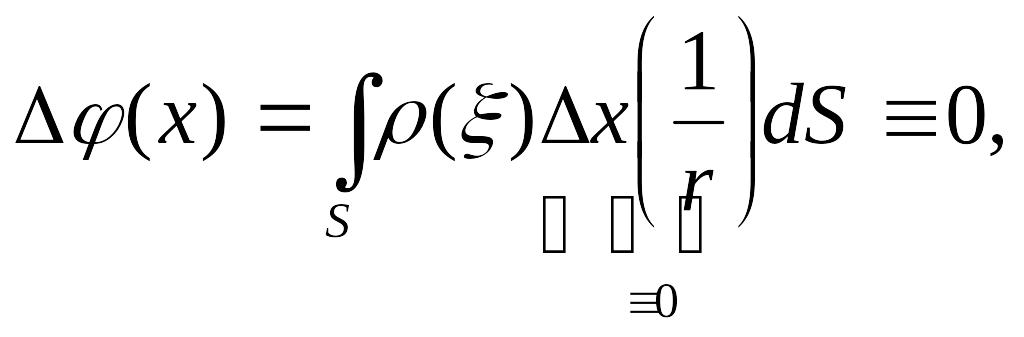
при

Пусть произвольная точка поверхности лежащая на этой поверхности т. -примем за начало системы координат, то т. в этой системе координат имеет координату т. .

Обозначим через наибольшее расстояние между т. и т. .Выберем т. настолько отдаленной от т. , что бы выполнилось неравенство .По неравенству треугольника:

То где

Если то т.е. выполняется условие на бесконечности. Производная по нормали потенциала простого слоя:

Это производная, т.е. производная по нормали, напоминает потенциал двойного слоя зависит от несущей т. несущей поверхности, по которой ведется интегрирование. В нашем случае является фиксированным значением, т.к. нормаль вычисляется в фиксированной т. Справедлива следующая теорема : Теорема: Потенциал простого слоя имеет производные по нормали на несущей поверхности изнутри и извне. Причем

,

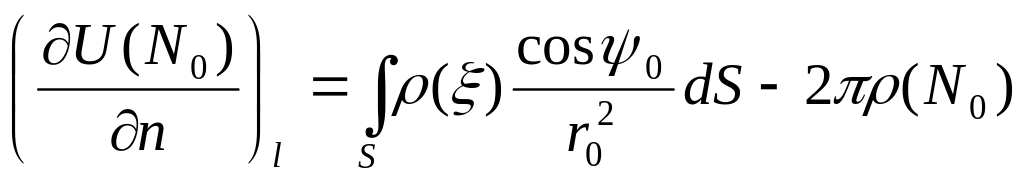а : Теорема:лоя 00000000000000000000000000000000000000000000000000000000000000000000000000000000000й системе ло координат т.и потенциал простого слоя является функцией г00000000000000000000000000000000000000000000000000000

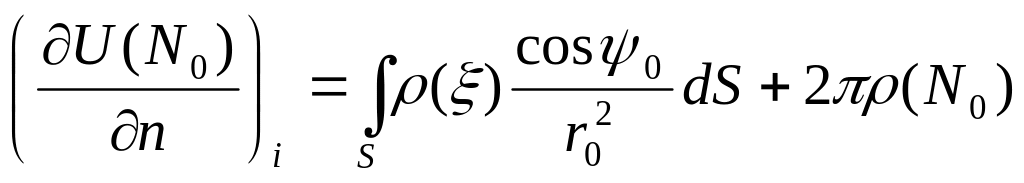
Сведения краевых задач к интегральным уравнениям.

Пусть замкнутая поверхность Ляпунова и имеет задачу Дирихле

о найдем п00000000000000000000000000000000000000000000000000000000000000000000000000000000

.

Будем искать решение задачи Дирихле в виде потенциала двойного слоя:

с неизвестной пока плотностью распределения диполей

Подберем плотность таким образом, чтобы значение потенциала двойного слоя изнутри совпадало в точке со значением функции

В случае внешней задачи Дирихле неизвестная плотность определяется из уравнения:

Пусть теперь имеем задачу Неймана для уравнения Лапласа:

Решение этой задачи будем искать в виде потенциала простого слоя

с неизвестной плотностью распределение заряда по поверхности. Для решения внутренней задачи для определения неизвестной плотности получим уравнение: для внешней задачи: Таким образом, решение краевых задач свелось к решению интегральных уравнений с последующим отысканием поверхностных интегралов.

72