Теория потенциалов Объемный потенциал, потенциал простого слоя, потенциал двойного слоя.

Пусть в т. помещён заряд , то этот заряд создаёт электростатическое поле, напряжённость которого в т. определяется.

,

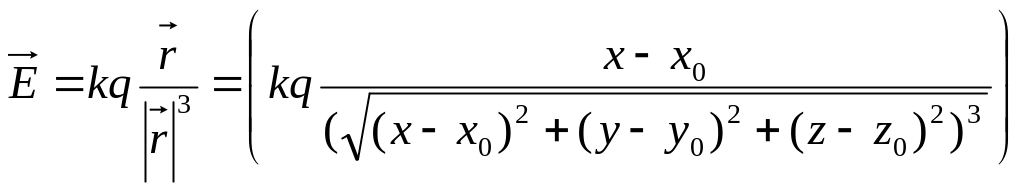Коэффициент зависит от выбранной системы единиц в дальнейшем будем считать .

Легко видеть, что компоненты вектора равны в противоположным знаком противоположной от функции .

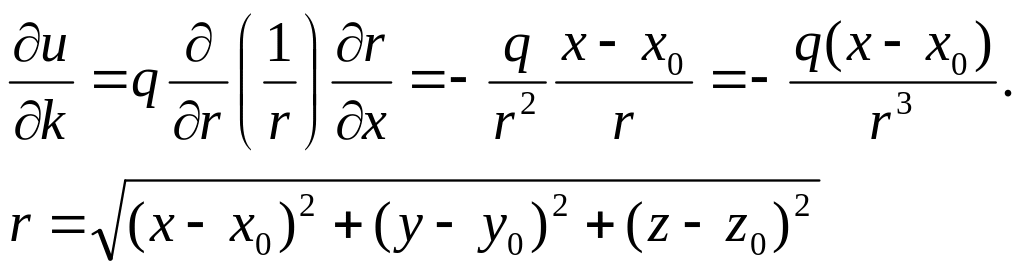
Функцию называют потенциалом электростатического поля. Т.к. при наличии нескольких зарядов потенциалы складываются то потенциалы, создаваемые непрерывно распределяющими зарядами будут находиться в виде интеграла. Предположим, что заряд распределён по объему с объёмной плотностью . То потенциал, создаваемый зарядом, распределённым по объёму, будет определяться формулой:

Правая часть последнего выражения называется потенциалом объёма. Пусть заряд распределен по поверхности с поверхностной плотностью, следовательно, потенциал, создаваемый этим зарядом определяется формулой:

U- называется потенциалом простого слоя.

Пусть дана ориентированная прямая и на ней т. . По разные стороны от этой точки находятся заряды и , расстояние между которыми . Возьмём т. , лежащую вне этой прямой, следовательно, потенциал

Пусть эти заряды приближаются к т.А, причем каждый из них остается на своей стороне от т.А .

Предположим, что в процессе движения, величина заряда меняется таким образом, что

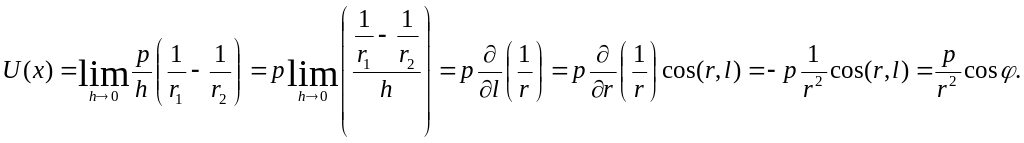
Рассмотрим теперь ориентированную поверхность .Предположим, что на этой поверхности распределен заряд с момента диполя Заметим, что величина P-момент диполя, l –ось диполя, а диполем называется предельное положение зарядов противоположных знаков, то потенциал, создаваемый этим зарядом равен:

здесь угол между и - внешняя нормаль к поверхности.

Выражение называется потенциалом двойного слоя. Заметим, что в подынтегральных выражениях всех потенциалов присутствует множитель , который не равен нулю, если точка, в которой распределяется потенциал, лежит вне области распределения зарядов и обращается в бесконечность, если т.M и N лежат в области распределения зарядов.

Несобственный интеграл, зависящий от параметра.

Известно, что если подынтегральная функция в обращается в бесконечность в некоторой точке области , то интеграл нельзя определить как предел интегральной суммы.

Рассмотрим определенный интеграл по области где окрестность точки x, в которой подынтегральная функция обращается в бесконечность. Понятно, что является собственным.

Пусть Если существует конечный предел при

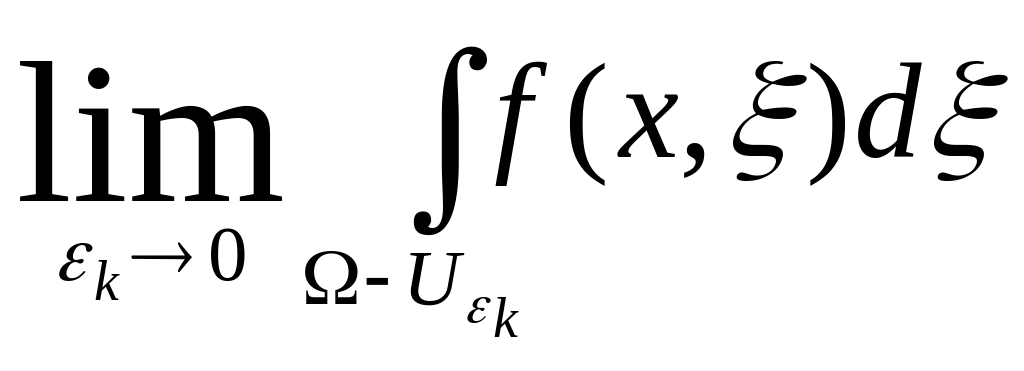, то называется несобственным интегралом, зависящим от параметра. Если где то несобственный интеграл сходится при если , а при если .

Свойства объемного потенциала.

Рассмотрим объемный потенциал:

U(x)=

Теорема1: Если плотность ограничена и интегрируема в области , то объемный потенциал является функцией, гармонической вне этой области.

Доказательство:

Т.к. точка M лежит вне области , то объемный потенциал является собственным интегралом, т.к. -непрерывна и имеет непрерывные производные всех порядков, которые могут быть найдены дифференцированием под знаком интеграла.

удовлетворяет уравнению Лапласа.

Для оценки последнего интеграла поместим начало координат внутри области Пусть d-диаметр области Выберем M настолько удаленную от начала координат, чтобы

Теорема2: Если ограничена и интегрируема в области потенциал и его частные производные первого порядка определены во всем пространстве U и эти производные могут быть найдены дифференцированием под знаком интеграла.

Доказательство:

◄ Для доказательства достаточно показать, что .Определены через несобственные интегралы, которые равномерно сходятся в любой точке M области называется равномерно сходящимся в т.M, если: : расстояние, которое и для области , диаметр которой

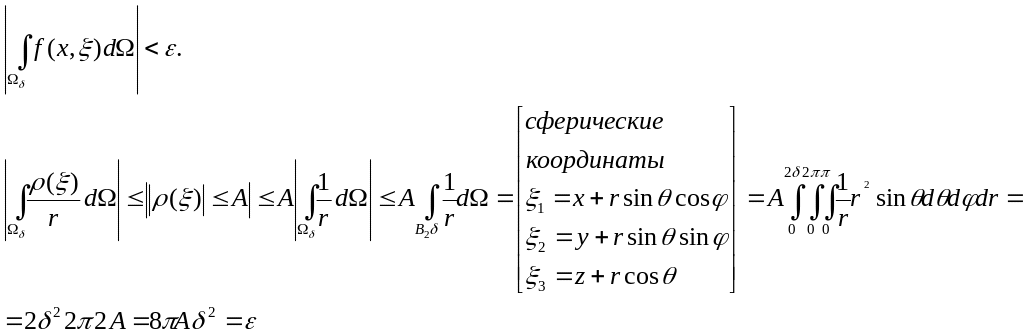
-равномерная сходимость доказана.

Аналогично,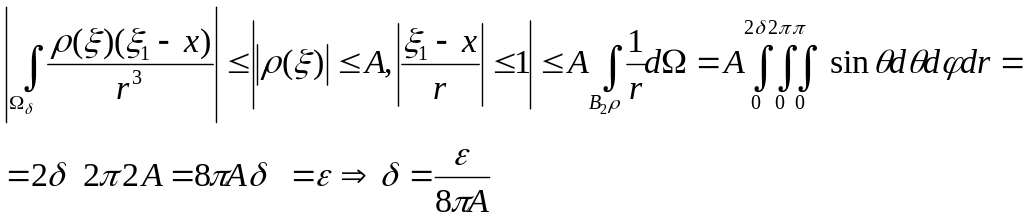

Остается показать, что Пусть

Покажем:

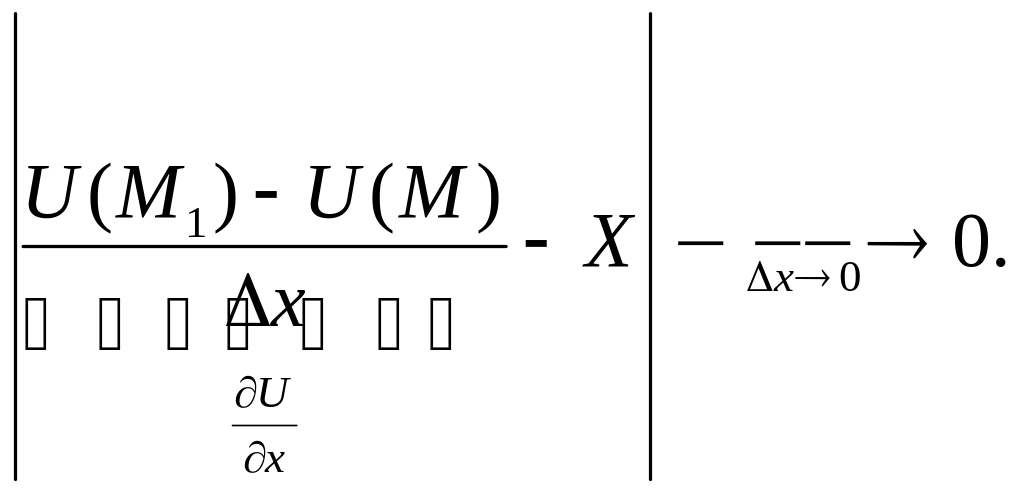
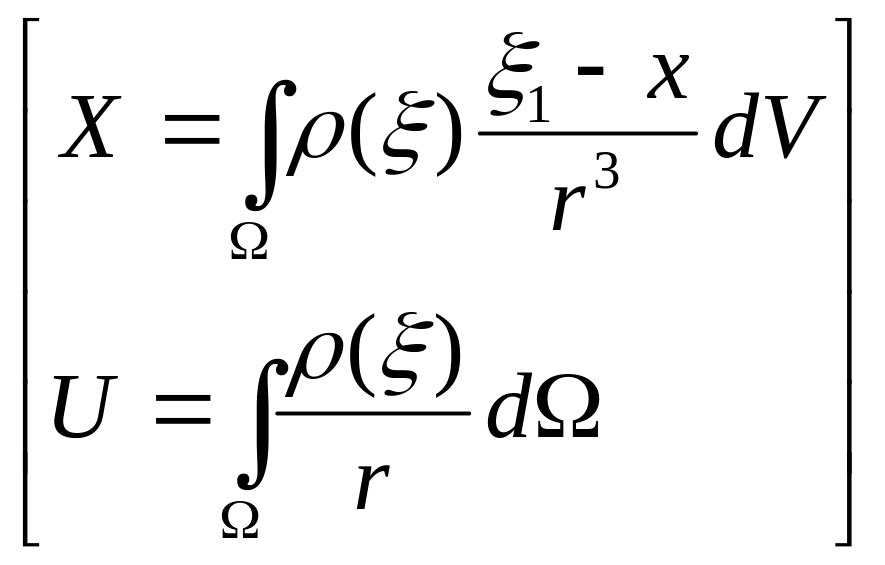
В области возьмем шар, радиуса ,т.е. , содержащий т.М, то через

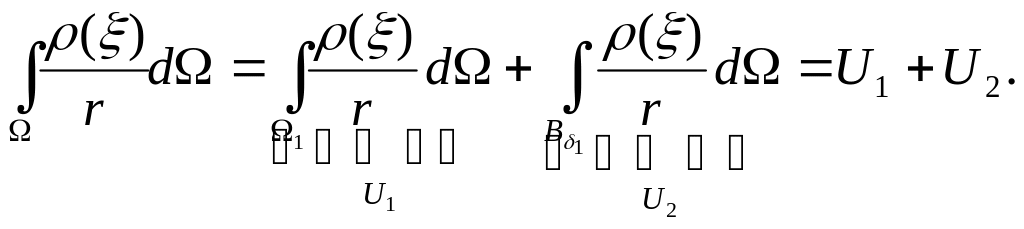
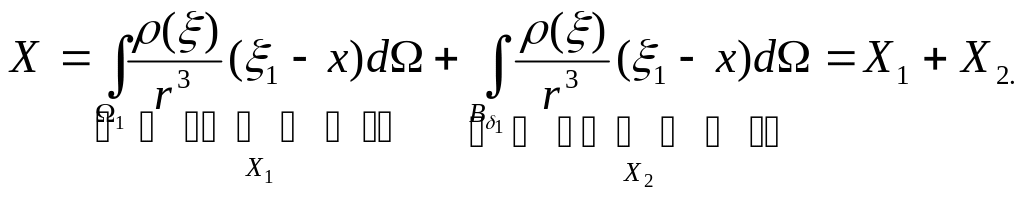
. Первое слагаемое представляет собой разность между производной функцией и X.

Рассмотрим второе слагаемое. Для этого найдем предварительно оценку:

. ►

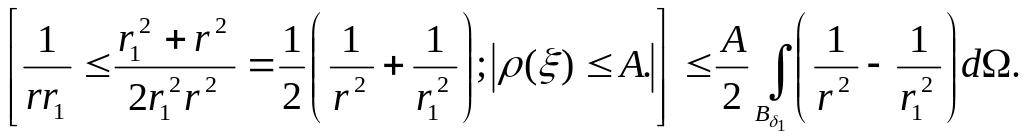
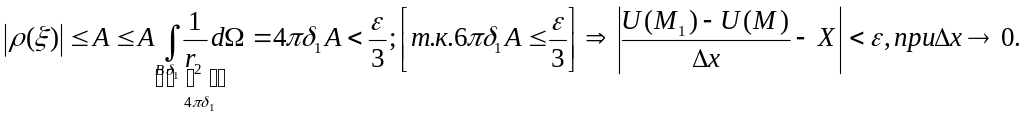
Теорема3: (без доказательства)Если непрерывна в и имеет непрерывные в производные первого порядка , то объемный потенциал имеет непрерывные в производные второго порядка и удовлетворяет уравнению Пуассона: