Неравенство Харнака. Теорема Лиувилля.
Пусть функция
-гармоническая
внутри круга и не отрицательная
.
Согласно неравенству треугольника
задача Дирихле:
Умножим неравенство
на
и проинтегрируем по поверхности, радиуса
R
.
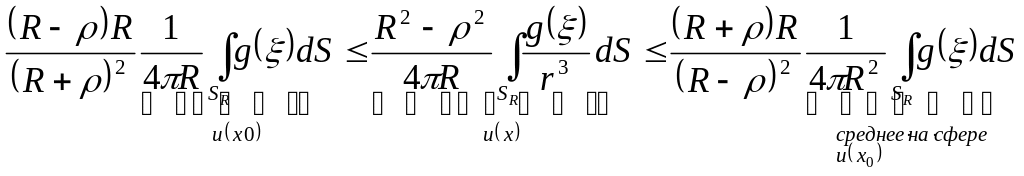Следовательно,
-
неравенство Харнака.
-
значение функции в центре шара.
Из неравенства Харнака легко получить теорему Лиувилля.
Теорема: Если функция - гармонична во всём пространстве и ограничена сверху или снизу, то она постоянна (тождественна 0).
Доказательство: ◄
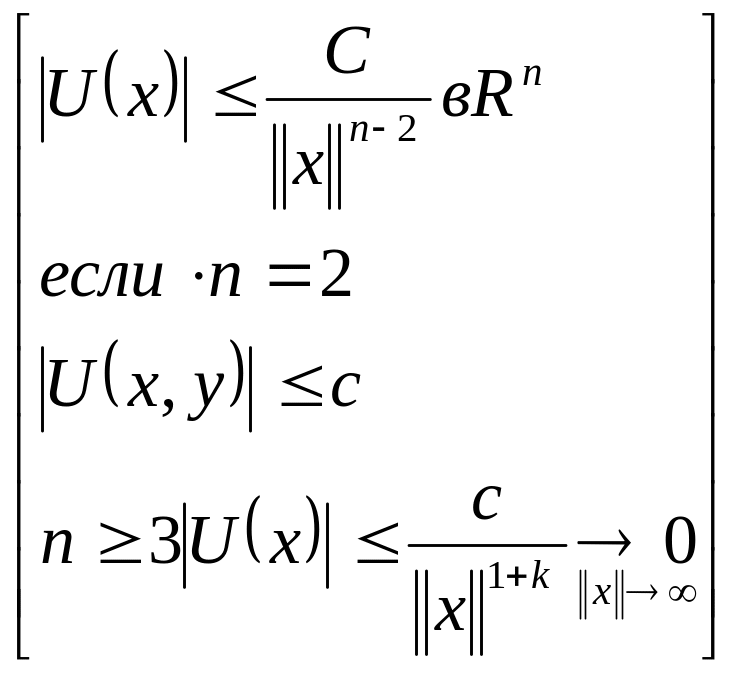Т.к.
функция гармонична во всём пространстве,
то она гармонична и в шаре, радиуса
,
.
Обозначим
.
функция
и является гармоничной в шаре радиусом
и
справедлива неравенство Харнака.
.
при
, 
-
постоянная.
Заметим, что в
случае
постоянная
является функцией гармонической в
неограниченной области (а в случае
постоянная
может быть гармонической функцией в
неограниченной области, если она равна
0). ч.т.д. ►
Поведение произвольных гармонических функций на бесконечности.
Легко показать,
что решение внешний задачи Дирихле для
шара определяется формулой:
.
Действительно,
найдём
:
.
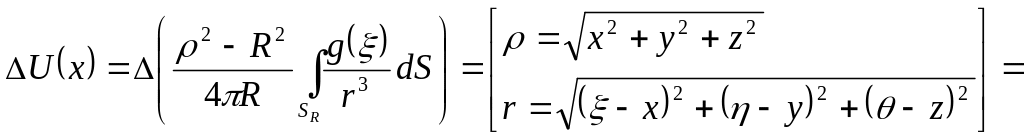
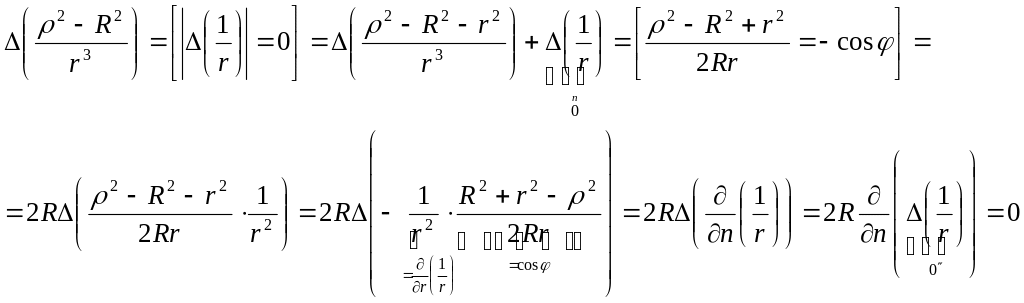
Покажем, что
при
. 
т. М
возьмём так далеко от центра шара, чтобы
т.е.
в силу неравенства
,
;
,
.
,
где
.
.
.
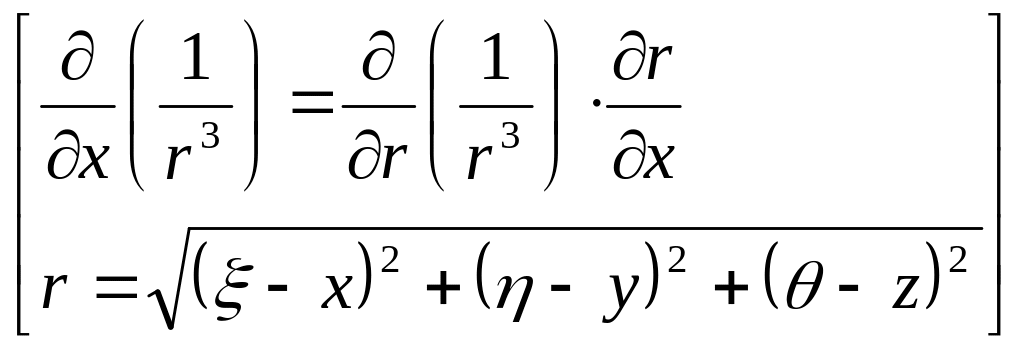. Учитывая,
что
,
для
. Следовательно,
где
.
Аналогично,
находятся оценки
и
.
Теорема единственности решения задачи Неймана.
При обосновании этой теоремы нам понадобится первая формула Грина и понятие регулярной поверхности или поверхности Ляпунова.
Для оператора
- мы получим 1-ю формулу Грина:
Если
в
этой формуле
Тогда формула принимает вид:
первая
формула Грина для оператора Лапласа.
Поверхность Г называется регулярной, если:
в каждой точке поверхности существует определенная нормаль
если в каждой точке поверхности выбрать местную систему координат, ось z которой направить по нормали, то в этой системе координат уравнение части поверхности Г , находится в окрестности начала этой системы координат запишется в виде уравнения:
причем f
-дважды непрерывно дифференцируемая.
Теорема: Если Г регулярная поверхность, ограничивающая поверхность , то решение внутренней задачи Неймана определено с точностью до постоянной, а внешней задачи единственно.
Доказательство:
Допустим решение
внутренней задачи не единственно. Пусть
и
-два различных решения этой задачи.
Обозначим
, где
решение
этой задачи.
Первую формулу
Грина перепишем, полагая
Т.к. V-гармоническая
внутри
,
Если
и
производная по каждой переменной
равняется нулю
.
Будем считать, что
имеем внешнюю задачу Неймана с конечной
регулярной границей
.
Предположив существование двух различных
решений внешней задачи Неймана и
обозначив разность этих решений через
как и в случае внутренней задачи для
функции
получим задачу Неймана для уравнения
Лапласа с нулевым ограниченным условием.
Для неограниченной области первая
формула Грина неприменима, т.к. граница
- конечная, то её можно заключить внутри
сферы достаточно большого радиуса.
Область, заключённая
между
и
являются ограниченной и для этой области
формула Грина примет вид:
,
Т.к.
функция гармоническая в неограниченной
области, то для этой функции и ее
производных справедливы оценки:
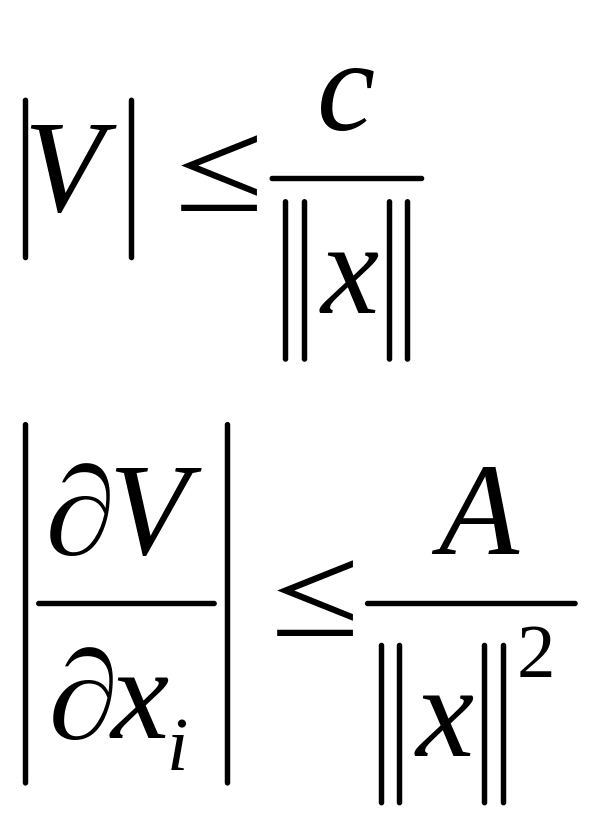
Функция является гармонической в неограниченной области
при
