Формулы Грина. Интегральная теорема Гаусса.
При изучении
решения смешанных задач мы ввели в
рассмотрение линейный оператор:
При доказательстве самосопряженности этого оператора была получена первая формула Грина:
Меняя местами функции и запишем еще одну формулу:
- вторая формула
Грина.
Заметим, что вторая формула Грина справедлива и для областей, ограниченных несколькими поверхностями.
Если
Здесь положим
а
будем считать гармонической в ограниченной
области
получим:
суть
интегральной теоремы Гаусса.
Если
гармоническая
в ограниченной области
с границей
функция, то интеграл по границе от
производной по нормали этой функции
равен нулю. Интегральная теорема Гаусса
дает необходимое условие существования
решения внутренней задачи Неймана:
Интегральное представление произвольной функции.
Теорема:
Если
непрерывна
в
и имеет непрерывные вплоть до границы
производные первого порядка и непрерывные в производные второго
порядка,
то
-
площадь поверхности сферы Римана
единичного радиуса n-го
пространства.
Известно, что
функция Еn
является
гармонической везде исключая т.
где она обращается в бесконечность.
Вспомним вторую формулу Грина: 
.
Вторая формула Грина справедлива и для случая области, граница которой является объединением некоторых границ (множеств). В области вырежем шар, радиусом с центром в т.
Область, заключённую
между
и
объемом
и запишем вторую формулу Грина для этой
области, положив
Получим:
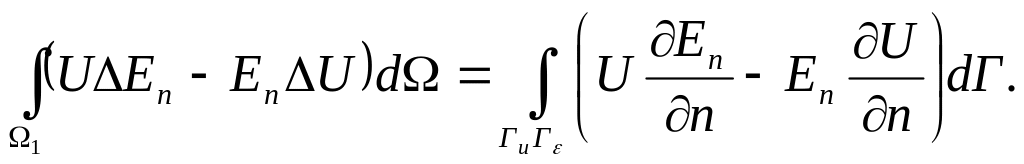
Заметим:
Т.к. En
– гармоническая в
, то
Получаем:
(*) 
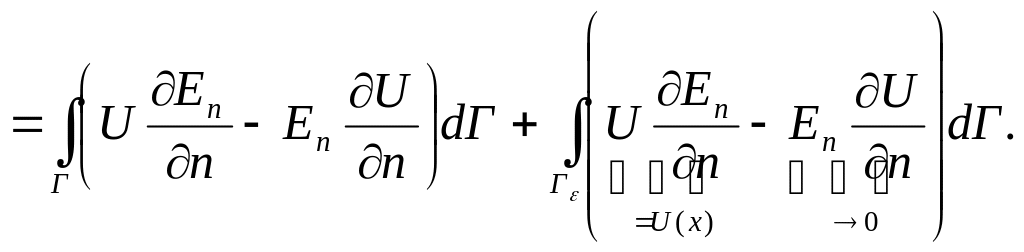
=(если
)=
Рассмотрим интеграл
и найдём его значение из, и
Для этого
=
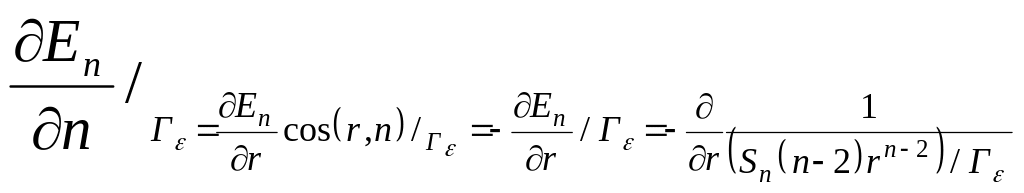площадь поверхности сферы радиуса в n- мерном пространстве
Находим
- фиксируемая точка сферы
Рассмотрим теперь 
; 
Продолжая
получим: 
Заметим, что если
- гармоническая, то
,
т.к
Теорема об аналитичности гармонической функции: Функция гармоническая в по кривой имеет в этой области производные всех порядков.
Доказательство:
◄ В области
возьмём
произвольную т.
поверхности
, целиком лежащая в
т.к. функция
гармоническая в
,
то она является гармонической и в обл.
ограниченной
причём в области
функция
имеет
производные 2-го порядка непрерывные.
Согласно интегральному
представлению функции гармонической
в
получаем:
; 
; 
Во втором интеграле
т.
не лежит на поверхности
производные по
и
существуют, причём любого порядка. Т.
обр. функция
имеет производные любого порядка,
которые можно найти дифференцированием
под знаком интеграла.
►.
Теорема о среднем на сфере
Теорема: Среднее значение на сфере гармонической в шаре = значению этой функции в центре шара.
Доказательство:
◄
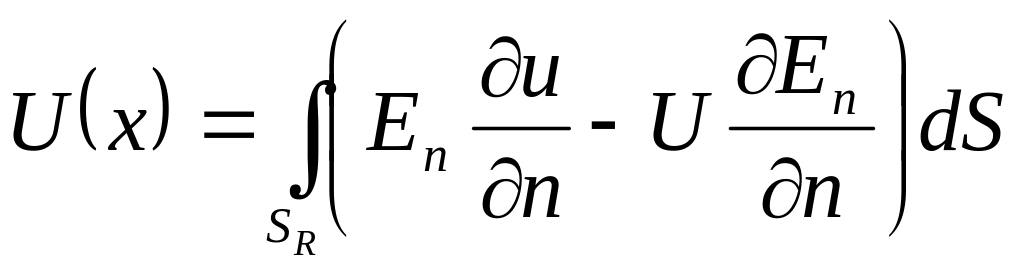
Пусть
-
центр шара
►
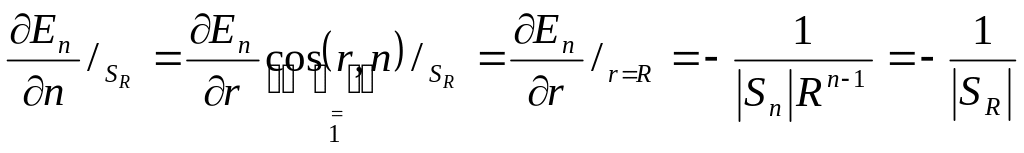