Решение задачи Дирихле для уравнения Лапласа в круге и вне круга.

Рассмотрим задачу:

Найдём решение внутренней задачи Дирихле для круга.

Задача преобразуется к виду:

Разложим функцию в ряд по функциям но sin, cos кратных дуг.

где

,

Естественно, решение внутренней задачи Дирихле искать в виде ряда:

U

Эта функция будет гармонической внутри круга, если положить

Т.к. на границе круга решение должно совпадать с :

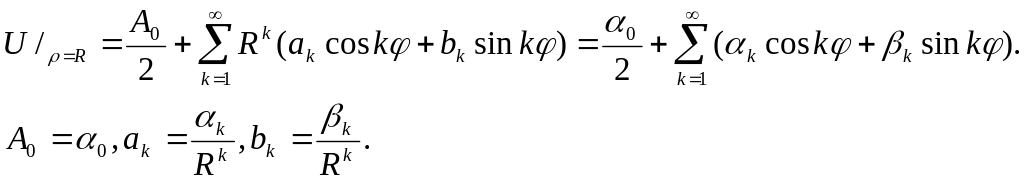
Т.обр. решение внутренней задачи представляется в виде ряда:

Решение внешней задачи Дирихле определяется рядом:

Найдем сумму ряда, представляющего решение внутренней задачи Дирихле.

Подставим в ряд

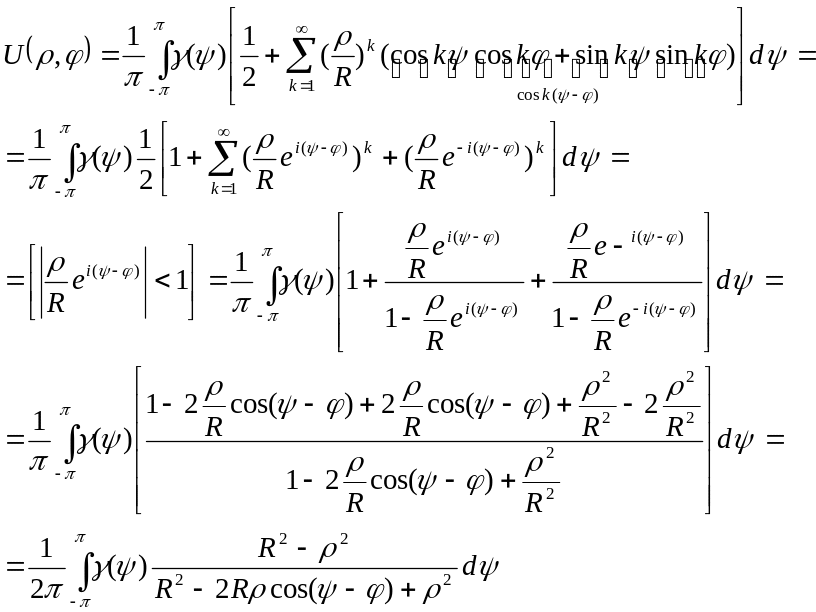
Т.обр. решение внутренней задачи Дирихле определяется формулой:

-формула Пуассона решения внутренней задачи Дирихле для круга.

В случае внешней задачи перед знаком интеграла будет знак минус.

Решение внутренней и внешней задачи Неймана для круга.

Рассмотрим задание:

, где и определяется по функциям предыдущего пункта

Решение задачи Неймана будем искать в виде: .

Для внутренней задачи: .

Для внешней задачи:

Найдём для внутренней задачи

.

Последние ряды должны совпадать с рядом для . Последние будет выполнятся, если , - для внутренней задачи

, - для внешней задачи

Т.к. в рядах, представляющих значение производных по нормам от решений задачи Неймана отсутствует свободный член, то для существования решения этих задач должно выполняется условие.

Решение задачи Неймана заключается:

- внутренняя задача

- внешняя задача

Из вида этих решений что решение задачи Неймана определено с точностью до произвольной постоянной.

при

Решение задач Дирихле-Неймана для кольца.

Рассмотрим задачу,

причём сразу перейдём к полярной системе координат:

Среди всех решений уравнения Лапласа выделим те решения, которые представляются в виде:

Подставим в уравнение и получим:

Следовательно, получаем два уравнения:

Тогда получаем, что

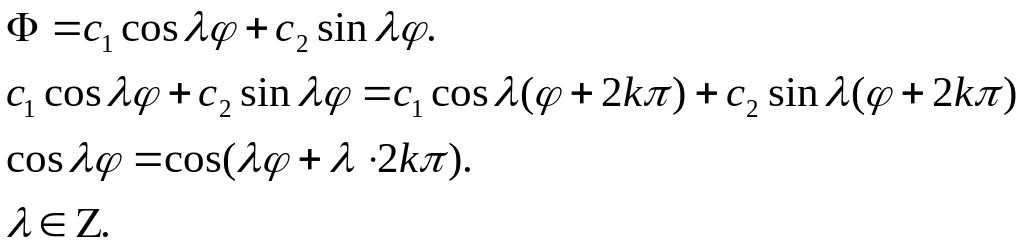
если целое семейство

,

Таким образом, решение можно записать в виде ряда:

(1)

Разложим функции и в ряды:

(2), где

- система для определения и

Подставим в (1)

Аналогично получим систему для определения

Подставляя найденные коэффициенты в ряд (1) получим решение задачи Дирихле для кольца.

Рассмотрим теперь задачу Неймана для кольца

Для её решения воспользуемся рядом (1) считая, что граничные условия определяются рядами (2) и (3).

При получаем:

при этом условие решение задачи 888888888

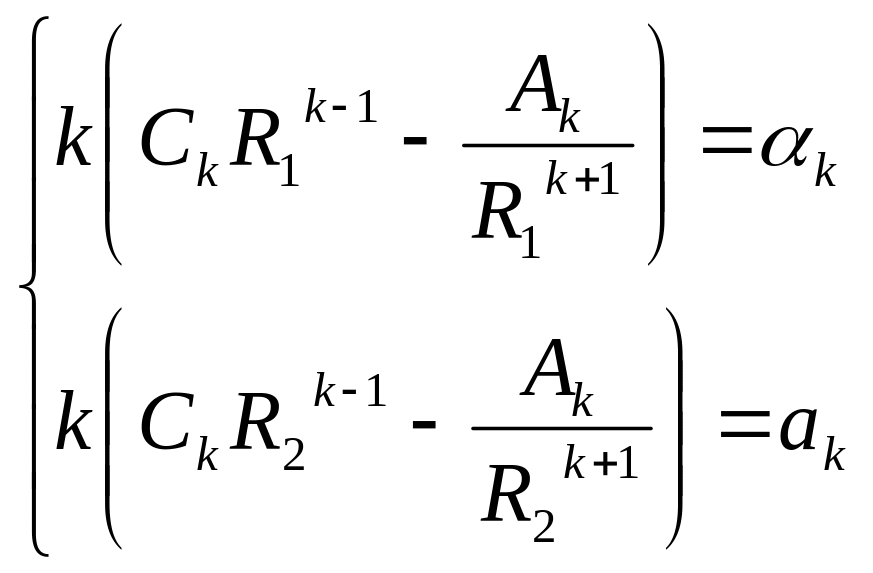- система для определения и

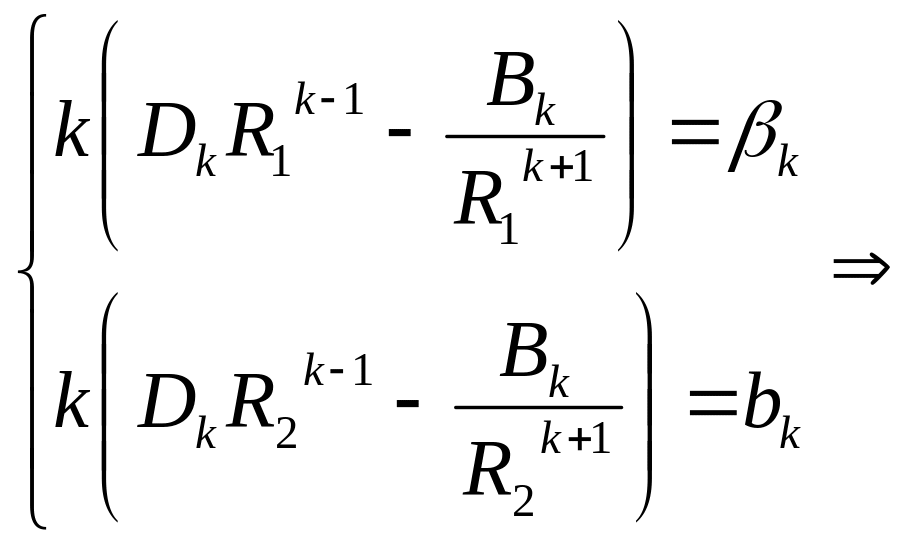решение задачи Неймана заключается в виде ряда (1) с коэффициентами: C₀, A_k, B_k, C_k, D_k, полученными в результате решения последних систем. Но в этом ряде участвует D₀, которое является произвольной постоянной.