Теорема единственности решения смешанной задачи для волновых уравнений.

Существуют различные методы доказательства единственности решения смешанных задач, причём эти методы различны для разных типов задач. Мы будем использовать методику доказательства, основанной на применении первой формулы Грина (эта формула была получении при доказательстве леммы о самосопряженности оператора )

формула Грина.

Рассмотрим задачу (1).

и непрерывны в области (на замкнутом множестве) , непрерывна в области .

Теорема Единственности.

Решение задачи (1) непрерывное в вместе с частичными производными по и единственно.

Док-во.

Предположим противное:

Пусть - два решения задачи (1) непрерывные в вместе с частными производными по и . Обозначим разность этих решений через (т.е. ).

Функция является решение задачи:

(2)

В первой формуле Грина положим .

Получим

(*)

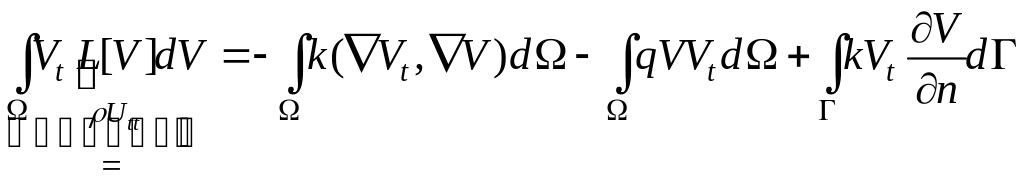После преобразования мы получим следующее уравнение:

Для граничных задач первого типа мы получаем

Для задач второго типа мы получаем:

Для граничных задач третьего типа получаем:

Из формулы (*)

Интегрируя последнее равенство по переменной в пределах от 0 до T, получим:

.

Отсюда следует равенство нулю каждого из интегралов, значит дл первой и второй краевых задач для мы имеем:

Если

Так как

В случае третьей краевой задачи .

Конец доказательства.

Единственность решения смешанной задачи для уравнения теплопроводности.

Рассмотрим задачи (1)

непрерывны на , ,

Теорема:

Решение задачи (1) непрерывно в области вместе с частными производными по и единственно.

Доказательство.

Пусть - 2 различных решения задачи (1).

- решение задачи (2)

(2)

В первой формуле Грина положим . Тогда

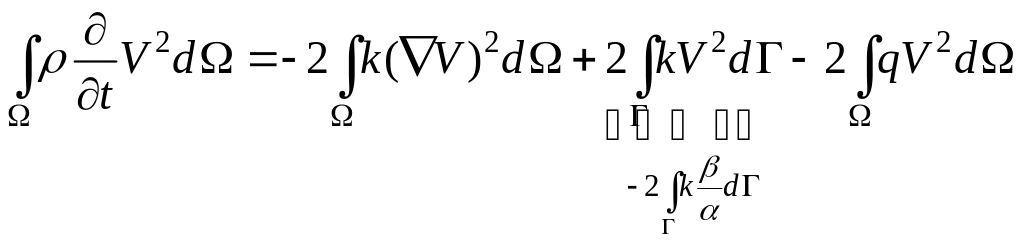
В случае I краевой задачи:

II краевой задачи:

Ш краевой задачи:

Проинтегрируем полученное равенство в пределах от 0 до

(Для III краевой задачи применяется это равенство, а для I и II – справа без третьего интеграла).

Конец доказательства.

Крутильные колебания вала с диском на конце.

Уравнением крутильных колебаний вала, как уже было показано в первом семестре, является уравнение: .

Предположим теперь, что один конец вала закреплен, а к другому концу прикреплен диск, момент инерции которого относительно оси вала равен . В начальный момент времени диск закручивается на угол и опускается без начальной скорости.

Длина дуги с одной стороны - , а с другой стороны - , - длина вала, - угол поворота.

- модуль сдвига

- момент инерции вала

Если бы на правом конце вала диск отсутствовал, то в силу отсутствия внешних сил вращающий момент

Так как в нашем случае роль внешней силы играет диск, то произведение момента инерции этого диска на его угловое ускорение и даст значение крутящего момента, то есть , - угловое ускорение.

Отсюда граничное условие принимает вид: , если обозначить граничное условие запишется .

Тогда математическая модель задачи:

Решение этой задачи будем искать в виде , подставляем в уравнение:

, , .

Из что

разделим на

;

Тогда . Пусть .

Обозначим через – корни уравнения, тогда – собственные значения, – собственные функции.

.

Подтвердим ортогональность функций , . Для этого найдём:

не является ортогональным на отрезке .

Проверим ортогональность

производные ортогональны.