Классификация уравнений второго порядка в точке (в области).

Рассмотрим дифференциальное уравнение (1). Коэффициент является непрерывной функцией. Выясним закон преобразования коэффициентов уравнения (1) при замене причем предполагается Якобиан преобразования. Если то Выразим производные по старым переменным через новые

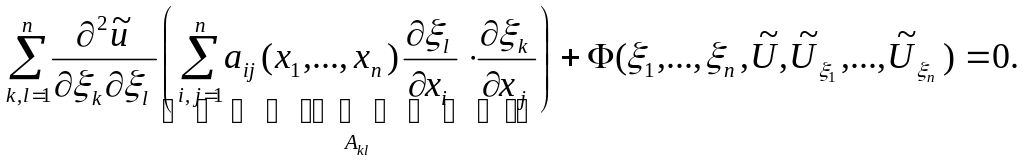
Обозначим через (2). В (2) введем обозначения Тогда (2^*). Выражение (2^*) совпадает в фиксированной точке с формулой преобразования коэффициентов квадратичной формы при линейном преобразовании переводящее исходную квадратичную в квадратичную форму

Таким образом, чтобы упростить в фиксированной точке уравнение (1) достаточно упростить в этой точке соответствующую уравнению квадратичную форму. Эта квадратичная форма в точке имеет вид:

Из алгебры известно, что любая квадратичная форма с помощью неособого линейного преобразования может быть приведена к виду: При этом коэффициент может принимать значения -1, 0, 1.

Будем говорить, что уравнение относится к гиперболическому типу, если в каноническом виде квадратичной формы все за исключением 1 – го имею один знак, а этот один противоположного знака.

Уравнение (1) в точке относится к эллиптическому, если все и имеют один знак.

Параболического типа, если один из коэффициентов а все остальные одного знака ( ).

Несколько иначе обстоит дело в случае двух независимых переменных. Уравнение имеет вид: (3).

Составим квадратичную форму с переменными коэффициентами:

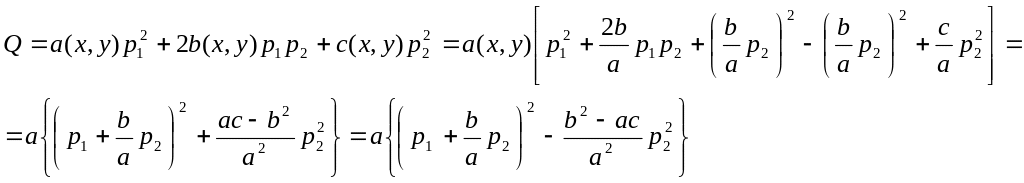
Характеристическая поверхность (Характеристики).

(1)

Пусть некоторая функция один раз непрерывно – дифференцируемая, такая, что на поверхности не все частные производные равны 0.

(2), тогда поверхность называется характеристической поверхностью уравнения (1) или характеристикой этого уравнения, а уравнение (2) называется характеристическим уравнением или уравнением характеристики.

Предположим, что каждая поверхность семейства является характеристикой уравнения (1). Так как на каждой характеристике то это семейство заполняет некоторую достаточно малую область пространства и через каждую точку этой области проходит одна характеристика. Если потребовать

то взяв в качестве новой переменной получим, что коэффициенты преобразованного уравнения имеют вид:

таким образом, знание одной характеристики уравнения (1) позволяет с помощью замены сделать один из коэффициентов преобразованного уравнения нулевым.

Приведение к каноническому виду уравнения 2 – го порядка в случае

2 – х независимых переменных.

Рассмотрим уравнение . (1)

Выясним закон преобразования этого уравнения путем замены (2) при

После применения (2) мы перейдем к уравнению

(3)

Выразим производные по через производные по

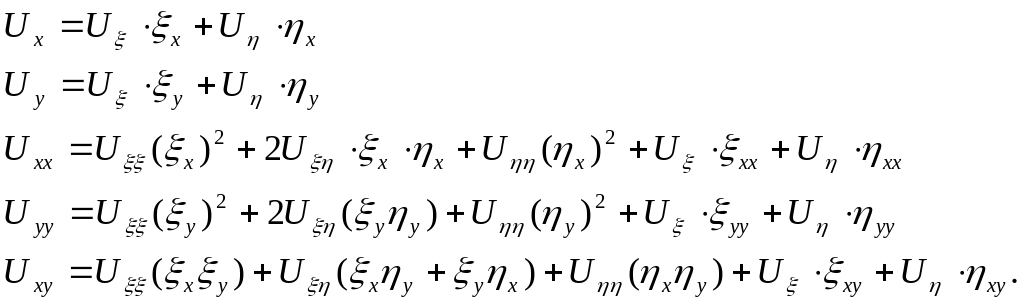
Подставим найденные значения производных в уравнение (1) и выпишем коэффициенты при вторых производных по

(4)

Предположим, что уравнение (1) мы рассматриваем в области, где Уравнением характеристик для уравнения (1) будет уравнение

Положим в (4) - уравнение характеристик. Коэффициент в рассматриваемой области отличен от нуля, если же , то считаем, что

(5)

Пусть - общие интегралы последних двух уравнений.

В уравнении (1) сделаем замену

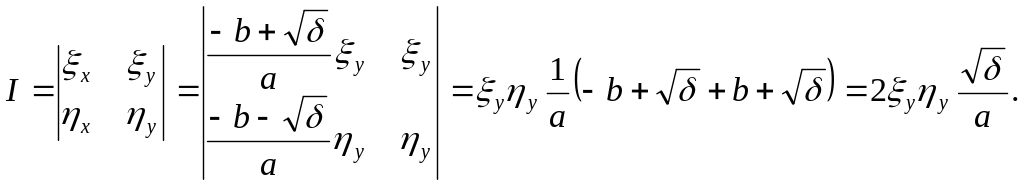
При выбранной замене переменных коэффициент обращается в нуль. Так как коэффициент отличатся от только от искомой функции, то коэффициент тоже обращается в нуль.

Коэффициент в силу инвариантности типа уравнения отличен от нуля и разделив на удвоенные коэффициенты уравнение (3) мы получим канонический вид уравнения гиперболического типа.

Рассмотрим случай, когда - уравнение параболического типа. Тогда уравнение характеристик распадается на 2 совпадающих уравнения и мы можем найти только один интеграл, соответствующая система в симметричной форме, который определяется формулой:

Пусть - интеграл последнего уравнения. Сделаем замену положим где - произвольная дважды непрерывно – дифференцируемая функция и такая, что

Рассмотрим коэффициент

Разделив уравнение (3) на придем к каноническому виду уравнения параболического типа

Рассмотрим теперь случай

Тогда уравнение характеристик примет вид:

Пусть - комплекснозначные интегралы характеристического уравнения , сделаем замену

Подставим в уравнение характеристик:

Разделив уравнение (3) на коэффициенты получим канонический вид уравнения эллиптического типа

Приведение к каноническому виду уравнений второго порядка с постоянными коэффициентами в случае независимых переменных.

Рассмотрим уравнение второго порядка (1), в котором коэффициенты - постоянны. Соответствующая этому уравнению квадратичная форма имеет вид: Эта квадратичная форма с помощью замены переменных при соответствующем выборе не особой матрицы приводится к каноническому виду ,

Уравнение (1) с помощью замены может быть приведено к виду

Установим связь между матрицами и . Для простоты рассуждения рассмотрим уравнение с двумя переменными.

(2), в котором коэффициенты постоянные, соответствующая этому уравнению квадратичная форма

Сделаем замену

В уравнении (1) сделаем замену: тогда

То есть,

Классические задачи УМФ и задачи, корректно поставленные для них.

Гиперболический тип – описывает колебательные явления.

Уравнение колебаний струны имеет вид: - одномерное волновое уравнение (ОВУ) или (ВУ1), где некоторая постоянная, - задана на некотором множестве непрерывная функция.

То есть мы получили смешанную задачу.

Задача Коши -

Параболический тип – описываются процессы теплопроводности и диффузии.

Уравнение теплопроводности (одномерное)

Эта будет смешанная задача.

Эллиптический тип – описывает стационарные процессы ( т.е. явления, которые не меняются с течением времени ).

- уравнения Лапласа.

- уравнение Пуассона.

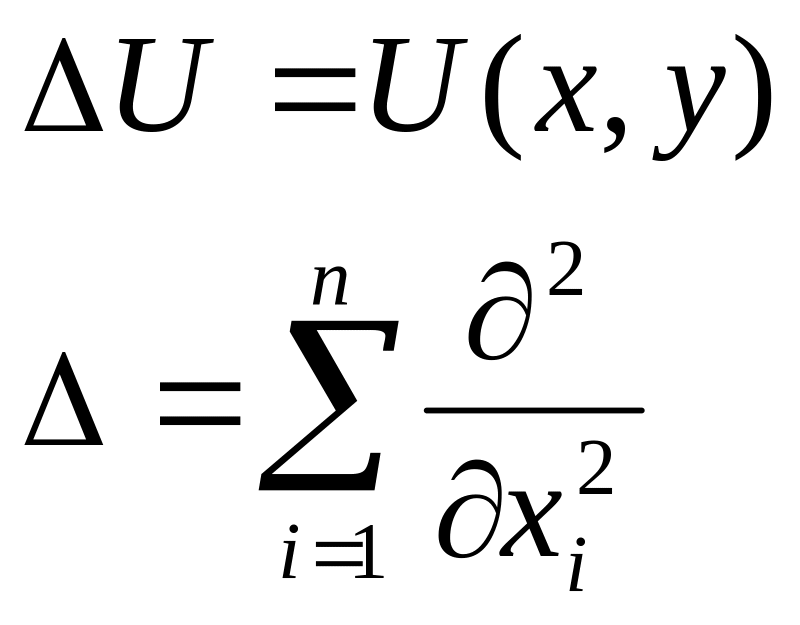либо

Например:

1) - уравнение Дирихле (первая краевая задача).

2) - задача Неймана (вторая краевая задача).

3) - 3-я краевая задача.

Теорема Ковалевской.

Система дифференциальных уравнений с неизвестными функциями с 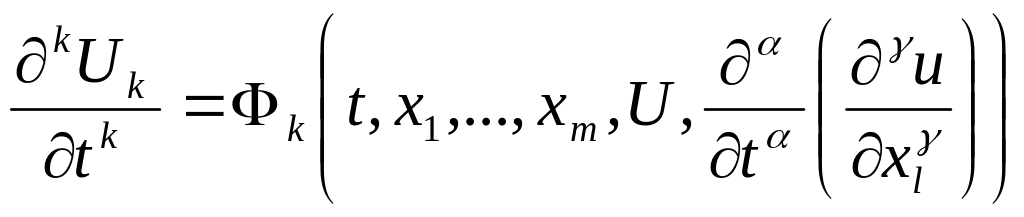называется нормальной относительно переменной если в правой части не содержит производных по порядка выше и производные по порядка выше

- нормальная система.

Функция будет аналитической в точке если она в окрестности этой точки представлена в виде: где

Пусть дана в точке то она представляется в виде:

Для нормальной системы в частных производных поставим задачу Коши: Найти решение этой системы, удовлетворяющее начальным условиям: 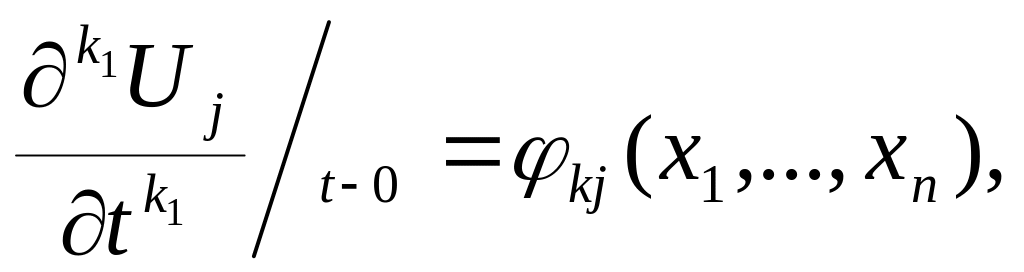где ,

Теорема: (Ковалевской) Если все функции аналитичны в

некоторой окрестности точки и все

функции являются аналитическими

функциями своих аргументов в некоторой

окрестности точки то

задача Коши имеет аналитическое решение в

некоторой окрестности точки

причем единственное в классе аналитических

функций.

Теорема Ковалевской, не смотря на ее общий характер, гарантирует единственное решение только в некоторой достаточно малой окрестности точки Обычно, если система уравнений в частных производных описывается реальным физическим процессом, то требуется установить существование и единственность решения в некоторой достаточно большой области, поэтому делаем вывод, что теорема Ковалевской не полностью решает вопрос о корректности постановки задачи Коши для нормальной системы в частных производных.

Понятие и корректность постановки задач УМФ. Пример Адамара.

При моделировании реально протекающих физических или иных явлений получают либо обыкновенные дифференциальные уравнения (системы) либо уравнения в частных производных. Понятно, что в этом случае нас будут интересовать не решения уравнения вообще, а решение этого уравнения, описывающие реальные физические явления. Для этого кроме уравнения на решение накладываются дополнительные условия (начальные и граничные).

Задача считается корректно поставленной, если:

1. решение этой задачи существует;

2. решение должно быть единственным;

3. как правило, начальные и граничные условия в реальных физических задачах получается путем измерения , а следовательно, не могут быть точным, а значит при различных измерениях будут отличаться друг от друга. Последнее означает, что при правильной постановке задачи малое измерение начальных и граничных условий должно приводить к малому изменению решения, то есть решение должно быть устойчиво (при корректно поставленной задаче).

Приведем пример задачи, не корректно поставленной.

- не корректно поставленная задача.

Легко привести примеры задач, в которых нарушается единственность решения.

Пример:

поставлена некорректно, так как решением является функция

Приведем пример задачи, в которой нарушается устойчивость решений (пример Адамара).

Рассмотрим задачу :

и - некоторые известные функции.

Пусть - решение задачи. Рассмотрим еще одну задачу:

Пусть - решение этого уравнения. Составим разность тогда - решение задачи

при

Найдем решение задачи для функции в виде

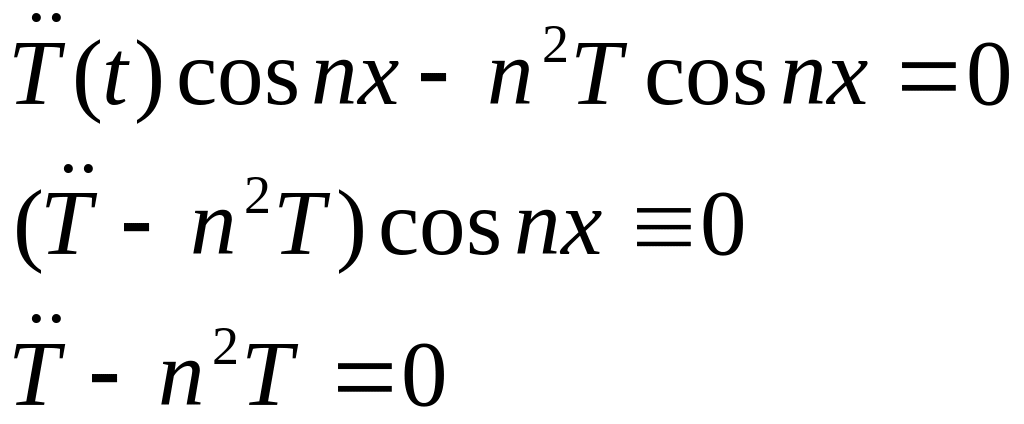
, - задача Коши для лин. уравнения с пост.коэф.2 – го пор.

.

Таким образом,

Малые изменения начальных данных привели к большой разности решений.

Покажем, что задача Коши для уравнения Лапласа поставлена некорректно.

Задачи, приводящие к уравнениям различных типов. Уравнение колебаний струны.

Под струной мы будем понимать упругую нить, не оказывающую сопротивление изгибу, но оказывающую сопротивление растяжению.

Отсутствие сопротивления изгибу математически выражается тем, что напряжение, возникающее в струне, всегда направлено по касательной к ее мгновенному профилю.

Будем рассматривать струну, расположенную вдоль оси и совпадающую с этой осью в состоянии покоя.

В процессе колебаний струну (точки струны) будут отклоняться от этой оси. Величина этого отклонения ( ) зависит от времени и от координат точки струны ( ). Будем рассматривать только малые поперечные колебания струны. Малость колебаний означает, что величинами можно пренебречь.

Рассмотрим теперь участок струны между и В процессе колебания этот участок деформируется в дугу Длина недеформированного участка 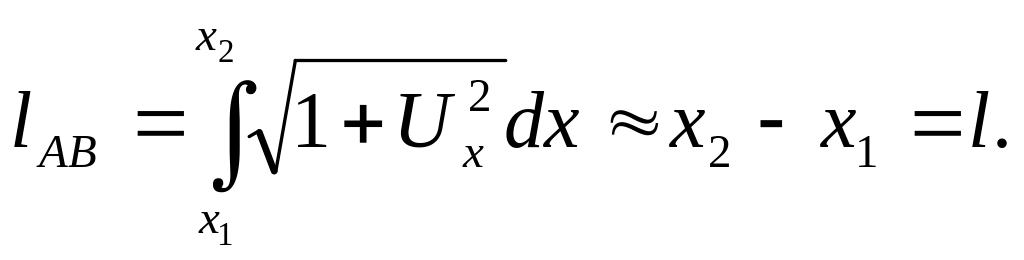Если

Таким образом, в процессе малых колебаний струны изменение струны не происходит. На основании закона Гука приходим к выводу, что в процессе колебаний сила натяжения струны не меняется.

Так как мы рассматриваем только поперечные колебания струны, то есть все точки струны могут двигаться только в направлении 1, то нас будут интересовать проекции всех сил, приложен к точкам струны на ось

Рассмотрим участок струны длиной

Обозначим через величину силы,

приложенной в момент времени к

точке Пусть линейная плос-

кость струны (масса участка струны),

тогда масса участка длиной будет

равна .

(проекция ускорения на ось ).

уравнение колебаний струны.

где

уравнение свободных колебаний струны.