Внешнее соединение

Операция соединения приведет к отношению, в котором перечислены студенты и предметы, на которые они записаны. Студенты, не записанные ни на один из предметов, не будут представлены в результатах. Если мы хотим включить в ре­зультирующее отношение всех студентов, можно использовать внешнее соедине­ние (outer join). Так, в результате операции левого внешнего соединения (left outer join), имеющей вид СТУДЕНТ LEFT OUTER JOIN (ЛичныйНомер= НомерСтудента) ЗАПИСЬ, получится отношение, в котором будут присутствовать все строки из отношения СТУДЕНТ. Данное отношение представлено на рис. 8.16, в. В нем фигурирует студент Смит, хотя этот студент не записан ни на один из предметов. Ключевое слово LEFT (левый) указывает, что в результате должны быть представлены все строки из отношения, находящегося по левую сторону от оператора соединения (в нашем случае это отношение СТУДЕНТ). Операция правого внешнего соединения (right outer join), имеющая вид СТУДЕНТ RIGHT OUTER JOIN (ЛичныйНомер = НомерСтудента) ЗАПИСЬ, приведет к отношению, в котором будут присутствовать все строки из таблицы, находящейся справа от оператора соединения, — а именно таблицы ЗАПИСЬ. Внешнее соединение удобно использовать при работе со связями, в ко­торых минимальное кардинальное число равняется нулю с одной или с обеих сторон. Иногда, когда во избежание неоднозначности требуется указать, какой именно тип соединения имеется в виду, вместо термина соединение используется термин внутреннее соединение (inner join).

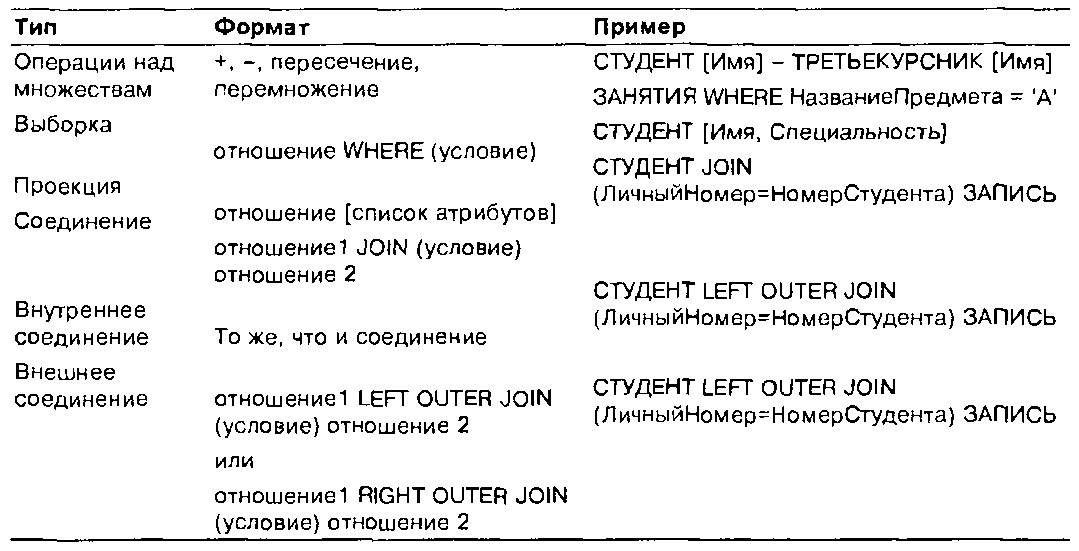
Выражение запросов в терминах реляционной алгебры

В табл. 8.2 перечислены все основные операции реляционной алгебры, описан­ные выше. Из них стандартными операциями теории множеств являются объ­единение (+), вычитание (-), пересечение и произведение. Операция выборки выделяет из отношения определенные кортежи (строки) в соответствии с усло-пнями, наложенными на значения атрибутов. Операция проектирования выделя­ет из отношения атрибуты (столбцы) по заданным именам. Наконец, операция соединения конкатенирует кортежи двух отношений в соответствии с условием, наложенным на значения атрибутов.

Теперь посмотрим, как с помощью реляционных операторов можно фор­мулировать запросы. Воспользуемся для этого отношениями СТУДЕНТ, ЗАНЯТИЯ и ЗАПИСЬ, показанными на рис. 8.12. Данные для примера представлены на рис. 8.17. Наша цель состоит в том, чтобы продемонстрировать различные операции с отношениями. Хотя вы, скорее всего, не будете использовать реляционную алгебру при работе с коммерческими продуктами, эти примеры помогут вам понять, каким образом можно манипулировать отношениями.

1. Вывести имена всех студентов. Студент [Имя]

Эта строка проектирует отношение СТУДЕНТ на атрибут Имя. Результатом является следующая таблица:

джонс

ПАРКС БЕЙКЕР

Гласс рассел рай

Повторяющиеся имена могут быть опущены. Хотя имена Джонс и Бейкер фигурируют в отношении СТУДЕНТ дважды, повторения были исключены, поскольку результат проектирования представляет собой отношение, а от­ношение не может содержать одинаковые кортежи.

. Вывести имена студентов, записанных хотя бы на один предмет.

ЗАПИСЬ [НомерСтудента]

Этот запрос похож на первый, но здесь оператор проектирования действу­ет на отношение ЗАПИСЬ. Результатом является следующая таблица:

100 150 200 300 400 450

Как и в предыдущем примере, одинаковые строки были удалены. Вывести номера студентов, не записанных ни на один предмет. СТУДЕНТ [ЛичныйНомер] - ЗАПИСЬ [НомерСтудента]

Это выражение представляет собой разность между проекциями двух от­ношений: проекция СТУДЕНТ [ЛичныйНомер] содержит номера всех студен­тов, а проекция ЗАПИСЬ [НомерСтудента] содержит номера студентов, запи­санных на какие-либо предметы. Их разность — это номера студентов, не записанных ни на один предмет. Результатом является следующая таблица:

250 350

298