
- •Введение
- •2 Физические величины и измерения
- •2.1 Исходные понятия и определения
- •2.2 Единицы физических величин
- •2.3. Классификация измерений
- •3 Средства измерений
- •3.1 Классификация средств измерений
- •3.2 Структура средств измерений
- •3.3 Характеристики средств измерений
- •Метрологические характеристики. Функция преобразования – функциональная зависимость между информативн6ым параметром выходного и входного сигналов средства измерения:
- •Неметрологические характеристики
- •Нормирование метрологических характеристик.
- •4 Погрешности измерений
- •4.1 Понятие о шкалах измерений
- •4.2 Основной постулат метрологии
- •Тогда абсолютная погрешность измерения
- •5 Фактор погрешностей
- •Отсюда погрешность измерения, называемая абсолютной
- •5.1 Систематические и случайные погрешности
- •5.1.1 Систематические погрешности
- •5.1.2 Случайные погрешности
- •5.2 Оценивание погрешностей результатов измерений
- •5.2.1 Прямое многократное измерение
- •Тогда оценкой дисперсии при ограниченном числе наблюдений будет:
- •5.2.2 Прямое однократное измерение
- •5.2.3 Косвенные измерения
Неметрологические характеристики
При эксплуатации измерительных приборов и других средств измерений важно знать и неметрологические характеристики: показатели надежности, электрической прочности, сопротивления и изоляции и др.
Одной из основных характеристик является метрологическая надежность средства измерения, под которой понимают свойство средств измерений сохранять установленные значения метрологических характеристик в течение определенного времени при нормальных режимах и рабочих условиях эксплуатации. Выход одной или более метрологических характеристик средства измерения за пределы нормы приводит к метрологическому отказу. Для оценки метрологической надежности используют показатели: наработка на отказ, срок службы и ресурс, среднее время восстановления средства.
Нормирование метрологических характеристик.
Главная из нормируемых характеристик – погрешность. Пределы допускаемых основной и дополнительной погрешности выражают в форме приведенных, относительных или абсолютных погрешностей.
Предел допускаемой абсолютной основной погрешности, выраженной в единицах измеряемой величины или условно в делениях шкалы, устанавливают по формуле
![]()
![]() (3.1)
(3.1)
![]() (3.2)
(3.2)
где
![]() –
значение измеряемой величины, а
и b
положительные числа не зависящие от
(а
– предельное значение аддитивной
погрешности, b
–коэффициент при предельном значении
мультипликативной погрешности).
–
значение измеряемой величины, а
и b
положительные числа не зависящие от
(а
– предельное значение аддитивной
погрешности, b
–коэффициент при предельном значении
мультипликативной погрешности).
Предел допускаемой приведенной основной погрешности устанавливают по формуле (в процентах)
![]() (3.3)
(3.3)
где
![]() - предел допускаемой абсолютной основной
погрешности, xN
- нормирующие
значение – условно принятое значение
измеряемой величины,
- предел допускаемой абсолютной основной
погрешности, xN
- нормирующие
значение – условно принятое значение
измеряемой величины,
![]() –
отвлеченное положительное число.
–
отвлеченное положительное число.
Предел допускаемой относительной погрешности устанавливают по формуле ( в процентах)
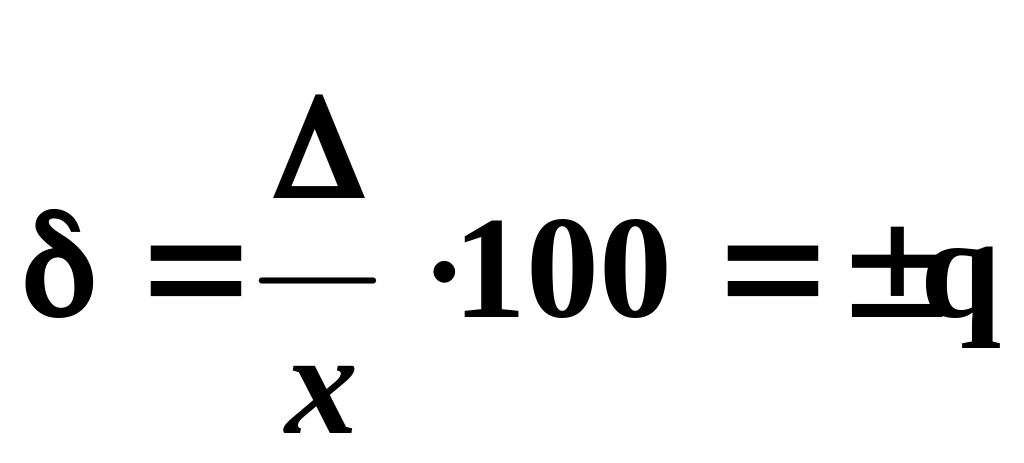 , (3.4)
, (3.4)
если устанавливают по формуле 3.1, или
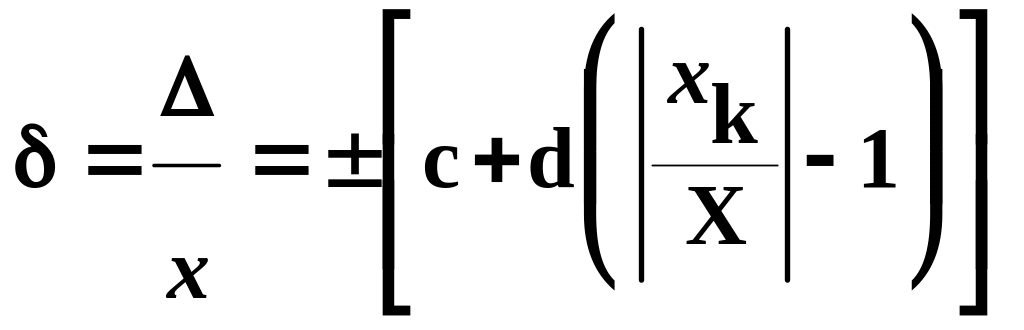 , (3.5)
, (3.5)
если устанавливают по формуле 3.2. в этих выражениях q– отвлеченное положительное число, xk– больший по модулю из пределов измерений, с и d– положительные числа, причем
![]()
Всем средствам измерений присваивается определенный класс точности. Класс точности – обобщенная метрологическая характеристика, определяемая пределами допускаемых погрешностей. Класс точности может выражаться одним числом или двумя числами, разделенными чертой и реже римскими цифрами или латинскими буквами.
Для
обозначения классов точности используется
значение чисел
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
выбранные из ряда 1 · 10 n;
1,5 · 10 n;
2 · 10 n
; 2,5 · 10 n;
4 · 10 n;5
·10n;
6 · 10 n;
где n
= 1, 0, -1, -2, …..
,
выбранные из ряда 1 · 10 n;
1,5 · 10 n;
2 · 10 n
; 2,5 · 10 n;
4 · 10 n;5
·10n;
6 · 10 n;
где n
= 1, 0, -1, -2, …..
Например:
класс точности 2,5 означает, что предел
допускаемой основной погрешности
установлен по формуле 3.3
![]() ;
класс точности
;
класс точности
![]() –
по формуле 3.4
–
по формуле 3.4
![]() ;
класс точности 0,02/ 0,01 – по формуле 3.5 (с
= 0,02; d
= 0,01); класс точности М
– по формуле 3.1; класс точности с
– по формуле 3.2.
;
класс точности 0,02/ 0,01 – по формуле 3.5 (с
= 0,02; d
= 0,01); класс точности М
– по формуле 3.1; класс точности с
– по формуле 3.2.
4 Погрешности измерений
4.1 Понятие о шкалах измерений
Любое измерение предполагает получение информации о размере физической величины путем сравнения неизвестного размера измеряемой величины с известным и выражением первого через второй.
Простейший способ получения такой информации, состоит в сравнении по принципу «Что больше (меньше)». Расположение по этому принципу размеры измеряемых величин образуют шкалу порядка. Особенно широкое распространение такие шкалы получили в областях, где измерения с помощью технических средств не достигли высокого совершенства (в гуманитарных науках, искусстве и т.д.). недостатками таких шкал является неопределенность интервалов между опорными точками (например шкала вида: неудовлетворительно, удовлетворительно, хорошо, отлично). Результаты измерений по этим шкалам нельзя складывать, вычитать, перемножать, делить.
Более совершенными в этом отношении являются шкалы, составленные из строго определенных интервалов – шкалы интервалов. По шкале интервалов можно судить не только о том, что один размер больше другого, но и о том, на сколько больше, т.е. на шкале интервалов можно выполнять такие математические действия как сложение и вычитание (временные шкалы, шкала температур Цельсия и т.п.).
Но, если на шкале интервалов выбрать точку, в которой размер физической величины равен нулю (не принимается равным нулю, а действительно равен нулю), то по этой шкале уже можно отсчитывать абсолютное значение размера и определять не только, на сколько этот размер больше или меньше другого, но и во сколько раз он больше или меньше. Эта шкала называется шкалой отношений.
Шкала отношений является наиболее совершенной из всех рассмотренных шкал. На ней можно выполнять операции сложения, вычитания, деления и умножения. Большинство физических величин электрической природы измеряется с использованием этой шкалы.
