4.4. Еквівалентність схем
Розробники схем часто намагаються скоротити число вентилів, щоб знизити ціну, зменшити площу схеми, скоротити споживання енергії і т.д. Щоб спростити схему, розробник повинний знайти іншу схему, що може обчислювати ту ж функцію, але при цьому вимагає меншої кількості вентилів (або може працювати з більш простими вентилями, наприклад двовходовими замість чотиривходових). Булева алгебра є інструментом у пошуку еквівалентних схем.
Як приклад використання булевої алгебри розглянемо схему і таблицю істинності для АВ+АС (рис. 4.5 а). Багато правил звичайної алгебри мають силу для булевої алгебри. Наприклад, вираз АВ+АС може бути перетворений в А(В+С) за допомогою дистрибутивного закону. На рис. 4.5 б показана схема і таблиця істинності для А(В+С). Дві функції є еквівалентними тоді і тільки тоді, коли обидві функції приймають те саме значення для всіх можливих змінних. З таблиць істинності на рис. 4.5 видно, що А(В+С) еквівалентно АВ+АС. Незважаючи на цю еквівалентність, схема на рис. 4.5 б краща, ніж схема на рис. 4.5 а, оскільки вона містить менше вентилів.
Як правило, розробник виходить з визначеної булевої функції, а потім застосовує до неї закони булевої алгебри, щоб знайти більш просту функцію, еквівалентну вихідній. На основі отриманої функції можна конструювати схему.
Щоб
використовувати даний підхід, потрібні
деякі рівності з булевої
алгебри.
У табл. 1 показані деякі основні закони.
Треба відзначити, що кожний
закон має дві
форми.
Одну форму з іншої можна одержати,
змінюючи І на АБО
і 0 на 1.
Усі
закони можна легко довести, склавши
їхні
таблиці істинності.
Майже у всіх випадках результати
очевидні, за винятком законів де
Моргана,
законів поглинання і дистрибутивного
закону А+ВС=(А+В)(А+С). Закони де
Моргана
поширюються
на вирази
з
більше ніж двома змінними, наприклад
.
A |
В |
С |
АВ |
АС |
АВ+АС |
|
А |
В |
С |
А |
В+С |
А(В+С) |
А |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
|
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
а) б)
Рис. 4.5. Дві еквівалентні функції: АВ+АС (а); А(В+С) (б).
Таблиця 5.1 - Деякі закони булевої алгебри
Назви законів |
І |
АБО |
Закони тотожності |
1А=А |
0+А=А |
Закони нуля |
ОА=0 |
1+А=1 |
Закони ідемпотентності |
АА=А |
А+А=А |
Закони інверсії |
А |
А+ =1 |
Комунікативні закони |
АВ=ВА |
А+В=В+А |
Асоціативні закони |
(АВ)С=А(ВС) |
(А+В)+С= А+(В+З) |
Дистрибутивні закони |
А+ВС= (А+В)(А+С) |
А(В+С)=АВ+АС |
Закони поглинання |
А(А+В)=А |
А+АВ=А |
1 |
2 |
3 |
Закони Де Моргана |
|
|
=0
Закони Де Моргана припускають альтернативний запис. На рис. 4.6 а форма І дається із запереченням, що показується за допомогою інвертуючи входів і виходів. Таким чином, вентиль АБО з інвертованими вхідними сигналами еквівалентний вентилеві НЕ-І. З рис. 4.6 б, на якому зображена друга форма закону Де Моргана, ясно, що замість вентиля НЕ-АБО можна намалювати вентиль І з інвертованими входами. За допомогою заперечення обох форм закону Де Моргана приходимо до еквівалентних репрезентацій вентилів І і АБО (див. рис. 4.6 в і 4.6, г). Аналогічні символічні зображення існують для різних форм закону Де Моргана (наприклад, n-вхідний вентиль НЕ-І стає вентилем АБО з інвертованими входами).
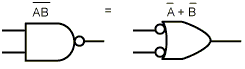
а) б)
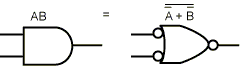
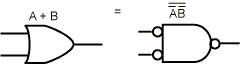
в) г)
Рис. 4.6 - Альтернативні позначення деяких вентилів: НЕ-І (а); НЕ-АБО (б); І (в); АБО (г)
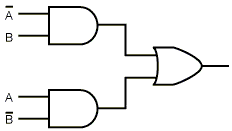
Використовуючи рівняння, зазначені на рис. 4.6 і аналогічні рівняння для багатовхідних вентилів, можна легко перетворити суму добутків у чисту форму НЕ-І або чисту форму НЕ-АБО.
Як
приклад розглянемо
функцію
ВИКЛЮЧНЕ
АБО
(рис. 4.7 а).
Стандартна
схема,
що
виражає
суму добутків,
показана на рис. 4.7 б.
Щоб
перейти до форми НЕ-І, потрібно
лінії,
що
з'єднують виходи вентилів І з входом
вентиля АБО,
намалювати з
інвертуючими входами і
виходами,
як показано на
рис. 4.7
в.
Потім,
застосовуючи
рис. 4.6 а,
приходимо до рис. 4.7 г.
Змінні
і
можна одержати
з
А і В, використовуючи вентилі НЕ-І або
НЕ-АБО з
об'єднаними входами. Відзначимо,
що інвертуючі входи
(виходи)
можуть переміщатися уздовж лінії за
бажанням,
наприклад,
від виходів вхідних вентилів до входів
вихідного
вентиля.
А |
У |
XOR |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
а) б)
в) г)
Рис. 4.7 - Таблиця істинності для функції ВИКЛЮЧнЕ АБО (а); три схеми для обчислення цієї функції (б-г)
Дуже важливо відзначити, що той самий вентиль може обчислювати різні функції в залежності від використовуваних угод. На рис. 8 а показано вихід певного вентиля, F, для різних комбінацій вхідних сигналів. І вхідні, і вихідні сигнали показані у вольтах. Якщо прийняти угоду, що 0 В – це логічний нуль, а 3,3 В або 5 В – логічна одиниця, одержимо таблицю істинності, показану на рис. 4.8 б, тобто функцію І. Така угода називається позитивною логікою. Однак якщо прийняти негативну логіку, тобто прийняти, що 0 В – це логічна одиниця, а 3,3 В або 5 В – логічний нуль, то одержимо таблицю істинності, показану на рис. 4.8 в, тобто функцію АБО.
Таким чином, все залежить від того, яка угода обрана для відображення вольтів у логічних величинах.
A
В
F
1
1
1
1
0
1
0
1
1
0
0
0
А
В
F
0v
0v
0v
0v
5v
0v
5v
0v
0v
5v
5v
5v
A
В
F
0
0
0
0
1
0
1
0
0
1
1
1
а) б) в)
Рис.5.8 - Електричні характеристики пристрою (а); позитивна логіка (б); негативна логіка (в)