4.3. Реалізація булевих функцій
Отже, представлення булевої функції у вигляді суми максимум 2п добутків уможливлює реалізацію цієї функції. На рис. 4.3 можна побачити, як це здійснюється. На рис. 4.3 б вхідні сигнали А, В і С показані з лівої сторони, а функція М, отримана на виході, показана з правої сторони. Оскільки необхідні додаткові величини (інверсії) вхідних змінних, вони утворюються шляхом проходження сигналу через інвертори 1,2 і 3. З 6 вертикальних ліній 3 пов'язані з вхідними змінними, а 3 інші – з їх інверсіями. Ці лінії забезпечують передачу вхідного сигналу до вентилів. Наприклад, вентилі 5, 6 і 7 як вхід використовують А. У реальній схемі ці вентилі, імовірно, будуть безпосередньо з'єднані проводом з А без яких-небудь проміжних вертикальних проводів.
Схема містить чотири вентилі І, по одному для кожного члена в рівнянні для М (тобто по одному для кожного рядка в таблиці істинності з результатом 1). Кожен вентиль І обчислює один із зазначених рядків таблиці істинності. Зрештою всі дані добутки сумуються (мається на увазі операція АБО) для одержання кінцевого результату.
Якщо дві лінії на малюнку перетинаються, зв'язок є в тому випадку, якщо на перетинанні зазначена жирна крапка. Наприклад, вихід вентиля 3 перетинає всі 6 вертикальних ліній, але пов'язаний він тільки із С.
Реалізувати схему для будь-який булевої функції можна за такі етапи:
Скласти таблицю істинності для даної функції.
Забезпечити інвертори, щоб потворити інвер-сії для кожного вхідного сигналу.
Намалювати вентиль І для кожного рядка табли-ці істинності з результатом 1.
З'єднати вентилі І з відповідними вхідними сигналами.
Вивести виходи усіх вентилів І у в вентиль АБО.
У даному прикладі показано, як реалізувати будь-яку булеву функцію з використанням вентилів НЕ, І і АБО. Однак набагато зручніше будувати схеми з використанням одного типу вентилів. Схеми, побудовані по попередньому алгоритмі, можна легко перетворити у форму НЕ-І або НЕ-АБО. Щоб здійснити таке перетворення, усе, що потрібно – це спосіб реалізації НЕ, І і АБО за допомогою одного типу вентилів. На рис. 4.4 показано, як це можна зробити, використовуючи тільки вентилі НЕ-І або тільки вентилі НЕ-АБО. Відзначимо, що існують також інші способи подібного перетворення.
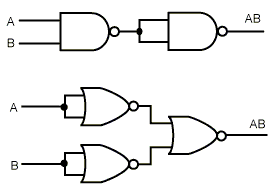
а) б)
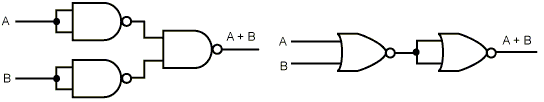
в)
Рис. 4.4 - Конструювання вентилів НЕ (а), І (б) і АБО (в) з використанням тільки вентилів НЕ-І або тільки вентилів НЕ-АБО
Для того щоб реалізувати булеву функцію з використанням тільки вентилів НЕ-І або тільки вентилів НЕ-АБО, можна спочатку додержуватися алгоритму, описаному вище, і сконструювати схему з вентилями НЕ і І і АБО. Потім потрібно замінити багатовхідні вентилі еквівалентними схемами з використанням двоходових вентилів. Наприклад, A+B+C+D можна поміняти на (A+B)+(C+D), використовуючи три двовходові вентилі. Потім вентилі НЕ і І і АБО заміняються схемами, зображеними на рис. 4.4.
Хоча така процедура і не приводить до оптимальних схем з погляду мінімального числа вентилів, вона демонструє, що подібне перетворення здійсненне. Вентилі НЕ-І і НЕ-АБО вважаються повними, тому що можна обчислити будь-яку булеву функцію, використовуючи тільки вентилі НЕ-І або тільки вентилі НЕ-АБО. Інші вентилі не мають такої властивості, от чому саме ці два типи вентилів кращі при побудові схем.