4.2. Булева алгебра

Щоб описати схеми, що будуються шляхом сполучення різних вентилів, потрібний особливий тип алгебри, у якій усі змінні і функції можуть приймати тільки два значення: 0 і 1. Така алгебра називається булевою алгеброю. Вона названа на честь англійського математика Джорджа Буля (1815-1864). Насправді в даному випадку мається на увазі особливий тип булевої алгебри, а саме алгебра релейних схем.

Булева функція має одну або декілька змінних і видає результат, що залежить тільки від значень цих змінних. Можна визначити просту функцію f, сказавши, що f(A)=l, якщо А=0, і f(A)=0, якщо А=1. Така функція буде функцією НЕ (рис. 4.2 а).

Внаслідок того, що булева функція від n змінних має тільки 2^п можливих комбінацій значень змінних, то таку функцію можна цілком описати в таблиці з 2^п рядками. У кожному рядку буде даватися значення функції для різних комбінацій значень змінних. Така таблиця називається таблицею істинності. Усі таблиці на рис. 4.2 являють собою таблиці істинності. Функцію можна цілком описати 2^п-бітним двійковим числом, що виходить, якщо зчитувати по вертикалі колонкові результати у таблиці істинності. Таким чином, НЕ-І – це 1110, НЕ-АБО - 1000, І - 0001 і АБО - 0111. Очевидно, що існує тільки 16 булевих функцій від двох змінних, яким відповідають 16 можливих 4-бітних ланцюжків. У звичайній алгебрі, навпаки, є нескінченне число функцій від двох змінних, і ні одну з них не можна описати, давши таблицю значень цієї функції для всіх можливих значень змінних, оскільки кожна змінна може приймати нескінченне число значень.

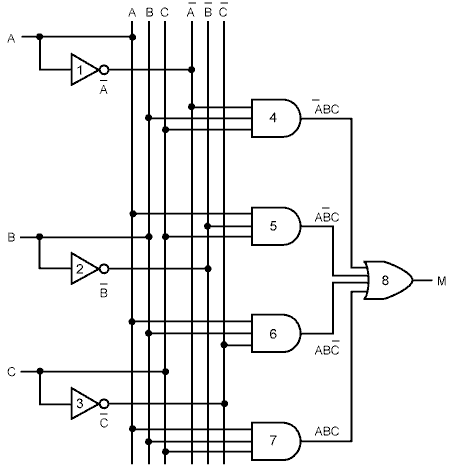
На рис. 4.3 а показана таблиця істинності для булевої функції від трьох змінних: M=f(A, В, С). Це функція більшості, яка приймає значення 0, якщо більшість змінних дорівнює 0, і 1, якщо більшість змінних дорівнює 1. Хоча будь-яка булева функція може бути визначена за допомогою таблиці істинності, зі зростанням кількості змінних такий тип запису стає громіздким. Тому замість таблиць істинності часто використовується інший тип запису.

Щоб побачити, яким чином здійснюється цей інший тип запису, відзначимо, що будь-яку булеву функцію можна визначити, вказавши, які комбінації значень змінних дають

А	В	С	М
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

a)

б)

Рис. 4.3 - Таблиця істинності для функції більшості від трьох змінних (а); схема для цієї функції (б).

значення функції 1. Для функції, приведеної на рис. 4.3 а, існує 4 комбінації змінних, які дають значення функції 1.

Знак множення будемо використовувати позначення булевої функції І (знак множення може опускатися) і “+” для позначення булевої функції АБО. Наприклад, A C приймає значення 1, тільки якщо А=1, В=0 і С=1. А +В приймає значення 1, тільки якщо (А=1 і В=0) або (В=1 і С=0). У таблиці на рис. 4.3, а функція приймає значення 1 у чотирьох рядках: ВС, A C, AB і ABC. Функція М приймає значення істини (тобто 1), якщо одне з цих чотирьох умов істинно. Отже, можна написати

М= ВС+ A C+ AB + ABC.

Це компактний запис таблиці істинності. Таким чином, функцію від п змінних можна описати сумою максимум 2^п добутків, при цьому в кожному добутку буде по п множників. Таке формулювання особливо важливе, оскільки воно веде до реалізації даної функції з використанням стандартних вентилів.

Булева функція може реалізовуватися за допомогою електронної схеми (часто різними способами) з використанням сигналів, що представляють вхідні і вихідні змінні, і вентилів, наприклад, І, АБО і НЕ.