Тема № 6. Алгоритмы визуализации

При изучении данной темы рассматриваются следующие вопросы:

• алгоритмы визуализации: отсечения, развертки, удаления невидимых линий и поверхностей, закраски;

• способы создания фотореалистических изображений.

Вводная часть

Задача визуализации — выявление и представление структур и отношений в наборах данных, относящихся к определенной научной области (информатике, медицине) или более абстрактных наборах данных. Важнейшей задачей представления должно быть улучшение восприятия информации. Аглоритмы визуализации – по сути решают задачи отображения цифровых моделей обьектов на устрайствах вывода графической информации.

Таких алгоритмов существует множество, от самых простых, до невероятно сложных и запутанных, защищенных авторскими правами или вовсе являющихся коммерческой тайной. В данной лекции попытаемся описать простейшие алгоритмы растровой графики, такие как генерация отрезка прямой, окружности или эллипса, алгоритма закраски многоугольника или, в более общем случае, области плоскости, а так же алгоритмы удаления невидимых поверхностей.

Прежде чем перейти непосредственно к алгоритмам генерации растровых изображений, определим еще несколько понятий, которые в дальнейшем будут нам полезны.

Назовем точки 4-соседями (или "непосредственными" соседями), если у них отличается только одна из координат и притом только на 1. Назовем точки 8-соседями (или "косвенными" соседями), если у них отличается горизонтальная или вертикальная координата, но не более чем на 1. Не трудно заметить, что всякий непосредственный сосед является также и косвенным соседом. Всякая точка имеет 4 непосредственных и 8 косвенных соседей.

Р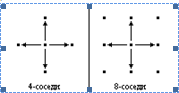 ис.1 4 и8-соседи.

Конкретные алгоритмы визуализации

Алгоритм Брезенхема посторения отрезка прямой

Представим два алгоритма Брезенхема получения 4-х и 8-ми связного представления отрезка, заданного координатами концов. Разницу между двумя этими представлениями можно увидеть на рисунке:

Р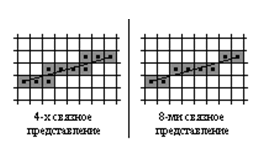 ис. 2 К алгоритму Брезенхема.

И тот и другой алгоритм используют только целочисленную арифметику, что естественно улучшает скорость работы. Различие в работе понятно и связано с разницей между 4-х и 8-ми связным представлением: в случае 4-х связности на каждом шаге мы изменяем на единицу только одну из координат текущей точки, а в случае 8-ми связности мы можем менять сразу и вертикальную и горизонтальную координаты текущей точки, но снова не более чем на единицу.

Удаление невидимых плоскостей, отсечение линий

Задача удаления невидимых линий и поверхностей продолжает оставаться центральной в машинной графике. От эффективности алгоритмов, позволяющих решить эту задачу, зависят качество и скорость построения трехмерного изображения.

Для построения правильного изображения трехмерных объектов необходимо уметь определять, какие части объектов (ребра, грани) будут видны при заданном проектировании, а какие будут закрыты другими гранями объектов. В качестве возможных видов проектирования традиционно рассматриваются параллельное и центральное (перспективное) проектирования.

К решению задачи удаления невидимых линий и поверхностей можно выделить два основных подхода.

Первый подход заключается в определении для каждого пикселя того объекта, который вдоль направления проектирования является ближайшим к нему.

Второй подход заключается в непосредственном сравнении объектов друг с другом для выяснения того, какие части каких объектов будут являться видимыми.

Отсечение нелицевых граней.

Самым первым алгоритмом, предназначенным для удаления невидимых линий был алгоритм Робертса. Сначала в нем отбрасываются все ребра, обе определяющие грани которых являются нелицевыми. Следующим шагом является проверка оставшихся ребер со всеми гранями многогранника на закрывание.

Возможны следующие случаи :

грань не закрывает ребро;

грань полностью закрывает ребро;

грань частично закрывает ребро (в этом случае ребро разбивается на несколько частей, из к-рых видимыми являются не более двух)

Алгоритм Аппеля. Этот алгоритм основан на понятии количественной невидимости точки, как кол-ва лицевых граней, ее закрывающих. Точка является видимой только в том случае, если ее количественная невидимость = 0.

Метод Z-буфера. Одним из самых простых алгоритмов удаления невидимых граней и поверхностей является метод z-буфера (буфера глубины). В силу крайней простоты этого метода часто встречаются его аппаратные реализации.

Данный метод работает исключительно в пространстве картинной плоскости и не требует никакой предварительной обработки.

Метод W-буфера.

Данный метод является простым усовершенствованием Z-буфера. Различие состоит в том, что в буфере вместо значения глубины мы храним величину, обратную величине глубины. Благодаря этому количество расчетов сокращается.

Алгоритмы упорядочения.

Подход заключается в таком упорядочении граней, чтобы при их выводе в этом порядке получалось корректное изображение. Для этого необходимо, чтобы более дальние грани выводились раньше, чем более близкие.

Метод сортировки по глубине.

Наиболее простым подходом к упорядочиванию граней является их сортировка по минимальному расстоянию до картинной плоскости (вдоль направления проектирования) с последующим выводом их в порядке приближения.

Этот метод великолепно работает для ряда сцен, включая, например, построение изображения нескольких непересекающихся достаточно простых тел. Возможны случаи, когда просто сортировка по расстоянию до картинной плоскости не обеспечивает правильного упорядочения граней.

Метод построчного сканирования. Вместо того, чтобы решать задачу удаления невидимых граней для проекций объектов на картинную плоскость, сведем ее к серии простых одномерных задач. Все изображение на картинной плоскости можно представить как ряд горизонтальных (вертикальных) линий пикселей.

Алгоритмы «закраски»

Алгоритм закраски многоугольников.

Задача "закраски" многоугольника заключается в инициализации всех его внутренние точки.

Наиболее простой, но и наиболее медленный алгоритм, решающий эту задачу состоит в том, чтобы проверить все точки на принадлежность многоугольнику.

Еще один вариант решения задачи, это алгоритм сканирования строк. Последовательно проходим все горизонтальные линии плоскости, и находим отрезки на прямой, внутренние для многоугольника. Для данного алгоритма достаточно искать только точки пересечения сканирующей линии с ребрами многоугольника.