5.2. Линии влияния усилий – изгибающих моментов в заданном сечении.

Алгоритм построения линии влияния внутреннего изгибающего момента:

а) В расчетной схеме необходимо врезать шарнир по моменту в заданном сечении, в результате чего диск, которому принадлежит это сечение, разделяется на два диска.

б) На каждый из двух полученных дисков в заданном сечении прикладываем по единичному моменту.

в) Сумму углов, образованных в результате поворота полученных дисков относительно оси балки под действием единичных моментов, приравниваем единице и строим схему возможных перемещений по очереди для каждого диска балки.

5.2.1. Построение линии влияния и определение по ней значения изгибающего момента в сечении k.

В сечении K прикладываем на диск 2–K единичный момент против часовой стрелки, а на диск K–5 – по часовой стрелке (рис. 1.34). В результате этого врезанный шарнир по моменту в сечении K должен переместиться вверх, но при условии, что оба диска 2–K и K–5 могут одновременно повернуться в шарнире.

Для начала рассмотрим диск 2–K, имеющий по концам (т. 2 и K) шарниры по моменту и опирающийся по длине в т. 3 на одностержневую приставную вертикальную связь, разрешающую поворот диска относительно этой точки. Предположим, что в т. K диск 2–K переместится вверх под действием единичного момента, при этом он должен пройти через т. 3. Отсюда по двум точкам можно построить перемещение диска 2–K. В этом случае т. 2 диска 2–K окажется в нижней части линии влияния.

Теперь рассмотрим диск K–5, имеющий на одном конце (т. K) шарнир по моменту, а на другом (т. 5) – шарнир по поперечной силе (ползун), а также опирающийся по длине в т. 4 на одностержневую приставную вертикальную связь, разрешающую поворот диска относительно этой точки. Предположим, что в т. K диск K–5 переместится вверх под действием единичного момента, при этом он должен пройти через т. 4. Отсюда по двум точкам можно построить перемещение диска K–5. Таким образом, т. 5 диска K–5 переместится вниз.

Так как оба диска 2–K и K–5 могут одновременно повернуться (изменить свое первоначальное положение), то врезанный шарнир по моменту в сечении K действительно переместится вверх, а диски 2–K и K–5 займут положения, описанные выше.

Рассмотрим диск 1–2, имеющий на одном конце (т. 1) шарнирно-неподвижную опору, разрешающую поворот диска относительно этой точки, а на другом (т. 2) соединяющийся с диском 2–K при помощи шарнира по моменту, который разрешает поворот относительно этой точки любого из двух дисков. Диск 1–2 повернется относительно т. 1 вследствие того, что т. 2 уже изменила свое первоначальное положение. Соединив т. 1 с уже отложенной для диска 2–K ординатой в т. 2, построим перемещение диска 1–2.

Диск 6–7 не изменит своего положения благодаря подвижной заделке в т. 7, воспринимающей вертикальные перемещения и поворот диска относительно точки расположения опорной связи.

Рассмотрим диск 5–6, имеющий на одном конце (т. 5) шарнир по поперечной силе (ползун), разрешающий вертикальное перемещение в шарнире концов соединяющихся в этой точке дисков, а на другом (т. 6) соединяющийся с диском 6–7 при помощи шарнира по моменту, который разрешает поворот относительно этой точки любого из двух дисков. Диск 5–6 должен переместиться параллельно диску K–5 (см. ^* на стр. 24), т. е. т. 5 диска 5–6 будет располагаться в верхней части линии влияния, а т. 6 останется на прежнем месте (диск повернется в шарнире).

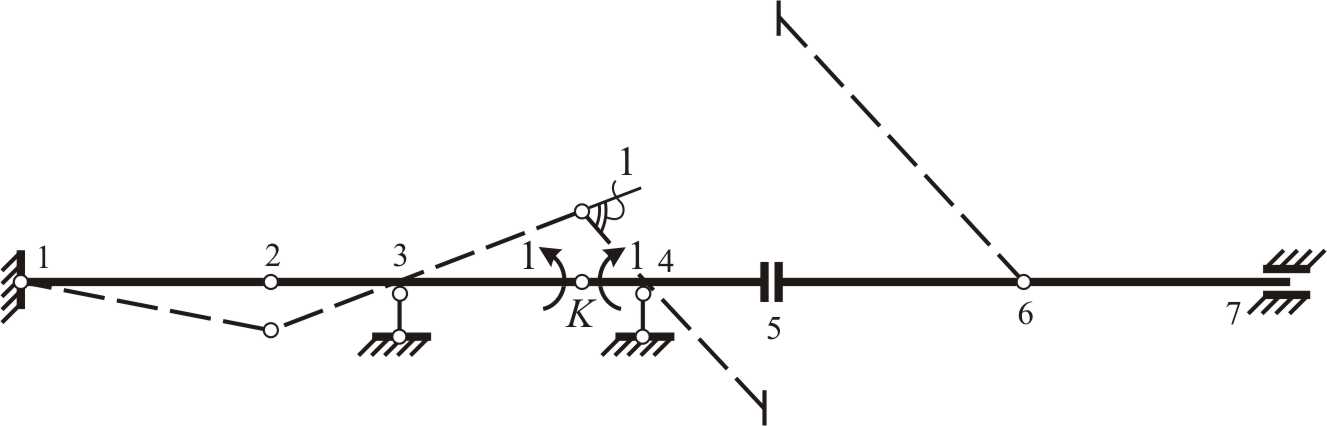
Рис. 1.34

Линия влияния имеет ненулевые участки в пределах сосредоточенной силы , приложенной в т. 8, распределенной нагрузки q на участке 2–13 и изгибающего момента , приложенного в т. 9.

В соответствии с формулой (1.1) необходимо вычислить:

1) ординаты на линии влияния по концам приложения распределенной нагрузки q ( и ), и затем площадь на участке 2–13 между этими ординатами ( );

2) ординату на линии влияния в точке приложения сосредоточенной силы ( );

3) тангенс угла наклона к оси балки линии влияния под изгибающим моментом ( ).

1) В соответствии с п. 5.2в: .

Пусть , тогда . Зная расстояния между т. 3 и K и между т. K и 4, а также, принимая и ^, найдем ординату на линии влияния в т. K, как произведение тангенса угла наклона на прилежащую сторону прямоугольного треугольника, т. е.

.

Таким образом, ; .

Зная и длины участков и можно найти ординаты в т. 2 и 13:

; .

На участке 2–13 между ординатами и имеем два треугольника (один треугольник расположен в нижней части на участке 2–3, а другой – в верхней части на участке 3–13), площадь каждого из них находится как половина произведения основания на высоту, т. е.

; .

2) Из подобия треугольников следует, что

или ,

где и – ординаты на линии влияния соответственно в т. 8 и 2;

– длина диска 1–8; – длина диска 1–2.

3) Диски K–5 и 5–6 после перемещения останутся параллельными друг другу, поэтому (соответственные углы при параллельных прямых), а значит .

Подставляя полученные данные (рис. 1.35) в формулу (1.1), получим:

• произведение взято с отрицательным знаком, так как распределенная нагрузка , приложенная на участке 2–3, направлена вниз, а соответствующий ей участок площадью на линии влияния расположен в нижней части;

• произведение взято с положительным знаком, так как распределенная нагрузка , приложенная на участке 3–13, направлена вниз, а соответствующий ей участок площадью на линии влияния расположен в верхней части;

• произведение взято с отрицательным знаком, так как сосредоточенная сила , приложенная в т. 8, направлена вниз, а ордината под этой силой на линии влияния расположена в нижней части;

• произведение взято с положительным знаком, так как внешний изгибающий момент , приложенный в т. 9, действует против часовой стрелки, а диск 5–6 под этим моментом поворачивается относительно оси балки по часовой стрелке.

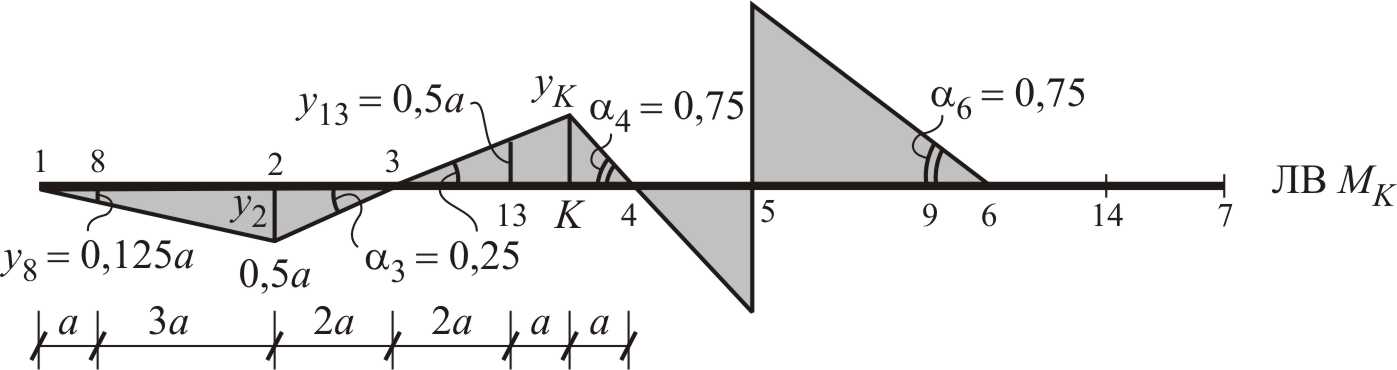
Рис. 1.35