Задания для решения в аудитории
1. Решить задачу линейного программирования графическим методом.
,
.
2. Решить задачу линейного программирования графическим методом.
,
.
1.3.1. Графический метод решения задач линейного программирования с переменными
Графическим
методом решаются задачи линейного
программирования, записанные в
каноническом виде и удовлетворяющие
условию
,
где
-
число неизвестных системы ограничений,
- ранг системы ограничений.
Для этого задача, записанная в каноническом виде методом Жордана – Гаусса приводится к стандартному виду с двумя переменными.
Пример 6. Решить задачу линейного программирования графическим методом.
,
.
Решение. Из коэффициентов уравнений системы ограничений и целевой функции составим расширенную матрицу и методом Жордана – Гаусса приведем ее к разрешенному виду.
Строки |
|
|
|
|
|
|
|
-1 |
1 |
1 |
2 |
-3 |
4 |
|
1 |
1 |
4 |
1 |
-8 |
3 |
|
0 |
1 |
1 |
0 |
-4 |
-4 |
|
-1 |
-1 |
1 |
3 |
7 |
0 |
Выберем
разрешающий элемент первой строки,
например
.
Выполним следующие действия:
,
,
.
Строки |
|
|
|
|
|
|
|
-1 |
1 |
1 |
2 |
-3 |
4 |
|
2 |
0 |
3 |
-1 |
-5 |
-1 |
|
1 |
0 |
0 |
-2 |
-1 |
-8 |
|
-2 |
0 |
2 |
5 |
4 |
4 |
Во
второй строке в качестве разрешающего
элемента выберем, например
.
Выполним следующие действия:
,
.
Строки |
|
|
|
|
|
|
|
-5/3 |
1 |
0 |
7/3 |
-4/3 |
13/3 |
|
2 |
0 |
3 |
-1 |
-5 |
-1 |
|
1 |
0 |
0 |
-2 |
-1 |
-8 |
|
-5/3 |
0 |
0 |
17/6 |
11/3 |
7/3 |
В
третьей строке в качестве разрешающей
удобно выбрать переменную
.
Выполним следующие действия:
,
,
.
Строки |
|
|
|
|
|
|
|
0 |
1 |
0 |
-1 |
-3 |
-9 |
|
0 |
0 |
3 |
3 |
-3 |
15 |
|
1 |
0 |
0 |
-2 |
-1 |
-8 |
|
0 |
0 |
0 |
-1/2 |
2 |
-11 |
Разделим вторую строку на три, а четвертую умножим на два.
Строки |
|
|
|
|
|
|
|
0 |
1 |
0 |
-1 |
-3 |
-9 |
|
0 |
0 |
1 |
1 |
-1 |
5 |
|
1 |
0 |
0 |
-2 |
-1 |
-8 |
|
0 |
0 |
0 |
-1 |
4 |
-22 |
С помощью последней таблицы составим систему ограничений и целевую функцию.
,
.
Переменные , и входят в уравнения со знаком плюс, поэтому их можно отбросить, а знак заменить знаком .
,
.
Последняя задача является задачей линейного программирования с двумя переменными и может быть решена графическим методом.
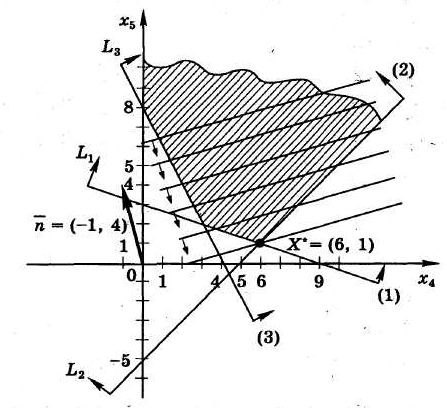
Для
того чтобы получить оптимальное решение
исходной задачи используется система
ограничений в разрешенном виде (из
последней таблицы) и точка
.
Оптимальное
значение целевой функции равно
и достигается в точке
.