Развернутая форма игры.

При таком задании игры больше внимания уделяется порядку ходов и той информации, которая при этом открывается игроку. Начнем с простейших, т.н. позиционных игр, или игр с полной информацией. Главное здесь - дерево игры; это направленный граф без циклов с выделенной вершиной - корнем. Стрелки идут в направлении от корня. Вершины дерева изображают позиции игры, места, где какие-то игроки должны выбрать ход - одну из стрелок, выходящую из этой вершины. Поэтому у каждой (нетерминальной) вершины стоит метка того игрока, который делает ход (говорят еще - контролирует эту вершину). В терминальных вершинах (где игра заканчивается) стоит вектор выигрышей игроков.

Всем известна игра в крестики-нолики на доске 3 х 3. В начальной позиции у первого игрока 9 ходов, затем у второго по 8 ходов в каждой из этих 9 позиций, затем у первого игрока по 7 ходов в каждой из получающихся 72 позиций, и т.д. Рассмотрим фрагмент дерева игры.

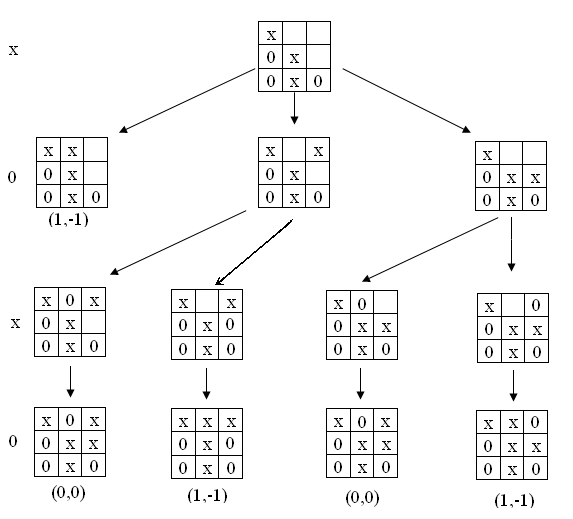
Рисунок 1 Фрагмент дерева игры «крестики-нолики»

В начальной позиции фрагмента игроки сделали по 3 хода. Очередь хода за «крестиками». Позиции дерева расположены уровнями. Очередь хода на каждом уровне отмечена в левой стороне рисунка.

Скажем кратко об этом. Примитивные понятия: множество X чистых исходов, множество Д(АГ) лотерейных исходов, и - конечное множество состояний природы. Действие -это отображение / : Л — > А(Х); множество их обозначается С. На С задано предпочтение :<, которое удовлетворяет тем же аксиомам: слабый порядок, независимость и непрерывность. Тогда :< представляется обобщенной ожидаемой полезностью вида Х^еп иш(]'(и}}. Фактически это уже было доказано.

Новое появляется, если мы потребуем, чтобы полезности иш не зависели от состояния природы и. Например, этого можно добиться, добавив к уже упомянутым трем аксиомам аксиому монотонности. Чтобы ее сформулировать, заметим, что постоянные лотереи позволяют индуцировать на симплекс &(Х) предпочтение ^ с множества £, которое изображается той же буквой.

4. Аксиома монотонности. Пусть / и g - два действия, и для любого о/ G Г2 f(&} >: g(^), тогда / >: g. Как легко понять, в этом случае предпочтения на Д(^), индуцированные функциями иш, не зависят от и. Из единственности полезности Н-М следует, что иш = тг(и;)[/ + а(и;), и тт(си) > 0. Нормируя тг, можно считать, что Y^u 'n(jj] — 1? т-е- является требуемой вероятностью на Л. Полезность на £ в этом случае представляется функцией / н-> f^ U(f(u))d7v(u;).

Рациональность игроков

Представим себе идеального игрока, который в любой игровой ситуации принимает наилучшее решение. Он обеспечивает себе наибольший выигрыш, по сравнению с любым другим игроком, который от него отличается. Если бы мы могли описать поведение такого игрока, то мы смогли бы ответить на вопрос: как надо играть, и решили бы задачу теории игр. К сожалению, анализ даже весьма простых игр, таких как «чет-нечет», показывает, что идеальный игрок не более чем утопия. Тем не менее, вопрос «как играть» остается, и как-то его надо решать. Тут на сцене появляется игрок, к которому предъявляются следующие требования. Он должен на основе всех своих знаний об игре и всей имеющейся информации о ее ходе выжать из игры максимум возможного и принять решение, которое в каком то смысле будет оптимальным. Такое довольно туманное определение соответствует понятию рационального игрока.