4.3. Основные виды сравнений в ахд
Сравнение – научный метод познания, когда изучаемое явление сопоставляется с уже известным с целью определения общих черт или различий м/у ними. Исп-ся для опред-ия общего и специфического в эконом-их явлениях, изучения тенденций и закономерностей развития. Обязат-ым условием сравнения явл-ся сопоставимость показателей (их кач-ая однородность).
Осн. направления сравнений:
1)сопоставление факт. данных с план-ми для определ-ия степени выполнения заданий (Факт/План);
2)сопост-ие факт. показателей отчет-го периода с аналог-ми показ-ми прошлых лет для оценки динамики и тенденции развития процесса (Факт/Фактпрошлого);
3)сравн-ие показателей анализируемого предпр-ия со средними аналог-ми показ-ми по отрасли для выявления его доли и места на рынке (Факт/Средний);
4)сопост-ие показателей анализир-го предпр-ия с высокорентаб-ми по аналог-ым показ-лям для выявления неиспольз-ых резервов роста произв-ва (Факт/Лучший);
5)сопост-ие рез-тов деят-ти до и после примен-ия некоторого мероприятия для определ-ия колич-го влияния факторов и резерва повыш-ия эффект-ти работы (До/После);
6)сопост-ие факт. показ-лей с нормативами для контроля затрат ресурсов и эффект-ти их использ-ия (Факт/Норма);
7)сравн-ие разл-ых вариантов управл-их решений для выбора оптим-го.
8)сопоставл-е параллельных и динамических рядов для изуч-я взаимосвязи илсслед-х пок-лей
Виды сравнения:
горизонт-ый анализ – опред-ие абсолютных и относит-ых отклонений факт-го уровня показ-ля от план-го (базового, среднего, прошлого или будущего периода);
вертикальный а-з – определ-ие состава итоговых показателей, доли, удельного веса частей в результирующем показателе;
трендовый а-з – сравнение за несколько лет и опред-ие динамики показателя;
одномерный сравнит-ый а-з – сопоставление показателей одного объекта или нескольких объектов по одному показателю;
многомерный сравнит-ый а-з – сравн-ие результатов деят-ти нескольких хоз-их субъектов по широкому кругу показателей.
Факторный анализ (фа): задачи, классификация факторов, виды моделей, правила их исп-ия и преобразования.
Основной среди применяемых методик анализа является методика ФА. ФА – методика комплексного и системного изучения и измерения воздействия факторов на результат.
Основные задачи ФА: 1)Отбор факторов для а-за исследуемых показ-лей; 2)Классиф-ия и систематизация факторов; 3)Моделир-ие взаимосвязей м/у результативными и факторными показ-ми; 4)Расчет влияния факторов и оценка роли каждого из них; 5)практ-ое применение факторных расчетов.
Классиф-ия факторов:
Признак |
Вид факторов |
По природе |
Природно-климатические, соц-эконом-ие, производственно-экономич |
По взаимодействию |
Основные, второстепенные |
По влиянию |
Объективные, субъективные |
По месту возникновения |
Внутренние, внешние |
По распространенности |
Общие, специфические |
По времени действия |
Постоянные, временные |
По характеру действия |
Интенсивные, экстенсивные |
По направлению действия |
Прямые, косвенные |
По свойствам |
Количественные, качественные |
По составу |
Простые (элементные), сложные (комбинированные) |
По результату |
Положительные, отрицательные |
По возможности измерения |
Измеримые (параметрические), неизмеримые (непараметрические) |
По соподчиненности (иерархи) |
Первого, второго, третьего порядка и т.д. |
В ФА различают модели детерминированные (функциональные) и стохастические (корреляционные). С помощью детерминированных факторных моделей исследуется функциональная связь между результативным показателем (функцией) и факторами (аргументами).
При моделир-ии детерминир-ых факторных систем необходимо выполнять ряд требований:
1. Факторы, включаемые в модель и сами модели должны реально существовать, а не быть абстрактными.
2. Факторы, которые входят в систему, должны быть не только необходимыми элементами формулы, но и находиться в причинно-следственной связи с изучаемыми показателями.
3. Все показ-ли факторной модели д.б. колич-но измеримыми, т.е. должны иметь ед-цу измерения и необх-ую информ-ую обеспеч-ть.
4. Сумма влияния отдельных факторов должна равняться общему приросту результативного показателя.
В ФА выделяют следующие наиболее часто встречающиеся типы факторных моделей:
аддитивные модели (y=
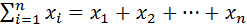)мультипликативные модели (y=
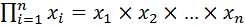)кратные модели (y=
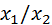)смешанные (комбинированные) модели – это сочетание различных вариантов предыдущих моделей (y=
).
При построении детерминир-ых факторных моделей можно исходную модель заменить более наглядной путем след-их преобразований:
расчленение – один или несколько факторов дробятся на сомножители (составные эл-ты): у=a*b=a*c*d или у=a+b=a+c+d
удлинение – замена одного или нескольких факторов на сумму однородных показателей: (
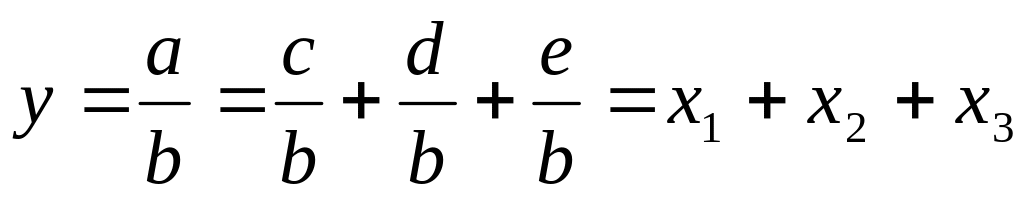)формальное разложение – удлинение знаменателя ф-лы путем замены одного или нескольких факторов на сумму или произведение показателей (y=
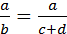)расширение – умножение числителя и знаменателя дроби на один или несколько новых показателей (y=
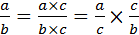)сокращение – деление числителя и знаменателя дроби на один и тот же показатель (y=
)
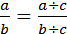Таким образом, результативные показатели могут быть разложены на составные элементы (факторы) различными способами и представлены в виде различных типов факторных моделей. Выбор способа моделирования зависит от объекта исследования и от поставленной цели анализа.