12. Понятие ассоциативной памяти и задача распознавания образов.

Динамический процесс последовательной смены состояний нейронной сети Хопфилда завершается в некотором стационарном состоянии, являющемся локальным минимумом энергетической функции E(S). Невозрастание энергии в процессе динамики приводит к выбору такого локального минимума S, в бассейн притяжения которого попадает начальное состояние (исходный, пред'являемый сети образ) S0. В этом случае также говорят, что состояние S0 находится в чаше минимума S.

При последовательной динамике в качестве стационарного состояния будет выбран такой образ S, который потребует минимального числа изменений состояний отдельных нейронов. Поскольку для двух двоичных векторов минимальное число изменений компонент, переводящее один вектор в другой, является расстоянием Хемминга r H(S,S0), то можно заключить, что динамика сети заканчивается в ближайшем по Хеммингу локальном минимуме энергии.

Пусть состояние S соответствует некоторому идеальному образу памяти. Тогда эволюцию от состояния S0 к состоянию S можно сравнить с процедурой постепенного восстановления идеального образа S по его искаженной (зашумленной или неполной) копии S0. Память с такими свойствами процесса считывания информации является ассоциативной. При поиске искаженные части целого восстанавливаются по имеющимся неискаженным частям на основе ассоциативных связей между ними.

Ассоциативный характер памяти сети Хопфилда качественно отличает ее от обычной, адресной, компьютерной памяти. В последней извлечение необходимой информации происходит по адресу ее начальной точки (ячейки памяти). Потеря адреса (или даже отного бита адреса) приводит к потере доступа ко всему информационному фрагменту. При использовании ассоциативной памяти доступ к информации производится непосредственно по ее содержанию, т.е. по частично известным искаженным фрагментам. Потеря части информации или ее информационное зашумление не приводит к катастрофическому ограничению доступа, если оставшейся информации достаточно для извлечения идеального образа.

Поиск идеального образа по имеющейся неполной или зашумленной его версии называется задачей распознавания образов.

13. Архитектура и принципы работы нейронной сети дап (двунаправленная ассоциативная память). Емкость сети дап. Модификации сети дап.

Д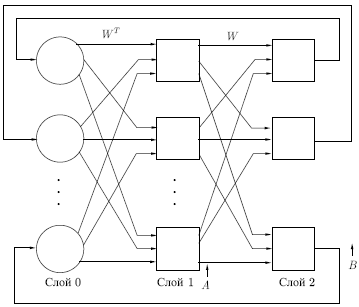 вунаправленная ассоциативная память (ДАП) является гетероассоциативной; входной вектор поступает на один набор нейронов, а соответствующий выходной вектор появляется на другом наборе нейронов. Как и сеть Хопфилда, ДАП способна к обобщению, вырабатывая правильные реакции, несмотря на искаженные входы. Кроме того, могут быть реализованы адаптивные версии ДАП, выделяющие эталонный образ из зашумленных экземпляров. Эти возможности сильно напоминают процесс мышления человека и позволяют искусственным нейронным сетям приблизиться к моделированию естественного мозга. На рис. 10.1 приведена базовая конфигурация ДАП. Она выбрана таким образом, чтобы подчеркнуть сходство с сетями Хопфилда и предусмотреть увеличения количества слоев. На рис. 10.1 входной вектор обрабатывается матрицей весов сети, в результате чего вырабатывается вектор выходных сигналов нейронов Вектор затем обрабатывается транспонированной матрицей весов сети, которая вырабатывает новые выходные сигналы, представляющие собой новый входной вектор Процесс повторяется до тех пор, пока сеть не достигнет стабильного состояния, в котором ни вектор , ни вектор не изменяются. Заметим, что нейроны в слоях 1 и 2 функционируют, как и в других парадигмах, вычисляя сумму взвешенных входов и вычисляя по ней значение функции активации

Как и сети Хопфилда, ДАП имеет ограничения на максимальное количество ассоциаций, которые она может точно воспроизвести. Если этот лимит превышен, сеть может выработать неверный выходной сигнал, воспроизводя ассоциации, которым не обучена.

Б. Коско получил оценки, в соответствии с которыми количество запомненных ассоциаций не может превышать количества нейронов в меньшем слое. Для этого емкость памяти должна быть максимизирована посредством специального кодирования, при котором количество компонент со значениями равно количеству компонент со значениями в каждом биполярном векторе. Эта оценка оказалась слишком оптимистичной. Е.Г. Рознер показал, что оценка емкости сетей Хопфилда может быть легко обобщена для ДАП. Можно показать, что если векторов выбраны случайно и представлены в указанной выше форме, и если меньше чем ), где — количество нейронов в наименьшем слое, тогда все запомненные образы, за исключением "малой части", могут быть восстановлены.Непрерывная ДАП. В предшествующем нейроны в слоях 1 и 2 рассматривались как синхронные; каждый нейрон обладает памятью, причем все нейроны изменяют состояния одновременно под воздействием импульса от центральных часов. В асинхронной системе любой нейрон свободен изменять состояние в любое время, когда его вход предписывает это сделать. Кроме того, при определении функции активации нейрона использовался простой порог, образуя разрывность передаточной функции нейронов. Как синхронность функционирования, так и разрывность функций являются биологически неправдоподобными и совсем необязательными; непрерывные асинхронные ДАП отвергают синхронность и разрывность, но функционируют в основном аналогично дискретным версиям. Может показаться, что такие системы должны быть нестабильными. Показано, что непрерывные ДАП являются стабильными (однако для них справедливы ограничения емкости, указанные ранее). С. Гроссберг показал, что сигмоида является оптимальной функцией активации благодаря ее способности усиливать низкоуровневые сигналы и в то же время сжимать динамический диапазон нейронов. Непрерывная ДАП может иметь сигмоидальную функцию с величиной , близкой к единице, и создавать тем самым нейроны с плавной и непрерывной реакцией, во многом аналогичной реакции их биологических прототипов. Адаптивная ДАП. В версиях ДАП, рассматриваемых до сих пор, весовая матрица вычисляется в виде суммы произведений пар векторов. Такие вычисления полезны, поскольку они демонстрируют функции, которые может выполнять ДАП. Однако это определенно не тот способ, посредством которого производится определение весов нейронов мозга. Адаптивная ДАП изменяет свои веса в процессе функционирования. Это означает, что подача на вход сети обучающего набора входных векторов заставляет ее изменять энергетическое состояние до получения резонанса. Постепенно кратковременная память превращается в долговременную память, настраивая сеть в ходе ее функционирования. В процессе обучения векторы подаются на слой , а ассоциированные векторы — на слой Один из них или оба вектора могут быть зашумленными версиями эталона; сеть обучается исходным векторам, свободным от шума. В этом случае она извлекает сущность ассоциаций, обучаясь эталонам, хотя "видела" только зашумленные аппроксимации. Так как доказано, что непрерывная ДАП является стабильной независимо от значения весов, ожидается, что медленное изменение ее весов не должно нарушить этой стабильности.

Простейший обучающий алгоритм использует правило Хэбба, в котором изменение веса пропорционально уровню активации его нейрона- источника и уровню активации нейрона-приемника. Конкурирующая ДАП. Во многих конкурирующих нейронных системах наблюдаются некоторые виды конкуренции между нейронами. В нейронах, обрабатывающих сигналы от сетчатки, латеральное торможение приводит к увеличению выхода наиболее высокоактивных нейронов за счет соседних. Такие системы увеличивают контрастность, поднимая уровень активности нейронов, подсоединенных к яркой области сетчатки, и в то же время еще более ослабляя выходы нейронов, подсоединенных к темным областям. В ДАП конкуренция реализуется с помощью взаимного соединения нейронов внутри каждого слоя посредством дополнительных связей. Веса этих связей формируют другую весовую матрицу с положительными значениями элементов главной диагонали и отрицательными значениями остальных элементов. Теорема Кохонена-Гроссберга показывает, что такая сеть является безусловно стабильной, если весовые матрицы симметричны. На практике сети обычно стабильны даже в случае отсутствия симметрии весовых матриц. Однако неизвестно, какие особенности весовых матриц могут привести к неустойчивости функционирования сети.