3. Алгоритм обучения многослойного персептрона с учителем.

«алгоритм обратного распространения ошибки» или алгоритм Румельхарта-Хинтона-Вильямса. Данный алгоритм относится к алгоритмам обучения с учителем. Для обучения сети, так же как и для однослойного персептрона, необходимо иметь множество пар векторов {x^s, d^s}, s = 1…S, где {x^s} = {x¹,…, х^s} – множество входных векторов x, {d^s} = {d¹,…, d^s} – множество эталонов выходных векторов. Совокупность пар {x^s, d^s} образуют обучающее множество. Количество элементов S в обучающем множестве должно быть достаточным для обучения сети, чтобы под управлением алгоритма сформировать набор параметров сети, дающий нужное отображение x → y. Количество пар в обучающем множестве не регламентируется. Если элементов слишком много или мало, сеть не обучится и не решит поставленную задачу. Выберем один из векторов х и подадим его на вход сети. На выходе получится некоторый вектор y. Тогда ошибкой сети можно считать Еs = ||d^s – y^s|| для каждой пары (x^s, d^s). Алгоритмом обучения, минимизируется суммарная квадратичная ошибка, которая имеет вид:

Где j – число нейронов в выходном слое сети. Задача обучения ставится так: подобрать такие значения параметров сети, чтобы ошибка Е была минимальной для данного обучающего множества. Большая часть методов обучения итерационные. Параметрам сети (весовым коэффициентам и пороговым уровням) присваиваются малые начальные значения. Затем параметры изменяются так, чтобы ошибка Е убывала. Изменения продолжаются до тех пор, пока ошибка не станет достаточно малой. Ошибка Е нейронной сети является функцией параметров сети, то есть мы имеем некоторую функцию Е(P), где P – параметр сети. Параметр Р является вектором:

Где W — вектор, компоненты которого все весовые коэффициенты сети. Таким образом, если считать обучающее множество заданным, то ошибка сети зависит только от вектора параметров Е = Е(P). При обучении на каждой итерации будем корректировать параметры в направлении антиградиента Е:

В теории оптимизации доказано, что такой алгоритм обеспечивает сходимость к одному из локальных минимумов функции ошибки, при условии правильного выбора ε > 0 на каждой итерации. Такой метод оптимизации называется методом наискорейшего спуска. Коррекции необходимо рассчитывать на каждой итерации. Поэтому каждая итерация требует расчета компонент градиента ∇E и выбора оптимального шага ε. Коррекции параметров сети необходимо рассчитывать на каждой итерации. Поэтому каждая итерация требует расчета компонент градиента ∇E и выбора оптимального шага ε.

4. Алгоритм обратного распространения.

Алгоритм обратного распространения ошибки — способ ускоренного расчета компонент градиента. Идея метода в том, чтобы представить Е в виде сложной функции и последовательно рассчитать частные производные по формуле для сложной функции. Алгоритм обратного распространения разбивается на два этапа. На первом этапе на вход сети подаётся некоторый входной вектор из обучающего множества, производится расчёт выходов нейронной сети. На втором этапе подсчитывается ошибка (δ) для каждого выхода сети и начинается её обратное распространение от выходного слоя к входному. Алгоритм обратного распространения опирается на обобщение дельта-правила. Запишем частную производную суммарной квадратичной ошибки по весовым коэффициентам:

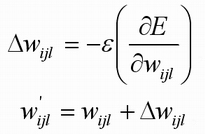
Где w^|_ijl - вес на следующей итерации обучения; w_ijl - вес на данной итерации обучения. Представим производную ошибки в виде:

Определим величину δ_jl с помощью формулы:

Данную формулу можно переписать в виде:

Поскольку для одной пары из обучающей выборки

имеем (производная квадрата переменной равна переменной умноженной на 2):

Для функции активации выходом является:

Поэтому для производной f^| получаем:

Таким образом:

Для нахождения комбинированного ввода используется обычное суммирование произведений:

Поэтому:

Рассмотрев произведение полученных производных получим:

Мы получили частную производную суммарной квадратичной ошибки от веса нейрона выходного слоя. С учётом того, что вес должен изменяться в направлении, противоположном тому, которое указывает производная поверхности ошибок, и с учётом скорости обучения ε, изменение веса для элемента должно вычисляться по формуле:

Удобной функцией активации является сигмоидальная функция:

Производная этой функции равна:

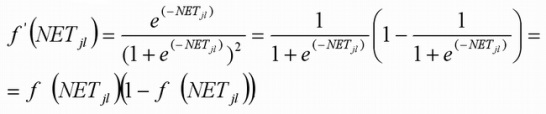
Поэтому, при использовании в качестве функции активации сигмоиды, для выходного слоя ошибку δ_jl можно записать в виде:

Указанная выше ошибка δ соответствует ошибке выходного элемента, но ошибка скрытого элемента не связана с целевым выходным значением непосредственно. Поэтому весовые значения скрытого элемента следует скорректировать пропорционально его "вкладу" в величину ошибки следующего слоя (т.е. выходного слоя в случае сети с одним скрытым слоем). В сети с одним скрытым слоем при распространении сигналов ошибок в обратном направлении ошибка каждого выходного элемента вносит свой "вклад" в ошибку каждого элемента скрытого слоя. Этот "вклад" для элемента скрытого слоя зависит от величины ошибки выходного элемента и весового коэффициента связи, соединяющей элементы. Другими словами, выходной элемент с большей ошибкой делает больший "вклад" в ошибку того элемента скрытого слоя, который связан с данным выходным элементом большим по величине весом. Для скрытого элемента ошибка вычисляется по формуле:

Если мы используем в качестве функции активации сигмоиду, предыдущую формулу можно переписать в виде (смотрите предыдущую страницу):

Изменение веса для нейрона скрытого слоя вычисляется по той же формуле, что и для нейрона выходного слоя:

Где x_i – вход нейрона данного скрытого слоя. На первой стадии происходит инициализация весов малыми случайными значениями — например, значениями из диапазона между -0.3 и +0.3. Обучение продолжается до тех пор, пока изменение средней квадратичной ошибки не окажется меньше некоторого допустимого значения при переходе от одной итерации к следующей. Например, допустимое значение 0.01 означает, что средняя квадратичная ошибка соседних итераций не должна отличаться более чем на ±0.01. Если в процессе обучения наступает момент, когда ошибка в сети попадает в рамки допустимого изменения, говорят, что наблюдается сходимость. Другим критерием окончания обучения можно считать наступление момента, когда выход для каждого учебного образца оказывается в рамках допустимого отклонения от соответствующего целевого выходного образца, либо суммарная квадратичная ошибка Е стала меньше какой-то заранее известной величины. Пошагово распишем работу алгоритма обратного распространения ошибки:

1. Присвоить всем весам всех нейронов сети небольшие произвольные значения.

2. Прочитать входной и соответствующий ему выходной образец из обучающей выборки.

3. Для входного слоя установить совокупный ввод каждого элемента равным соответствующему элементу входного вектора. Значение вывода каждого элемента установить равным вводу.

4. Для нейронов первого скрытого слоя вычислить NET и OUT.

5. Повторить шаг 4 последовательно для всех последующих скрытых слоев сети, начиная с второго скрытого слоя.

6. Для каждого нейрона выходного слоя рассчитать его онибку δ.

7. Для последнего скрытого слоя вычислить ошибку каждого нейрона δ.

8. Повторить шаг 7 последовательно для всех предыдущих скрытых слоёв, идущих до последнего скрытого.

9. Для всех слоев обновить значения весов каждого нейрона.

10. Если прошлись по всей обучающей выборке, то перейти к пункту 11, если нет, то к пункту 2.

11. Рассчитать суммарную квадратичную ошибку по выборке.

12. Если суммарная квадратичная ошибка по выборке меньше некоторого значения, то перейти к пункту 13, если нет, то к пункту 2.

13. Конец обучения сети.

5. Методы обучения сетей встречного распространения. Сжатие данных при помощи сетей встречного распространения.

Во встречном распространении объединены два хорошо известных алгоритма: самоорганизующаяся карта Кохонена и звезда Гроссберга. При этом появляются свойства, которых нет ни у одного из них в отдельности.

1. Обучение слоя Кохонена

Слой Кохонена классифицирует входные векторы в группы схожих. Это достигается с помощью такой подстройки весов слоя Кохонена, что близкие входные векторы активируют один и тот же нейрон данного слоя. Затем задачей слоя Гроссберга является получение требуемых выходов. Обучение Кохонена является самообучением, протекающим без учителя. Поэтому трудно (и не нужно) предсказывать, какой именно нейрон Кохонена будет активироваться для заданного входного вектора. Необходимо лишь гарантировать, чтобы в результате обучения разделялись несхожие входные векторы.

Если для каждого входного вектора активировался лишь один нейрон Кохонена. Это называется методом аккредитации. Его точность ограничена, так как выход полностью является функцией лишь одного нейрона Кохонена. В методе интерполяции целая группа нейронов Кохонена, имеющих наибольшие выходы, может передавать свои выходные сигналы в слой Гроссберга. Число нейронов в такой группе должно выбираться в зависимости от задачи, и убедительных данных относительно оптимального размера группы не имеется. Как только группа определена, ее множество выходов NET рассматривается как вектор, длина которого нормализуется на единицу делением каждого значения NET на корень квадратный из суммы квадратов значений NET в группе. Все нейроны вне группы имеют нулевые выходы. Метод интерполяции способен устанавливать более сложные соответствия и может давать более точные результаты. По-прежнему, однако, нет убедительных данных, позволяющих сравнить режимы интерполяции и аккредитации.

2. Обучение слоя Гроссберга

Слой Гроссберга обучается относительно просто. Входной вектор, являющийся выходом слоя Кохонена, подается на слой нейронов Гроссберга, и выходы слоя Гроссберга вычисляются, как при нормальном функционировании. Далее, каждый вес корректируется лишь в том случае, если он соединен с нейроном Кохонена, имеющим ненулевой выход. Величина коррекции веса пропорциональна разности между весом и требуемым выходом нейрона Гроссберга, с которым он соединен. В символьной записи

vijн = vijс + ß(yj - vijс)ki,

где ki - выход i-го нейрона Кохонена (только для одного нейрона Кохонена он отличен от нуля); уj - j-ая компонента вектора желаемых выходов. Первоначально ß берется равным ~0,1 и затем постепенно уменьшается в процессе обучения. Отсюда видно, что веса слоя Гроссберга будут сходиться к средним величинам от желаемых выходов, тогда как веса слоя Кохонена обучаются на средних значениях входов. Обучение слоя Гроссберга - это обучение с учителем, алгоритм располагает желаемым выходом, по которому он обучается. Обучающийся без учителя, самоорганизующийся слой Кохонена дает выходы в недетерминированных позициях. Они отображаются в желаемые выходы слоем Гроссберга.

Сеть встречного распространения может быть использована для сжатия данных перед их передачей, уменьшая тем самым число битов, которые должны быть переданы. Допустим, что требуется передать некоторое изображение. Тогда каждое подизображение является вектором, элементами которого являются пиксели, из которых состоит подизображение. Если в подизображении имеется п пикселей, то для его передачи потребуется п бит. Если допустимы некоторые искажения, то для передачи типичного изображения требуется существенно меньшее число битов, что позволяет передавать изображения быстрее. Это возможно из-за статистического распределения векторов подизображении. 

6. Основные стохастические методы обучения нейронных сетей.

Стохастические методы обучения выполняют псевдослучайные изменения величин весов, сохраняя те из них, которые ведут к улучшениям. Для обучения сети может быть использована следующая процедура:

1. Выбрать вес случайным образом и подкорректировать его на небольшое случайное значение. Предъявить множество входов и вычислить получающиеся выходы.

2. Сравнить эти выходы с желаемыми и вычислить величину разности между ними. Общепринятый метод состоит в нахождении разности между фактическим и желаемым выходами для каждого элемента обучаемой пары, возведение разностей в квадрат и нахождение их суммы. Целью обучения является минимизация этой разности, часто называемой целевой функцией.

3. Выбрать вес случайным образом и подкорректировать его на небольшое случайное значение. Если коррекция помогает (уменьшает целевую функцию), то сохранить ее, в противном случае вернуться к первоначальному значению веса.

4. Повторять предыдущие шаги до тех пор, пока сеть не будет обучена в достаточной степени.

Стохастические методы полезны как для обучения искусственных нейронных сетей, так и для получения выхода от уже обученной сети. Стохастические методы обучения приносят большую пользу, позволяя исключать локальные минимумы в процессе обучения. Но с ними также связан ряд проблем.

Использование обучения

Искусственная нейронная сеть обучается с помощью некоторого процесса, модифицирующего ее веса. Если обучение успешно, то предъявление сети множества входных сигналов приводит к появлению желаемого множества выходных сигналов. Имеется два класса обучающих методов: детерминистский и стохастический.

Детерминистский метод обучения шаг за шагом осуществляет процедуру коррекции весов сети, основанную на использовании их текущих значений, а также величин входов, фактических выходов и желаемых выходов. Обучение персептрона является примером подобного детерминистского метода.

С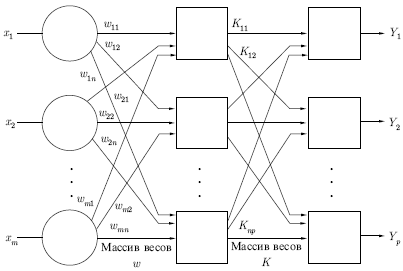 тохастические методы обучения выполняют псевдослучайные изменения величин весов, сохраняя те изменения, которые ведут к улучшениям. Чтобы показать это наглядно, рассмотрим рисунок, на котором изображена типичная сеть, где нейроны соединены с помощью весов. Выход нейрона является здесь взвешенной суммой его входов, которая преобразована с помощью нелинейной функции. Для обучения сети могут быть использованы следующие процедуры:

1. Выбрать вес случайным образом и подкорректировать его на небольшое случайное число. Предъявить множество входов и вычислить получающиеся выходы.

2. Сравнить эти выходы с желаемыми выходами и вычислить величину разности между ними. Общепринятый метод состоит в нахождении разности между фактическим и желаемым выходами для каждого элемента обучаемой пары, возведение разностей в квадрат и нахождение суммы этих квадратов. Целью обучения является минимизация этой разности, часто называемой целевой функцией.

3. Выбрать вес случайным образом и подкорректировать его на небольшое случайное значение. Если коррекция помогает (уменьшает целевую функцию), то сохранить ее, в противном случае вернуться к первоначальному значению веса.

4. Повторять шаги с 1 по 3 до тех пор, пока сеть не будет обучена в достаточной степени.

Искусственные нейронные сети могут обучаться, по существу, тем же способом при помощи случайной коррекции весов. Вначале делаются большие случайные коррекции с сохранением только тех изменений весов, которые уменьшают целевую функцию. Затем средний размер шага постепенно уменьшается, и глобальный минимум в конце концов достигается.

Эта процедура весьма напоминает отжиг металла, поэтому для ее описания часто используют термин "имитация отжига". В металле, который нагрет до температуры, превышающей его точку плавления, атомы находятся в сильном беспорядочном движении. Как и во всех физических системах, атомы стремятся к состоянию минимума энергии (единому кристаллу, в данном случае), но при высоких температурах энергия атомных движений препятствует этому. В процессе постепенного охлаждения металла возникают все более низкоэнергетические состояния, пока, в конце концов, не будет достигнуто самое малое из возможных состояний, глобальный минимум. В процессе отжига распределение энергетических уровней описывается следующим соотношением:

где — вероятность того, что система находится в состоянии с энергией ; — постоянная Больцмана; — температура по шкале Кельвина.

При высоких температурах приближается к единице для всех энергетических состояний. Таким образом, высокоэнергетическое состояние почти столь же вероятно, как и низкоэнергетическое. По мере уменьшения температуры вероятность высокоэнергетических состояний уменьшается по отношению к низкоэнергетическим. При приближении температуры к нулю становится весьма маловероятным, чтобы система находилась в высокоэнергетическом состоянии.

Методы обучения:

1. Больцмановское обучение

2. Обучение Коши

3. Метод искусственной теплоемкости

6. Больцмановское обучение нейронных сетей.

Этот стохастический метод непосредственно применим к обучению искусственных нейронных сетей:

1. Определить переменную , представляющую искусственную температуру. Придать большое начальное значение.

2. Предъявить сети множество входов и вычислить выходы и целевую функцию.

3. Дать случайное изменение весу и пересчитать выход сети и изменение целевой функции в соответствии со сделанным изменением веса.

4. Если целевая функция уменьшилась (улучшилась), то сохранить изменение веса.

Если изменение веса приводит к увеличению целевой функции, то вероятность сохранения этого изменения вычисляется с помощью распределения Больцмана:

где — вероятность изменения в целевой функции; — константа, аналогичная константе Больцмана, выбираемая в зависимости от задачи; — искусственная температура.

Выбирается случайное число из равномерного распределения от нуля до единицы. Если больше, чем , то изменение сохраняется, в противном случае величина веса возвращается к предыдущему значению. Это позволяет системе делать случайный шаг в направлении, портящем целевую функцию, и дает ей тем самым возможность вырываться из локальных минимумов, где любой малый шаг увеличивает целевую функцию.

Для завершения больцмановского обучения повторяют шаги 3 и 4 для каждого из весов сети, постепенно уменьшая температуру , пока не будет достигнуто допустимо низкое значение целевой функции. В этот момент предъявляется другой входной вектор, и процесс обучения повторяется. Сеть обучается на всех векторах обучающего множества, с возможным повторением, пока целевая функция не станет допустимой для всех них.

Величина случайного изменения веса на шаге 3 может определяться различными способами. Например, подобно тепловой системе, весовое изменение может выбираться в соответствии с гауссовским распределением:

где — вероятность изменения веса на величину , — искусственная температура.

Так как требуется величина изменения веса , а не вероятность изменения веса, имеющего величину , то метод Монте-Карло может быть использован следующим образом:

1. Найти кумулятивную вероятность, соответствующую Это есть интеграл от в пределах от 0 до 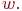Поскольку в данном случае не может быть проинтегрирована аналитически, она должна интегрироваться численно, а результат необходимо затабулировать.

2. Выбрать случайное число из равномерного распределения на интервале (0,1). Используя эту величину в качестве значения , найти в таблице соответствующее значение для величины изменения веса.

Свойства машины Больцмана широко изучены. Скорость уменьшения температуры должна быть обратно пропорциональна логарифму времени, чтобы была достигнута сходимость к глобальному минимуму. Скорость охлаждения в такой системе выражается следующим образом:

где — искусственная температура как функция времени; — начальная искусственная температура; — искусственное время.

Этот разочаровывающий результат предсказывает очень медленную скорость охлаждения (и вычислений). Вывод подтвержден и экспериментально. Машины Больцмана часто требуют для обучения очень большого ресурса времени.

6. Обучение нейронных сетей методом Коши.

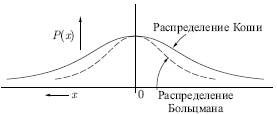Рис. 7.3. 

В этом методе при вычислении величины шага распределение Больцмана заменяется на распределение Коши. Распределение Коши имеет, как показано на рис. 7.3, более длинные "хвосты", увеличивая тем самым вероятность больших шагов. В действительности, распределение Коши имеет бесконечную (неопределенную) дисперсию. С помощью такого простого изменения максимальная скорость уменьшения температуры становится обратно пропорциональной линейной величине, а не логарифму, как для алгоритма обучения Больцмана. Это резко уменьшает время обучения. Зависимость может быть выражена следующим образом:

Распределение Коши имеет вид

где есть вероятность шага величины

В данном уравнении может быть проинтегрирована стандартными методами. Решая относительно , получаем

где — коэффициент скорости обучения; — изменение веса.

Теперь применение метода Монте-Карло становится очень простым. Для нахождения x в этом случае выбирается случайное число из равномерного распределения на открытом интервале (необходимо ограничить функцию тангенса). Оно подставляется в формулу (5.7) в качестве , и с помощью текущей температуры вычисляется величина шага.