2. Математическое описание мпа
Математическое моделирование МПА следует выполнять на основе решения интегрального уравнения относительно двумерного распределения токов по плоскости антенны с ядром, зависящим от свойств материала подложки, такой подход является наиболее точным и реализован в ряде стандартных пакетах (MWOffice, Agilent и др.). Вместе с тем, существует ряд упрощенных подходов к расчету характеристик МПА, позволяющих с инженерной точностью оценить основные полевые характеристики. Одним из таких подходов является метод, разработанный Дернеридом, сводящийся к аналогии МПА и отрезку длинной линии, нагруженному с двух сторон на резистивные и емкостные элементы.
Резистивные
элементы эквивалентны потерям на
излучение, двух щелей с длиной равной
ширине МПА
,
расположенных на расстоянии равном
длине элемента
,
емкостные элементы описывают краевой
эффект (емкость между концом полосковой
линии передачи и проводящим основанием).
Резонансная частота
прямоугольной МПА
зависит от геометрии антенны (прежде
всего длины элемента L)
и диэлектрической проницаемости подложки
и определяется по формуле:
,
(1)
где с - скорость
света,
- так называемая эффективная диэлектрическая
проницаемость, которая отличается от
проницаемости материала подложки,
поскольку поле МПА присутствует как в
диэлектрике, так и в воздухе. Она
вычисляется по формуле:
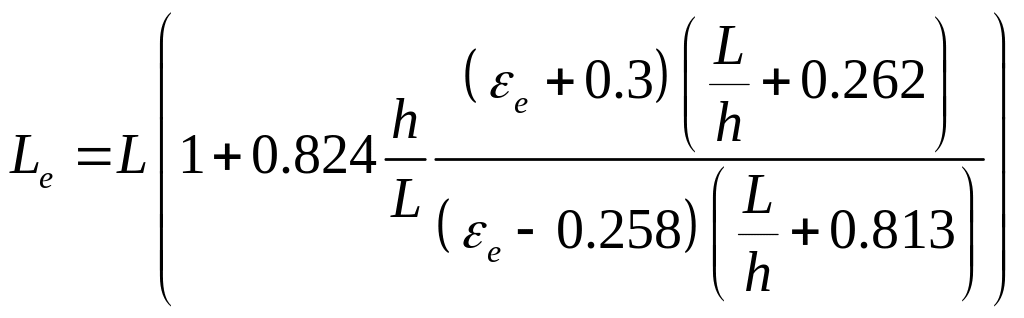
Здесь
-
диэлектрическая проницаемость материала
подложки, отн. ед.,
-
длина элемента,
-
толщина подложки.
Увеличение диэлектрической проницаемости подложки при фиксированной геометрии элемента приводит к понижению резонансной частоты. В ряде случаев в целях уменьшения габаритов антенных систем прибегают к использованию материалов подложки с относительной диэлектрической проницаемостью от 2 до 10. Одновременно с этим, уменьшение размеров МПА ведет к сужению полосы рабочих частот и уменьшению КНД.
Диаграмма
направленности МПА определяется как:
,
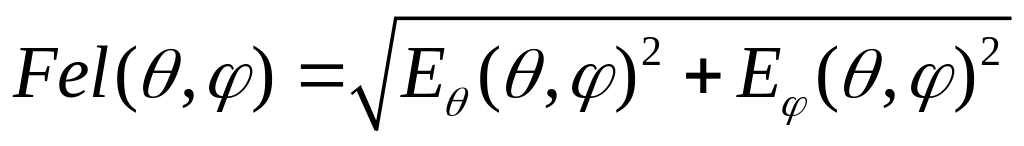где
и
- угломестная и азимутальная компоненты
поля излучения:
,
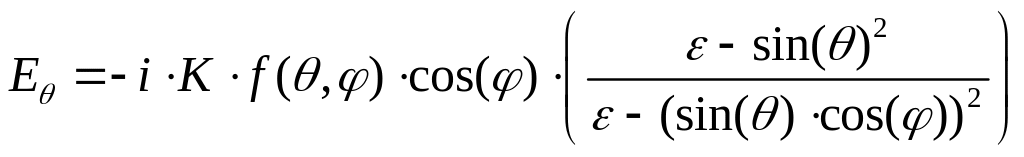(2)
,
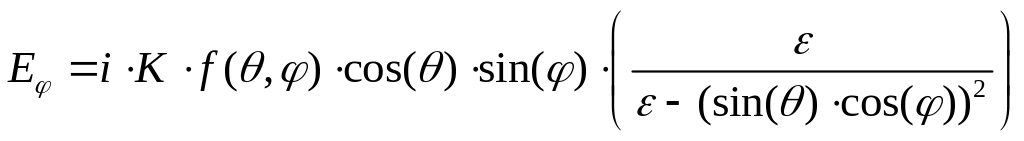здесь
-
угол места и азимутальный угол сферической
системы координат,
-
постоянная распространения,
-
длина волны в воздухе,
-
константа, зависящая
от амплитуды возбуждения,
-
ширина МПА.
Диаграмма
направленности антенной решетки
вычисляется в соответствии с теоремой
перемножения как произведение множителя
системы
на ДН одного элемента
:
(3)
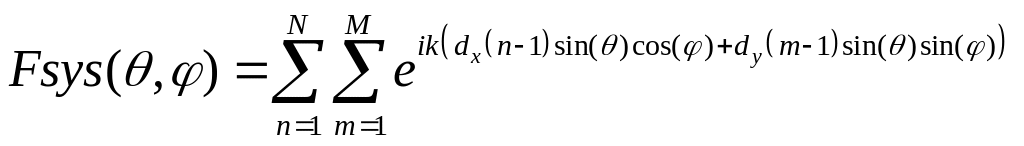(4)
где
- число элементов в решетке по одной и
другой координатам. (В данном случае
,
общее число
элементов в решетке равно произведению
),
- периоды антенной
решетки (т.е. расстояние между элементами)
по координатам х и у соответственно,
для исследуемой в работе АР
.
Лабораторный макет
В зависимости от режима измерения в лабораторной работе используются две схемы макета. На рис. 6. представлена схема лабораторного макета для измерения КСВ, на рис. 7. схема на основе которой проводятся исследования полевых характеристик.
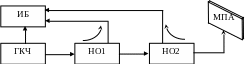
Рис. 6. Схема установки для измерения частотной зависимости КСВ.
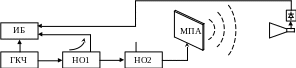
Рис. 7. Схема установки для измерения ДН.
Структура лабораторного макета аналогична используемой в работе №1, ее описание приводится на стр. .